Cô Mai Quỳnh – giáo viên đảm nhận bộ môn Toán tại Hệ thống Giáo dục Hocmai sẽ cung cấp phương pháp để tính chu vi và diện tích hình tam giác cũng như những dạng bài tập liên quan.
Trong chương trình Toán học lớp 3, học sinh đã bắt đầu được làm quen với hình tam giác thông qua dạng bài tập đếm hình cơ bản. Thế nhưng kể từ lớp 4 trở đi, kiến thức liên quan đến hình tam giác bắt đầu được mở rộng với những bài tập yêu cầu tính chu vi và diện tích. Việc nắm chắc được bản chất và những công thức quan trọng của hình tam giác sẽ giúp học sinh tự tin hơn khi tiếp cận với những dạng hình học khác sau này.
1. Khái quát về hình Tam giác
a) Khái niệm
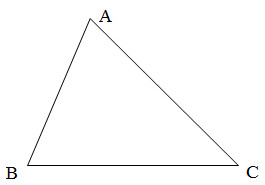
Hình tam giác là hình có 3 điểm , 3 cạnh và 3 góc với tổng số góc bằng 180o
b) Cấu tạo
3 điểm (A, B, C). 3 góc : (góc A, góc B, góc C)
3 cạnh (AB, AC, BC). Tổng số góc bằng 180°
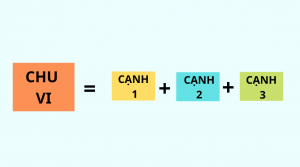
2. Chu vi tam giác
Chu vi của tam giác là tổng độ dài 3 cạnh của nó
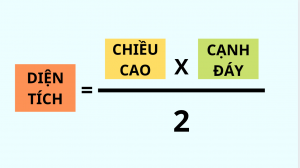
3. Diện tích tam giác
Muốn tính được diện tích của một tam giác thì bước đầu tiên học sinh phải xác định được đường cao của tam giác đó. Đường cao của tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được gọi là đáy ứng với đường cao. Độ dài của đường cao là khoảng cách giữa đỉnh và đáy.
 * Mẹo xác định đường cao bằng thước kẻ thẳng:
* Mẹo xác định đường cao bằng thước kẻ thẳng:
Dùng thước kẻ thẳng đặt vuông góc với cạnh đáy (vd: BC) (đặt sao cho cạnh nhỏ của thước kẻ trùng với cạnh đáy của hình tam giác ). Sau đó di chuyển thước kẻ cho đến khi đi qua đỉnh (vd: điểm A), trong lúc di chuyển, cạnh dưới thước kẻ vẫn trùng với đáy. Đường cao xác định được là đường thẳng AH nối từ điểm A và vuông góc với cạnh đáy BC.
a) Đường cao trong tam giác nhọn
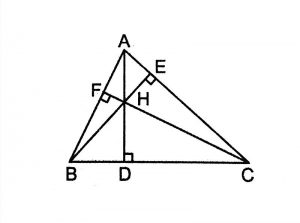
Trong tam giác nhọn ABC:
Đường cao AD tương ứng với đáy BC
Đường cao BE tương ứng với đáy AC
Đường cao CF tương ứng với đáy AB
Vậy diện tích của tam giác ABC là
SABC = (BC x AD) : 2 = (AC x BE) : 2 = (AB x CF) : 2
b) Đường cao trong tam giác vuông
Trong tam giác vuông, ta có sẵn hai đường cao của tam giác tương ứng với hai cạnh của góc vuông
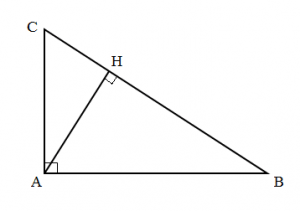
Trong tam giác ABC vuông tại A:
Đường cao AH tương ứng với đáy BC
Nếu coi AC là đường cao thì AB là đáy tương ứng và ngược lại
Vậy diện tích của tam giác ABC vuông tại đỉnh A là
SABC = (AB x AC) : 2 = (AH x BC) : 2
c) Đường cao trong tam giác tù
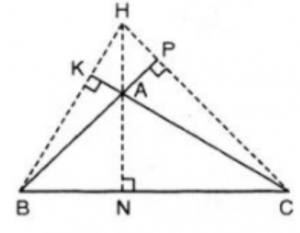
Trong tam giác tù ABC:
Đường cao AN tương ứng với đáy BC
Đường cao BK tương ứng với đáy AC
Đường cao CP tương ứng với đáy AB
Vậy diện tích của tam giác ABC là
SABC = (BC x AN) : 2 = (AC x BK) : 2 = (AB x CP) : 2
Từ việc xác định được chiều cao của từng loại tam giác, học sinh sẽ xây dựng được công thức tính diện tích cho mỗi loại tam giác khác nhau.
4. Các dạng bài tập thường gặp:
Dạng 1 : Tính độ dài cạnh khi biết chu vi của tam giác
Biết chu vi và hai cạnh, tìm cạnh còn lại
Lấy chu vi trừ tổng hai cạnh đã biết
Dạng 2: Tính độ dài cạnh hoặc chiều cao khi biết diện tích tam giác và yếu tố còn lại
Dựa vào công thức tính diện tích:
Diện tích = (cạnh đáy x chiều cao) : 2
Cạnh đáy = 2 x diện tích : chiều cao
Chiều cao = 2 x diện tích : cạnh đáy
Trên đây là toàn bộ phần nội dung về chu vi và diện tích của hình tam giác. Qua đó, cô Mai Quỳnh hy vọng học sinh nhận biết được những đặc điểm cơ bản của hình tam giác, công thức tính chu vi và diện tích cơ bản để từ đó mở rộng và ứng dụng vào từng loại tam giác khác nhau cũng như đối với các bài tập liên quan.
Để con học tập và ôn luyện toàn diện hơn, mời cha mẹ cùng tham khảo Chương trình Học Tốt: Các khóa học được xây dựng sát Chương trình chuẩn của Bộ Giáo Dục, đa dạng theo năng lực học của con. Phụ huynh sẽ được nhận tư vấn hoàn toàn miễn phí về khóa học ngay tại đây nhé!




















