[HM6 Toàn Diện] Bí quyết làm bài toán tìm hai số khi biết ẩn tổng và ẩn hiệu 

Cùng tìm hiểu phương pháp, bước thực hiện qua những bài tập cụ thể dưới đây.

 

Trong dạng toán tìm hai số khi biết tổng và hiệu thì ở mức độ nâng cao, đề bài thường đưa ra các dữ kiện dưới dạng ẩn tổng hoặc ẩn hiệu. Khi gặp phải bài toán này, học sinh cần phải mất thêm một vài bước làm để tìm ra được tổng và hiệu thông qua những kiến thức đã học. Tuy nhiên, ở một số trường hợp khó thì hai giá trị tổng hiệu đều bị ẩn đi. Nếu không biết cách làm thì học sinh dễ bị nhầm lẫn hoặc rơi vào trạng thái lúng túng, không biết phải bắt đầu từ đâu. Đối với dạng bài ở mức độ vận dụng, vận dụng cao này, thầy Bùi Minh Mẫn (Giáo viên Giải pháp luyện thi vào 6 toàn diện – HM6) sẽ hướng dẫn cho học sinh cách làm bài hiệu quả, từ đó nắm vững phương pháp tìm hai ẩn số trong bài toán và rèn luyện khả năng tư duy qua từng bài tập cụ thể.

Bài số 1: Tổng số thóc ở ba kho A, B, C là 450 tấn. Biết tổng số thóc ở cả hai kho B và C nhiều hơn số thóc kho A là 110 tấn và số thóc ở kho B chứa ít hơn kho C là 20 tấn. Tìm số thóc trong các kho A, B, C.

Hướng dẫn: Lập các dữ kiện trong đề bài ra thành phép tính.

Tổng số thóc ở ba kho A, B, C:

A + B + C = 450

=> (B + C) + A = 450 (1)

Tổng số thóc hai kho B và C nhiều hơn kho A là 110 tấn:

(B + C) – A = 110 (2)

=> (B + C) = 110 + A (3)

Số thóc kho B ít hơn kho C 20 tấn:

C – B = 20 (4)

Từ (1) và (2), học sinh có thể coi (B + C) là số lớn, A là số bé. Và tìm ra A. 

Từ (3) và (4), học sinh nhận ra B và C cũng tạo thành một tổng và một hiệu. Trong đó C là số lớn và B là số nhỏ. Dựa theo công thức, tính ra B và C.

Giải

Số thóc ở kho A là:

(450 – 110) : 2 = 170 (tấn thóc)

Tổng số thóc ở kho B và C là:

110 + 170 = 280 (tấn thóc)

Số thóc ở kho B là:

(280 – 20) : 2 = 130 (tấn thóc)

Số thóc ở kho C là:

130 + 20 = 150 (tấn thóc)

Đáp số: Kho A: 170 tấn; Kho B: 130 tấn; Kho C: 150 tấn

 

Bài số 2.Hai số có hiệu là 144, biết rằng nếu lấy số lớn chia cho số bé thì thương là 6 và số dư là 4. Tìm hai số đó.

Hướng dẫn: Thống kê các dữ kiện trên đề bài. Vẽ sơ đồ biểu diễn. 

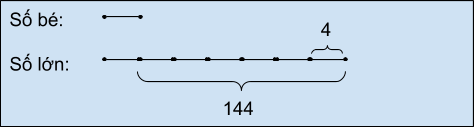
Số bé là 1 phần

Số lớn là 6 phần + 4 đơn vị

Số lớn – Số bé = 6 phần – 1 phần + 4 đơn vị = 5 phần + 4 đơn vị = 144

=> Tìm ra giá trị của một phần (Là số bé) và tìm số lớn.

Giải

Gọi số lớn là A, số bé là B.

Ta có: A – B = 144 (1)

Ngoài ra, số lớn chia số bé bằng 6 dư 4

A : B = 6 dư 4 => A = B x 6 + 4

Dựa theo sơ đồ trên,

Số bé là:

(144 – 4) : 5 = 28

Số lớn là:

28 + 144 = 172

Đáp số: Số lớn: 172; Số bé: 28

Bài 3. Bạn Bình có 22 viên bi gồm bi đỏ và bi xanh. Bình cho em 3 viên bi đỏ và 2 viên bi xanh. Bạn An lại cho Bình thêm 7 viên bi đỏ nữa. Lúc này, Bình có số bi đỏ gấp đôi số bi xanh. Hỏi lúc đầu Bình có bao nhiêu viên bi mỗi loại?

Hướng dẫn: Tóm tắt các dữ kiện trên bài theo dạng đơn giản

Gọi số bi đỏ của Bình là A, số bi xanh là B

A + B = 22

Sau khi cho em thì số bi Bình còn là:

(A – 3) + (B – 2) = 22 – (3 + 2)

Số bi Bình có sau khi An cho 7 viên bi đỏ là:

(A – 3 + 7) + (B – 2) = 22 – (3 + 2) + 7 = 24

Số bi đỏ gấp đôi số bi xanh, lập sơ đồ:

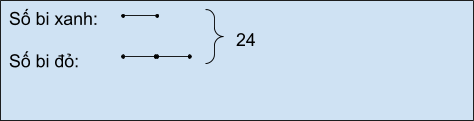
Từ đó tính toán được số bi đỏ và bi xanh Bình có.

Giải

Tổng số bi Bình có sau khi cho em và nhận của An là:

22 – (2 + 3) + 7 = 24 (viên)

Lúc này, số bi đỏ gấp đôi số bi xanh nên ta có sơ đồ: (như trên)

Ta thấy: Số bi xanh là 1 phần, số bi đỏ là 2 phần. Tổng 3 phần có giá trị bằng 24. Vậy, giá trị của một phần là:

24 : 3 = 8 

Giá trị 1 phần cũng là số viên bi xanh, nên số bi xanh là 8 viên.

Số bi xanh của Bình lúc đầu là:

8 + 2 = 10 (viên)

Số bi đỏ của Bình lúc đầu là:

(8 x 2) + 3 – 7 = 12 (viên)

Đáp số: Bi xanh: 10 viên; Bi đỏ: 12 viên

Bài 4. Hai bể nước chứa tất cả 5000 lít nước. Người ta mở vòi để xả nước ra ngoài thì mỗi phút bể thứ nhất chảy ra 25 lít, ở bể thứ hai chảy ra 35 lít. Sau nửa giờ thì đóng vòi lại. Khi đó số nước còn lại ở hai bể bằng nhau. Hỏi lúc đầu hai bể chứa bao nhiêu lít nước?

Hướng dẫn

Giải

Đổi: nửa giờ = 30 phút

Sau nửa giờ, bể thứ nhất chảy ra được số lít nước là:

25 x 30 = 750 (lít)

Sau nửa giờ, bể thứ hai chảy ra được số lít nước là:

35 x 30 = 1050 (lít)

Hiệu số lít hai bể là:

1050 – 750 = 300 (lít)

Số lít nước trong bể thứ nhất là:

(5000 – 300) : 2 = 2350 (lít)

Số lít nước trong bể thứ hai là:

5000 – 2350 = 2650 (lít)

Đáp số: Bể thứ nhất: 2350 lít; Bể thứ hai: 2650 lít

 

Bài số 5. An có 165 viên bi để vào hai túi. An lấy ở túi phải sang cho túi trái một số bi bằng số bi ở túi trái, sau đó lại lấy ở túi trái sang cho túi phải một số bi bằng số bi còn lại ở túi phải. Lúc này số bi ở túi phải hơn số bi ở túi trái 135 viên. Lúc đầu, túi phải có bao nhiêu viên?

Hướng dẫn: Tóm tắt dữ kiện

Gọi số bi ở túi phải là A, túi trái là B

A + B = 165

Chuyển một số bi từ túi phải sang túi trái bằng số bi túi trái => số bi túi phải lớn hơn số bi túi trái. Sau khi chuyển, số bi trong hai túi là:

(A – B) + (B + B) = 165

Túi phải: A – B

Túi trái: B + B

Tiếp tục, lấy ở túi trái sang cho túi phải một số bi bằng số bi còn lại ở túi phải thì số bi trong hai túi thay đổi như sau:

Túi phải: (A – B) + (A – B) = 2 (A + B)

Túi trái: (B + B) – (A – B) = 3B – A

Lúc này, số bi túi phải hơn túi trái 135 viên.

Giải

Sau lần chuyển thứ hai, số bi túi phải là:

(165 + 135) : 2 = 150 (viên)

Sau lần chuyển thứ nhất, số bi túi phải là:

150 : 2 = 75 (viên)

Sau lần chuyển thứ nhất, số bi túi trái là:

165 – 75 = 90 (viên)

Lúc đầu, túi trái có số bi là:

90 : 2 = 45 (viên)

Lúc đầu, túi phải có số bi là:

165 – 45 = 120 (viên)

Đáp số: Túi phải: 120 viên; Túi trái: 45 viên

Bài toán “Tìm hai số khi biết ẩn tổng và ẩn hiệu” là dạng khó, với nhiều bước tính phức tạp, lắt léo. Qua 5 bài tập minh họa, học sinh có thể thấy, không dễ dàng để tìm ra được tổng và hiệu ẩn sau các dữ kiện có sẵn của đề bài. Có những trường hợp, học sinh có thể suy luận tuy nhiên với những bài như này, các em nên cố gắng đưa về sơ đồ biểu diễn thành các phần. Khi ghép các dữ kiện vào trong sơ đồ, phép tính sẽ trở nên đơn giản, qua đó tìm kiếm giá trị cần tìm dễ dàng.

Với mức độ vận dụng, vận dụng cao như bài tập trên, học sinh có thể gặp trong các đề thi vào 6 trường tốp đầu. Chính vì vậy, các em cần đặc biệt lưu ý và cố gắng luyện giải càng nhiều càng tốt. Luyện tập càng nhiều, tự nhiên sẽ hình thành phản xạ khi gặp phải, có nhiều hướng tư duy, suy luận để giải bài hơn, từ đó tìm ra cách giải quyết nhanh hơn. Đặc biệt, trong Giải pháp luyện thi vào 6 toàn diện – HM6, những dạng bài phức tạp như “Tìm hai số khi biết ẩn tổng và ẩn hiệu” rất nhiều, học sinh dễ dàng được thực hành, vận dụng kiến thức.

Ngoài ra, khi gặp bất cứ kiến thức, bước giải nào không hiểu, học sinh cũng sẽ nhận được sự hỗ trợ nhanh chóng từ đội ngũ giáo viên, biên tập viên chuyên sâu của Giải pháp HM6. Quá trình ôn thi hiệu quả chính là khi các em có thể học, ôn, luyện, hỏi và kiểm tra đánh giá năng lực đúng đắn. Tiếp xúc kiến thức, ôn tập hệ thống lại theo chủ đề, luyện giải những bài tập từ thông hiểu đến vận dụng cao, thắc mắc những điều khó khăn trong quá trình học tập và thực hành đánh giá hiểu quả sau một chu trình ôn luyện. Tất cả những điều trên đều được HM6 tổng kết trọn vẹn trong bộ giải pháp 3 môn Toán – Tiếng Việt – Tiếng Anh. 

Đừng chần chừ khi sử dụng người bạn đồng hành này để tự chủ động hoàn thiện các kĩ năng làm bài tập, ôn thi tại nhà của mình nhé! 

Đăng ký Giải pháp luyện thi toàn diện vào 6 – HM6 TẠI ĐÂY