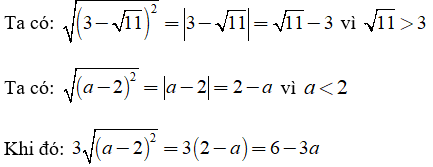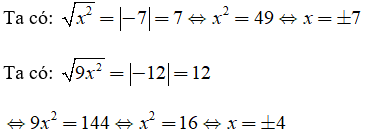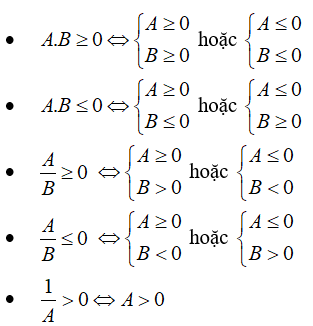Home Kiến thức 9 thi vào 10 Căn bậc 2 và hằng đẳng thức – Toán lớp 9

Căn bậc 2 và hằng đẳng thức – Toán lớp 9

16/06/2022

5537

A. Lý thuyết căn bậc 2 và hằng đẳng thức

I. CĂN THỨC BẬC HAI

1. Định nghĩa căn thức bậc 2

Cho A là 1 biểu thức đại số xác định, ta gọi √A là căn thức bậc hai của A và A được gọi là biểu thức lấy căn hay còn có tên gọi khác là biểu thức dưới dấu căn.

2. Điều kiện để một căn thức bậc 2 có nghĩa (hay có nghĩa)

Điều kiện của một biểu thức có căn thức bậc 2 có nghĩa khi vào chỉ khi biểu thức đó lớn hơn hoặc bằng 0.

√A xác định (có nghĩa) ⇔ A ≥ 0

3. Một số ví dụ minh họa

Tìm điều kiện để √3x có nghĩa

Hướng dẫn giải: Để √3x có nghĩa ⇔ 3x ≥ 0 ⇔ x ≥ 0.

Tìm điều kiện của √(3 – 7x)

Hướng dẫn giải: Để √(3 – 7x) ⇔ 3 – 7x ≥ 0 ⇔ x ≤ 3/7.

Tìm điều kiện của √(2 – 3x)

Hướng dẫn giải: Để √(2 – 3x) ⇔ 2 – 3x ≥ 0 ⇔ x ≤ 2/3.

Tìm điều kiện để √(x – 6)

Hướng dẫn giải: Để √(x – 6) ⇔ x – 6 ≥ 0 ⇔ x ≥ 6.

II. HẰNG ĐẲNG THỨC

Để có thể khai căn một biểu thức, ta sử dụng hằng đẳng thức sau:

√(A²) = |A|

Bài tập 1: Rút gọn biểu thức sau với điều kiện a < 2

HM10 2024 - GIẢI PHÁP LUYỆN THI TOÀN DIỆN

NẮM CHẮC KIẾN THỨC - KHÔNG LO BIẾN DỘNG ĐỀ THI

Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP

Ưu đãi đặt chỗ sớm - Giảm đến 45%! Áp dụng cho PHHS đăng ký trong tháng này!

TOPCLASS 2024 - CHƯƠNG TRÌNH HỌC TOÀN DIỆN

NẮM CHẮC KIẾN THỨC - BỨT PHÁ ĐIỂM SỐ

Chu trình học tập khép kín HỌC - LUYỆN - HỎI - KIỂM TRA
Đa dạng hình thức học - Phù hợp với mọi nhu cầu
Đội ngũ giáo viên giảng dạy nổi tiếng với 16+ năm kinh nghiệm
Dịch vụ hỗ trợ học tập đồng hành xuyên suốt quá trình học tập

Ưu đãi đặt chỗ sớm - Giảm đến 45%! Áp dụng cho PHHS đăng ký trong tháng này!

Giải:

Bài tập 2: Tìm x với điều kiện sau:

Giải:

III. MỘT SỐ KIẾN THỨC CẦN LƯU Ý VỀ CĂN BẬC 2 VÀ HẰNG ĐẲNG THỨC

1. Giá trị tuyệt đối

• Định nghĩa:

|A| nhận 2 giá trị trong các trường hợp sau:

– |A| = A ⇔ A ≥ 0

– |A| = -A ⇔ A < 0

• Một số hệ quả của giá trị tuyệt đối

– |A| ≥ 0 với mọi A A

– |A| = |-A|

– |A| = |B| ⇔ A = B hoặc A = -B

– |A| = A ⇔ A ≥ 0; |A| = -A ⇔ A ≤ 0; |A| = 0 ⇔ A = 0

2. Dấu của một tích, dấu của một thương

B. MỘT SỐ DẠNG BÀI THƯỜNG GẶP

DẠNG 1: Tìm điều kiện để một để một căn thức bậc hai xác định.

• Tìm điều kiện để căn thức xác định: √A có nghĩa (hay căn bậc 2 được xác định) ⇔ A ≥ 0

• Giải bất phương trình điều kiện A ≥ 0

• Kết luận đáp án

DẠNG 2: Tính giá trị của một biểu thức chứa căn – Khai căn của biểu thức

• Sử dụng hằng đẳng thức √(A2) = |A| để tiến hành khai căn

• Rút gọn biểu thức đã cho và tính giá trị của biểu thức chứa căn

DẠNG 3: Giải bài tập bằng phương pháp phân tích đa thức thành nhân tử

• Viết A ≥ 0 thành dạng (√A)2

• Áp dụng các công thức để tiến hành phân tích đa thức thành nhân tử
+ A² – B² = (A – B)(A + B)
+ A² ± 2AB + B² = (A ± B)²

• Trông quá trình phân tích thành nhân tử có thể thêm, bớt các thành phần khác để phục vụ cho việc triển khai công thức

DẠNG 4: Giải phương trình chưa căn thức bậc 2

• Tiến hành khai căn

• Giải phương trình chứa dấu giá trị tuyệt đối

• Sử dụng các công thức để phân tích thành nhân tử rồi tiến hành giải

Tham khảo thêm:

Tổng hợp kiến thức toán lớp 9

Căn bậc 2 lớp 9

Tài liệu ôn tập toán 9