Sau những tuần học đầu tiên, nhiều khu vực và tỉnh thành cũng bắt đầu bước vào giai đoạn thi giữa kỳ để kiểm tra đánh giá kiến thức và kỹ năng của học sinh vì vậy việc ôn tập và nắm vững kiến thức trọng tâm là một điều vô cùng quan trọng. Dưới đây là tổng hợp những kiến thức toán lớp 6 những tuần đầu để giúp học sinh có thể dễ dàng hơn trong việc ôn luyện và nắm bắt kiến thức hơn.
A. Tập hợp
1. Khái niệm tập hợp và phần tử của tập hợp
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định. Chúng được gọi là những phần tử của tập hợp đó.
x là phần tử của tập hợp A ký hiệu là x ∈ A ( đọc là x thuộc A)
Y không là phần tử của tập hợp A ký hiệu là y ∉ A (đoc là y không thuộc A )
Chú ý: Khi x thuộc A, ta còn nói “x nằm trong A”, hay “A chứa x”.
2. Các kí hiệu
– Người ta thường dùng các chữ in hoa A, B, C ,… để kí hiệu tập hợp, các chữ in thường a, b, c,… để kí hiệu phần tử của tập hợp.
– Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn , cách nhau bởi dấu phẩy “,” hoặc dấu chấm phẩy “;” (đối với trường hợp các phần tử là số).
– Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
– Phần tử x thuộc tập hợp A được kí hiệu là x A , đọc là “x thuộc A”. Phần tử y không thuộc tập hợp A được kí hiệu là y A , đọc là “y không thuộc A”.
– Tập hợp không chứa phần tử nào gọi là tập rỗng, kí hiệu là Ø
Chú ý. Ta viết n ∈ N có nghĩa n là một số tự nhiên.
3. Cách cho tập hợp
Để cho một tập hợp, thường có hai cách:
a) Liệt kê các phần tử của tập hợp.
b) Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp. Ngoài hai cách trên, người ta còn minh họa tập hợp bằng một vòng kín, mỗi phần tử của tập hợp được biểu diễn bởi một dấu chấm bên trong vòng kín đó. Ta nói tập hợp được minh họa bằng sơ đồ Venn.
B. Tập hợp các số tự nhiên
1. Tập hợp N và tập hợp N*
Các số 0; 1; 2; 3;… là các số tự nhiên
Tập hợp các số tự nhiên được ký hiệu là N
N = {0;1;2;3;4;5}
Tập hợp các số tự nhiên khác không được gọi là N*
N*= {1;2;3;4;5}
2. Cách đọc và viết số tự nhiên
Khi viết các số tự nhiên có từ bốn chữ số trở lên, người ta thường viết tách riêng từng nhóm ba chữ số kể từ phải sang trái cho dễ đọc.
Chú ý: Một nghìn triệu bằng một tỉ. Ngoài ra, hàng tỉ, hàng chục tỉ, hàng trăm tỉ hợp thành lớp tỉ
3. Thứ tự trong tập hợp số tự nhiên:
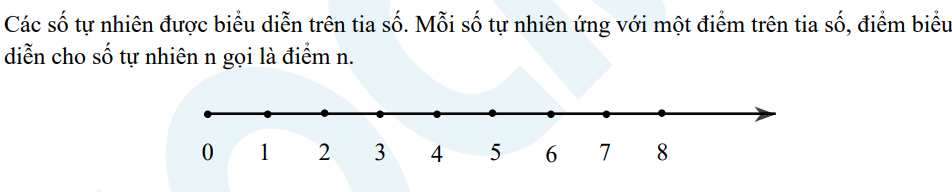
Trong hai số tự nhiên a và b khác nhau, có một số nhỏ hơn số kia. Nếu số a nhỏ hơn số b ta viết a < b ( a nhỏ hơn b). Ta cũng nói số b lớn hơn số a và viết b > a
Khi biểu diễn trên tia số nằm ngang có chiều mũi tên đi từ trái sang phải, nếu a b thì điểm a nằm bên trái điểm b.
Ta biết a b khi a nhỏ hơn b hoặc a = b, b a để chỉ b > a hoặc b = a
Mỗi số tự nhiên có một số liền sau cách nó một đơn vị. Hai số đó được gọi là hai số tự nhiên liên tiếp
Tính chất bắc cầu: Nếu a < b mà b < c thì a < c.
Với số tự nhiên a cho trước:
– Ta viết: x ≤ a, để chỉ x < a hoặc x = a.
– Ta viết: x ≥ a, để chỉ x > a hoặc x = a
4. Ghi số tự nhiên
Số tự nhiên được viết trong hệ thập phân bởi một, hai hay nhiều chữ số. Các chữ số được dùng là0;1;2;3;4;5;6;7;8;9. Khi một số gồm hai chữ số trở lên thì chữ số đầu tiên (tính từ trái sang phải) khác 0.
Khi viết các số tự nhiên có từ 4 chữ số trở lên, ta nên viết tách riêng từng nhóm ba chữ số kể từ phải sang trái cho dễ đọc.
Trong cách viết một số tự nhiên có nhiều chữ số, mỗi chữ số ở những vị trí khác nhau có giá trị khác nhau.

5. So sánh hai số tự nhiên
– Trong hai số tự nhiên có số chữ số khác nhau: Số nào có nhiều chữ số hơn thì lớn hơn, số nào có ít chữ số hơn thì nhỏ hơn.
– Để so sánh hai số tự nhiên có số chữ số bằng nhau, ta lần lượt so sánh từng cặp chữ số trên cùng một hàng (tính từ trái sang phải), cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số tự nhiên chứa chữ số đó lớn hơn.
6. Hệ La Mã
Ngoài cách ghi số trong hệ thập phân gồm các chữ số từ 0 đến 9 và các hàng (đơn vị, chục, trăm, nghìn, …) như trên, còn có cách ghi số La Mã như sau:
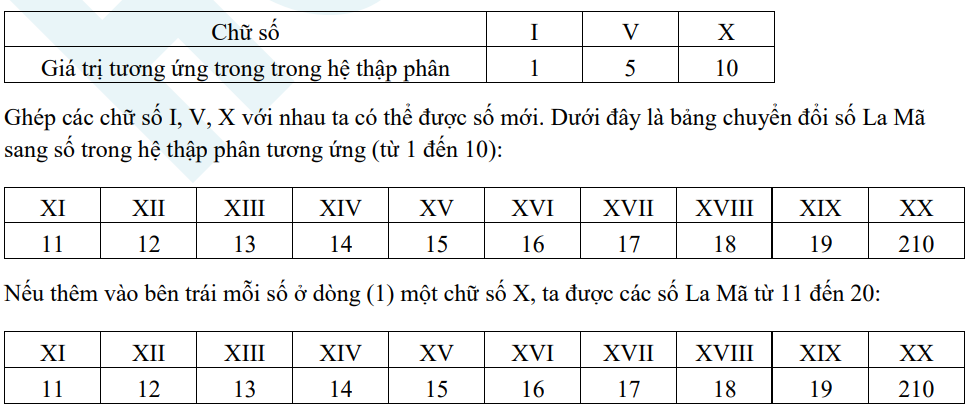

c. Phép cộng, phép trừ các số tự nhiên
1. Phép cộng
Phép cộng các số tự nhiên: a + b = c.
Trong đó: a và b là các số hạng, c là tổng Phép cộng các số tự nhiên có tính chất giao hoán, kết hợp, cộng với số 0.
Cụ thể:
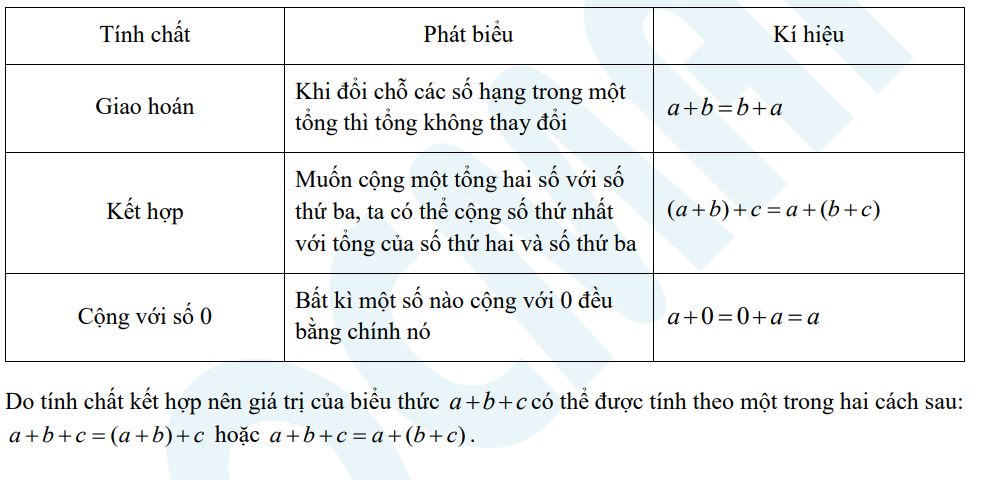
2. Phép trừ
Phép trừ một số tự nhiên cho một số tự nhiên nhỏ hơn hoặc bằng nó: a – b = c ( a ≥ b)
Trong đó: a là số bị trừ, b là số trừ, c là hiệu.
Nếu a – b = c thì a = b+ c
Nếu a + b = c thì a = c – b và b = c – a
D. Phép nhân, Phép chia các số tự nhiên
1. Phép nhân:
Phép nhân các số tự nhiên: a x b = c , trong đó a, b là các thừa số, c là tích.
Quy ước:
– Trong một tích, ta có thể thay dấu nhân “x” bằng dấu chấm “.”.
– Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một thừa số bằng số, ta có thể không cần viết dấu nhân giữa các thừa số.
a) Nhân hai số có nhiều chữ số
Sau khi đặt tính ta thực hiện theo các bước sau:
– Tính tích riêng thứ nhất: Ta lấy chữ số hàng đơn vị của số phía bên dưới nhân với số bên trên lần lượt theo thứ tự từ phải sang trái.
– Tính tích riêng thứ hai: Lấy chữ số hàng chục của số bên dưới nhân với số bên trên theo thứ tự từ phải sang trái. Tích này viết lùi sang bên trái một cột so với tích riêng thứ nhất.
– Tính tích riêng thứ ba: Lấy chữ số hàng trăm của số bên dưới nhân với số bên trên theo thứ tự từ phải sang trái. Tích này viết lùi sang bên trái hai cột so với tích riêng thứ nhất.
– Cộng các tích riêng theo cột dọc, ta được tích hai số có nhiều chữ số cần tìm.
b) Tính chất của phép nhân
Phép nhân các số tự nhiên có các tính chất sau:
– Giao hoán: a.b = b.a
– Kết hợp: (a.b).c = a.(b.c)
– Nhân với số 1: a.1 = 1.a = a
– Phân phối đối với phép cộng và phép trừ:
a.(b+c) = a.b + a.c
a.(b-c) = a.b – a.c
Do tính chất kết hợp nên giá trị của biểu thức a.b.c có thể được tính theo một trong hai cách sau:
a.b.c = (a.b).c hoặc a.b.c = a.(b.c)
2. Phép chia
a) Phép chia hết
Phép chia một số tự nhiên cho một số tự nhiên khác 0: a:b = q ( b≠0)
Trong đó: a là số bị chia, b là số chia, q là thương.
– Nếu a : b = q thì a = b.q .
– Nếu a : b = q, q≠0 thì a : q = b
b) Phép chia có dư
Cho hai số tự nhiên a và b với b0, Khi đó luôn tìm được đúng hai số tự nhiên q và r sao cho
a = b.p + r, trong đó 0 r < b
– Khi r = 0 ta có phép chia hết.
– Khi r ≠ 0 ta có phép chia có dư. Ta nói a chia cho b được thương là q và số dư là r. Kí hiệu
a : b = q ( dư r)
E. Phép lũy thừa với số mũ tự nhiên
1. Lũy thừa
Đối với tích của nhiều thừa số bằng nhau ta có thể viết gọn thành một lũy thừa.
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa.

2. Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ![]()
3. Chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ:
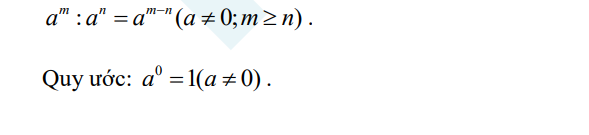
F. Thứ tự thực hiện các phép tính:
1. Thứ tự thực hiện các phép tính trong biểu thức không chứa dấu ngoặc
– Khi biểu thức chỉ có các phép tính cộng và trừ (hoặc chỉ có các phép tính nhân và chia), ta thực hiện phép tính theo thứ tự từ trái sang phải.
Khi biểu thức có các phép tính cộng, trừ, nhân, chia, ta thực hiện phép tính nhân và chia trước, rồi đến cộng và trừ.
Khi biểu thức có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép tính nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.
2. Thứ tự thực hiện các phép tính trong biểu thức chứa dấu ngoặc
Khi biểu thức có chứa dấu ngoặc, ta thực hiện các phép tính trong dấu ngoặc trước.
Nếu biểu thức có các dấu ngoặc tròn (), ngoặc vuông [], ngoặc nhọn{} , ta thực hiện phép
tính trong dấu ngoặc tròn trước, rồi thực hiện phép tính trong dấu ngoặc vuông, cuối cùng thực hiện phép tính trong dấu ngoặc nhọn: ()→[]→{}
G. Quan hệ chia hết, tính chất chia hết
1. Quan hệ chia hết
a. Khái niệm về chia hết

b. Cách tìm bội và ước của 1 số
Để tìm các bội của n ( n ∈ N*), ta có thể lần lượt nhân n với 0, 1, 2, 3,…. Khi đó các kết quả nhận được đều là bội của n
Để tìm ra các ước của số tự nhiên n lớn hơn 1, ta có thể lần lượt chia n cho các số tự nhiên từ 1 đến n. Khi đó các phép chia hết cho ta số chia là ước của n.
Ta kí hiệu Ư(a) là tập hợp các ước của a và B(b) là tập hợp các bội của b.
2. Tính chất chia hết
a. Tính chất chia hết của một tổng
Nếu tất cả các số hạng của tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

b. Tính chất chia hết của một hiệu
Nếu số bị trừ và số trừ đều chia hết cho cùng một số thì hiệu chia hết cho số đó

c. Tính chất chia hết của một tích
Nếu một thừa số của tích chia hết cho một số thì tích chia hết cho số đó.

H. Dấu hiệu chia hết cho 2, cho 5
1. Dấu hiệu chia hết cho 2
Các số có chữ số tận cùng là; 0, 2, 4, 6, 8 (tức là số chẵn) thì chia hết cho 2 và chỉ những số đó
mới chia hết cho 2.
2. Dấu hiệu chia hết cho 5
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
I. Dấu hiệu chia hết cho 3, cho 9
1. Dấu hiệu chia hết cho 3
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
2. Dấu hiệu chia hết cho 9
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
K. Số nguyên tố, Hợp Số
Số nguyên tố. Hợp số
Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.
– Số 0 và số 1 không là số nguyên tố cũng không là hợp số.
– Để chứng tỏ số tự nhiên a lớn hơn 1 là một hợp số, ta chỉ cần tìm một ước của a khác 1 và khác a.
– Nếu số nguyên tố p là ước của số tự nhiên a thì p được gọi là ước nguyên tố của a.
L. Phân tích một số ra thừa số nguyên tố
1. Cách tìm một ước nguyên tố của một số
Để tìm một ước nguyên tố của số a ta có thể làm như sau: Lần lượt thực hiện phép chia a cho các số
nguyên tố theo thứ tự tăng dần 2, 3, 5, 7, 11, 13, …
Khi đó phép chia hết đầu tiên cho ta số chia là một ước nguyên tố của a.
2. Phân tích một số ra thừa số nguyên tố
Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Ta nên chia mỗi số cho ước nguyên tố nhỏ nhất của nó.
Cứ tiếp tục chia như thế cho đến khi được thương là 1.
Có hai phương pháp phân tích một số ra thừa số nguyên tố: Phương pháp phân tích theo sơ đồ cây và phương pháp phân tích theo sơ đồ cột.
Chú ý:
– Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố.
– Mỗi số nguyên tố chỉ có một dạng phân tích ra thừa số nguyên tố là chính số đó.
– Có thể viết gọn dạng phân tích một số ra thừa số nguyên tố bằng cách dùng lũy thừa.
– Thông thường, khi phân tích một số tự nhiên ra thừa số nguyên tố, các ước nguyên tố được viết theo thứ tự tăng dần.
– Người ta quy ước dạng phân tích ra thừa số nguyên tố của một số nguyên tố là chính nó.
– Ngoài cách làm như trên, ta cũng có thể phân tích một số ra thừa số nguyên tố bằng cách viết số đó thành tích của hai thừa số một cách linh hoạt.
Nhận xét:
Dù phân tích một số ra thừa số nguyên tố bằng cách nào thì cuối cùng ta cũng được cùng một kết quả.
M. Ước chung và ước chung lớn nhất
1. Ước chung và ước chung lớn nhất
Số tự nhiên n được gọi là ước chung của hai số a và b nếu n vừa là ước của a vừa là ước của b.
Số lớn nhất trong các ước chung của a và b được gọi là ước chung lớn nhất của a và b.
Quy ước: Viết tắt ước chung là ƯC và ước chung lớn nhất là ƯCLN.
Ta kí hiệu: Tập hợp các ước chung của a và b là ƯC(a,b); ước chung lớn nhất của a và b là
ƯCLN(a, b).
ƯC(a,b) là một tập hợp, ƯCLN(a, b) là một số.

Nhận xét:
– Trong các số đã cho, nếu số nhỏ nhất là ước của các số còn lại thì WCLN của các số đã cho chính là số nhỏ nhất ấy.

Chú ý:
Số tự nhiên n được gọi là ước chung của ba số a, b, c nếu n là ước của cả ba số a, b, c.
Ước chung của hai số là ước của ước chung lớn nhất của chúng.
Để tìm ước chung của các số, ta có thể làm như sau:
– Tìm ƯCLN của các số đó.
– Tìm các ước của ƯCLN đó.
2. Tìm ước chung lớn nhất bằng cách phân tích ra thừa số nguyên tố
Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố
Bước 1. Phân tích mỗi số ra thừa số nguyên tố.
Bước 2. Chọn ra các thừa số nguyên tố chung, mỗi thừa số lấy với số mũ nhỏ nhất.
Bước 3. Lấy tích của các lũy thừa đã chọn, ta nhận được ước chung lớn nhất cần tìm.
Chú ý:

3. Hai số nguyên tố cùng nhau
Hai số nguyên tố cùng nhau là hai số có ước chung lớn nhất bằng 1.
Phân số tối giản là phân số có tử và mẫu là hai số nguyên tố cùng nhau.
N. Bội chung nhỏ nhất
1. Bội chung và bội chung nhỏ nhất
Số tự nhiên n được gọi là bội chung của hai số a và b nếu n vừa là bội của a vừa là bội của b.
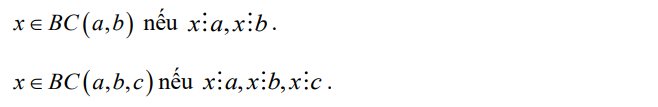
Số nhỏ nhất khác 0 trong các bội chung của a và b được gọi là bội chung nhỏ nhất của a và b.
Quy ước: Viết tắt bội chung là BC và bội chung nhỏ nhất là BCNN.
Ta kí hiệu: Tập hợp các bội chung của a và b là BC(a, b); bội chung nhỏ nhất của a và b là
BCNN(a, b)

2. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố
Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố:
Bước 1. Phân tích mỗi số ra thừa số nguyên tố.
Bước 2. Chọn ra các thừa số nguyên tố chung và các thừa số nguyên tố riêng, mỗi thừa số lấy với số mũ lớn nhất.
Bước 3. Lấy tích của các lũy thừa đã chọn, ta nhận được bội chung nhỏ nhất cần tìm.
3. Tìm bội chung từ bội chung nhỏ nhất
Để tìm bội chung của các số đã cho ta có thể làm như sau:
Bước 1. Tìm BCNN của các số.
Bước 2. Tìm các bội của BCNN đó.
4. Ứng dụng của bội chung nhỏ nhất
– Để quy đồng mẫu hai phân số ab và cd, ta phải tìm mẫu chung của hai phân số đó. Thông thường ta nên chọn mẫu chung là bội chung nhỏ nhất của hai mẫu.
– Để tính tổng (hiệu) các phân số không cùng mẫu, ta có thể làm như sau:
Bước 1. Chọn mẫu chung là BCNN của các mẫu
Bước 2. Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu)
Bước 3. Sau khi nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng, ta cộng (trừ) các phân số có cùng mẫu Bội chung nhỏ nhất của hai số nguyên tố cùng nhau bằng tích của hai số đó.




















