Phép cộng là một trong bốn phép tính quan trọng nhất của cấp Tiểu học: Phép cộng, phép trừ, phép nhân, phép chia. Tuy nhiên, khi lên lớp 3, các em học sinh sẽ được học phép cộng ở mức độ khó hơn với những con số phức tạp hơn. Hãy cùng theo dõi bài giảng của cô Nguyễn Thị Huệ (Hocmai Tiểu học) để khám phá chủ đề toán này nhé!
Xem đồng hồ và cách giải những bài toán liên quan (phần 1)
Khác với lớp 1 và 2, chỉ tập trung vào các kiến thức để các em học sinh bắt đầu làm quen với môn Toán thì từ lớp 3 trở đi, chương trình học được mở rộng và mang tính vận dụng cao hơn. Đặc biệt là môn toán khi bài tập trở nên phức tạp và yêu cầu sự tư duy nhiều. Phép cộng cũng vậy.
Sẽ có 2 loại phép cộng mà học sinh được làm quen từ đầu năm học. Đó là phép cộng có nhớ và phép cộng không nhớ!
Khái niệm phép cộng có nhớ và phép cộng không nhớ
| Phép cộng CÓ NHỚ | Phép cộng KHÔNG CÓ NHỚ |
| 35 + 8 = 43
Ta có: 5 cộng 8 bằng 13, viết 3 nhớ 1 3 cộng 0 bằng 3, nhớ 1 bằng 4 Vậy kết quả bằng 43 Trong đó:
|
30 + 5 = 35
Ta có: 0 cộng 5 bằng 5, viết 5 3 cộng 0 bằng 3, viết 3 Vậy kết quả bằng 35 Trong đó:
|
| Phép cộng có nhớ là các phép cộng mà khi cộng dồn các số hạng thuộc một hàng nào đó lại thì có kết quả lớn hơn 10. | Phép cộng không có nhớ là các phép cộng mà khi cộng dồn các số hạng thuộc một hàng nào đó lại thì có kết quả bé hơn 10. |
Các bài tập liên quan tới phép cộng không có nhớ

(Cô Nguyễn Thị Huệ giảng bài về phép cộng không có nhớ)
Để xem bài giảng đầy đủ, quý phụ huynh và các em học sinh hãy truy cập vào đường link dưới đây nhé: https://hocmai.vn/bai-giang-truc-tuyen/72468/bai-01-phep-cong-khong-nho.html
Dạng 1: Tính nhẩm.
Bài 1: Tính nhẩm.
Quy tắc:
– Đánh giá các số hạng trong phép tính xem có điểm gì đặc biệt (đều có hàng đơn vị bằng 0, hoặc hàng chục và hàng đơn vị bằng 0,…)
– Từ đó, thực hiện phép tính cộng như thường.
Ví dụ: 10 + 20 + 30 = ?
Hàng đơn vị của cả ba số trong phép tính này là chữ số 0, nên chỉ cần quan tâm tới các chữ số hàng chục.
Ta có: 1 + 2 + 3 = 6, viết 6.
Sau đó, viết số 0 vào sau số 6.
Kết quả của phép tính là: 60
Bài 2: Viết 3 số tiếp theo vào dãy số.
Quy tắc:
– Tìm quy tắc của dãy số (tăng dần, giảm dần)
– Tìm quy tắc của các số trong dãy số (tăng, giảm bao nhiêu đơn vị)
– Từ đó, tìm ra các số còn thiếu và điền vào chỗ trống.
Ví dụ: 10; 20; 30; 40; …; ….; …;
Nhận xét: Đây là một dãy số tăng dần bởi vì từ số thứ 2 trong dãy, sẽ bằng số liền trước nó cộng thêm 10.
Ta có: 20 = 10 + 10
30 = 20 + 10
Nên số liền ngay sau 40 sẽ là 40 + 10 = 50
Làm tương tự với các số còn lại ta sẽ được dãy số: 10; 20; 30; 40; 50; 60; 70.
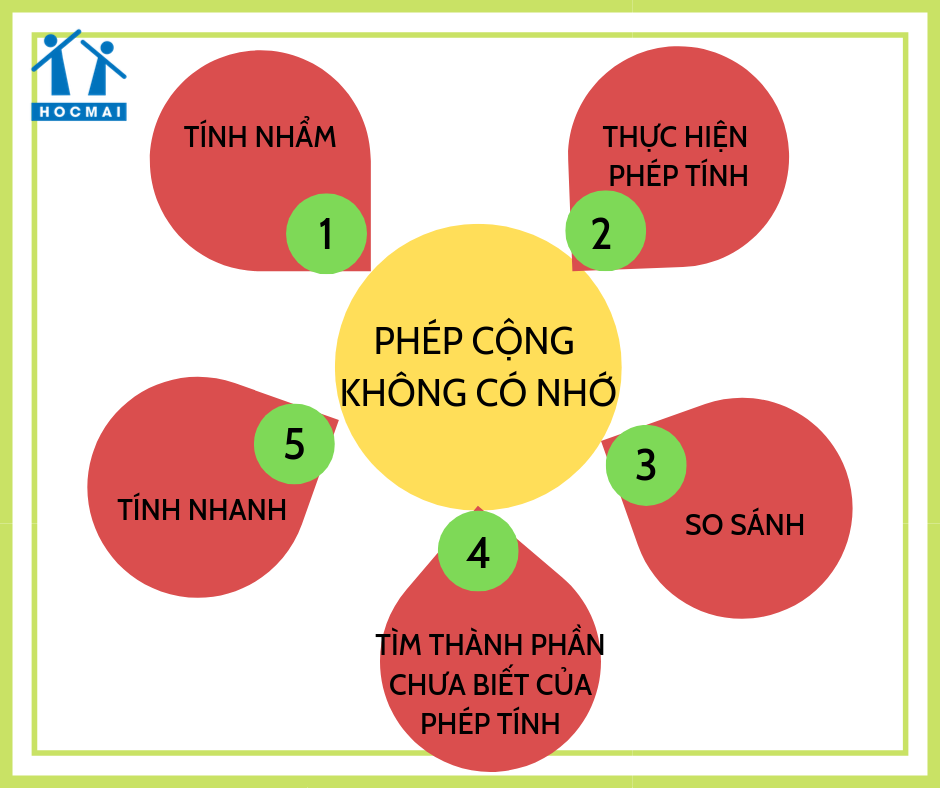
(Các dạng bài liên quan tới phép cộng không có nhớ)
Dạng 2: Thực hiện phép tính.
Bài 1: Đặt tính rồi tính.
Quy tắc:
– Các chữ số trong cùng 1 hàng sẽ thẳng cột với nhau (Hàng trăm thẳng hàng trăm, hàng chục thẳng hàng chục, hàng đơn vị thẳng hàng đơn vị)
– Bắt đầu thực hiện phép cộng từ các số thuộc hàng bé nhất: đơn vị, tới hàng chục, hàng trăm, hàng nghìn,…
– Viết số có nhiều chữ số hơn trước, số có ít chữ số ở sau (Phép cộng số có 3 chữ số và 2 chữ số thì sẽ đặt số có 3 chữ số trước, số có 2 chữ số sau)
Ví dụ: 456 + 120
456 Ta có: 6 cộng 0 bằng 6
+120 5 cộng 2 bằng 7
= 576 4 cộng 1 bằng 5
Kết quả là: 576
Bài 2: Khoanh tròn vào chữ cái trước câu trả lời đúng nhất.
Quy tắc:
– Một dãy các phép tính cộng sẽ thực hiện phép tính tuần tự từ trái sang phải.
– Thực hiện phép tính cộng giữa 2 số hạng hoặc cả 3 số hạng cùng một lúc.
– Khoanh tròn đáp án.
Ví dụ: 241 + 124 + 201 = ?
A. 665 B. 566 C. 656 D. 666
Nhận xét: Đây là một phép tính có 3 số hạng, và mỗi số hạng đều là số có 3 chữ số. Do đó, có thể tách phép tính này thành 2 phép tính.
Phép tính 1: 241 + 124 = 365
Phép tính 2: 365 (Kết quả của phép tính 1) + 201 = 566
Vậy đáp án là B. 566
Dạng 3: So sánh
Bài 1: Điền dấu (<; =; >) thích hợp vào chỗ trống.
Quy tắc:
Cách 1: Tính tổng
– Tính tổng của 1 vế.
– Đem kết quả so sánh với vế còn lại (So sánh từ hàng lớn nhất tới hàng bé nhất. Hàng nghìn, hàng trăm, hàng chục, hàng đơn vị)
– Điền dấu thích hợp.
Cách 2: Tách số
– Tách vế có một số thành một tổng, sao cho trong đó có 1 số hàng bằng với 1 số hạng của vế khác.
– So sánh các số hạng còn lại với nhau.
– Điền dấu thích hợp.
Ví dụ: 42 + 100 … 124
Cách 1: Ta thực hiện phép tính: 42 + 100 = 142.
So sánh 124 và 124 thì 142 lớn hơn 124.
Nên 42 + 100 > 124
Cách 2: Ta thực hiện tách số 124 = 24 + 100 (Trong đó, số hạng thứ hai của vế phải là 100 bằng với số hạng thứ hai của vế trái)
So sánh hai số hạng còn lại là 24 và 42 thì 42 > 24
Nên 42 + 100 > 24 + 100
Suy ra: 42 + 100 > 124
Dạng 4: Tìm thành phần chưa biết của phép tính.
Bài 1: Tìm X
Quy tắc:
– Xác định vai trò của X (Số bị trừ)
– Nếu vế phải là một số thì thực hiện phép tính như bình thường. Nếu vế phải là một tổng thì tính tổng trước rồi mới thực hiện tìm X
Ví dụ:
X – 15 = 214
X = 214 + 15
X = 229
X – 15 = 200 + 30
X – 15 = 230
X = 230 + 15
X = 245
Bài 2: Điền chữ số còn thiếu vào dấu *
Quy tắc:
– Dựa vào nguyên tắc đặt tính rồi tính, ta thực hiện lần lượt từ phải qua trái, từ hàng bé nhất tới hàng lớn nhất.
– Nếu dấu * nằm ở Tổng, ta thực hiện cộng như bình thường. Nhưng nếu dấu * nằm ở một chữ số nào đó nằm ở số hạng, thì ta thực hiện lấy chữ số hàng đó ở tổng trừ đi chữ số hàng đó ở số hạng còn lại.
Ví dụ:
* 5
+ 42
= 7*
Dấu * nằm ở hàng chục của số hạng đầu tiên và hàng đơn vị của tổng.
Ta có, dấu sao ở hàng đơn vị của tổng = 5 + 2 = 7
Dấu sao nằm ở hàng chục của số hạng đầu tiên = hàng chục của tổng – hàng chục của số hạng thứ hai = 7 – 4 = 3
Vậy, phép tính đầy đủ là:
35
+ 42
= 77
Dạng 5: Tính nhanh
Bài 1: Tính bằng cách thuận tiện
Quy tắc:
– Đưa về các con số tròn chục hay tròn trăm.
– Nhóm các số hạng với nhau, sử dụng các tính chất của phép cộng (giao hoán, kết hợp).
Ví dụ: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
Ta thấy 1 + 9 = 10
2 + 8 = 10
Tương tự với các số hạng còn lại thì ta được một dãy số như sau:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
= 1 + 9 + 2 + 8 + 3 + 7 + 4 + 6 + 5
= 10 + 10 + 10 + 10 + 5
= 45
Vậy là cô Nguyễn Thị Huệ (Hocmai Tiểu học) đã hướng dẫn cho tất cả các em học sinh về những dạng bài liên quan tới phần phép cộng không có nhớ. Đây đều là các dạng bài cơ bản nhất mà các em có thể dễ dàng bắt gặp trong chương trình học hay những bài kiểm tra. Để học tốt hơn phần đơn vị kiến thức này, hãy theo dõi phần tiếp theo về phép cộng có nhớ nhé!
Phụ huynh và học sinh có thể tham khảo thêm bài giảng miễn phí trong CHƯƠNG TRÌNH HỌC TỐT 2020-2021 của HOCMAI để củng cố thêm kiến thức môn Toán lớp 3. Thông qua chương trình, học sinh không những nắm vững được kiến thức cơ bản trong sách giáo khoa mà còn rèn luyện được tính tự giác và chủ động hơn trong học tập mà không cần bố mẹ phải nhắc nhở.
Chúc các em học tốt cùng Hocmai Tiểu học và giành được những điểm số cao trên trường!
>>> Phụ huynh ĐĂNG KÝ NHẬN BÀI GIẢNG miễn phí cho con ngay tại đây: https://hocmai.link/hoctothocthumonToan
Đăng ký Chương trình Học Tốt 2020 – 2021
Thông tin chi tiết về khóa học, phụ huynh và học sinh hãy gọi ngay hotline 0936 5858 12 để được tư vấn miễn phí. |






















