Thi vào 10 môn Toán: Bí quyết để ghi trọn điểm dạng bài chứng minh tứ giác nội tiếp

Chứng minh hình học là một trong những dạng bài khó đạt được điểm tuyệt đối mà học sinh sẽ gặp nhiều trong đề thi học kỳ lớp 9, đặc biệt là đề thi vào lớp 10.

Đặc biệt với dạng bài chứng minh tứ giác nội tiếp, học sinh gặp nhiều khó khăn khi phải liên hệ, vận dụng nhiều kiến thức hình đã được học. Nhằm xóa tan nỗi lo lắng của học sinh với dạng này, thầy Hồng Trí Quang – giáo viên bộ môn Toán tại Hệ thống Giáo dục HOCMAI sẽ hướng dẫn những mẹo hay, ghi trọn điểm dạng bài tập này với phương pháp dễ nhớ và áp dụng, cụ thể như sau:

Thầy Hồng Trí Quang hướng dẫn học sinh về nội dung “Tứ giác nội tiếp”

Kiến thức về đường tròn học sinh cần ghi nhớ

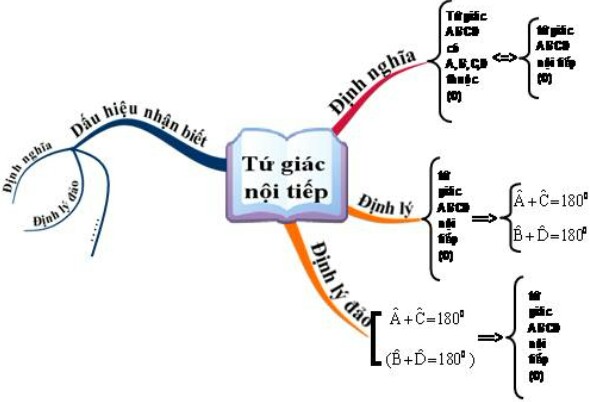
Định nghĩa: Một tứ giác có bốn đỉnh cùng nằm trên một đường tròn gọi là tứ giác nội tiếp đường tròn.

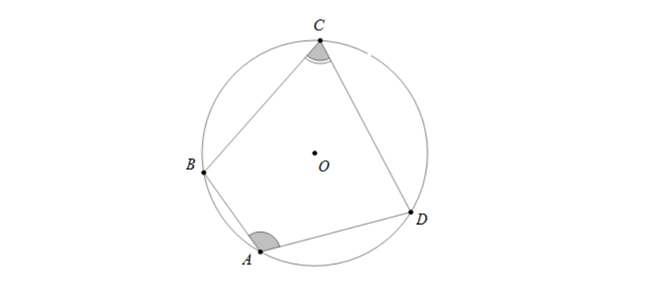
Hình minh họa: Tứ giác ABCD nội tiếp đường tròn tâm O

Định lý: Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180 độ.

Ví dụ, cho tứ giác ABCD nội tiếp đường tròn tâm O, ta suy ra được:

Định lý đảo: Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180 độ thì tứ giác đó nội tiếp được đường tròn.

Nhắc lại một số kiến thức đã học

+ Hai góc nội tiếp cùng chắn một cung thì bằng nhau.

+ Góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung.

+ Góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp cùng chắn một cung.

Một số phương pháp chứng minh Tứ giác nội tiếp

Trong bài giảng của mình thầy Hồng Trí Quang đã đưa ra những phương chứng minh tứ giác nội tiếp ngắn gọn, dễ hiểu để học sinh nắm được, từ đó có thể vận dụng vào việc làm bài tập. Cụ thể như sau:

Phương pháp 1: Chứng minh cho bốn đỉnh của một tứ giác cách đều một điểm nào đó.

Nếu đề bài cho trước một đường tròn tâm O có bán kính R thì bất kỳ điểm nào nằm trên đường tròn đều cách tâm một khoảng đúng bằng bán kính. Theo thầy Quang hướng dẫn, dựa vào tính chất này, học sinh có thể dễ dàng chứng minh một tứ giác nội tiếp một đường tròn.

Ví dụ: Cho một điểm O cố định và tứ giác ABCD.

Nếu học sinh chứng minh được bốn điểm A, B, C, D cách đều điểm O với khoảng cách bằng R, tức OA = OB = OC = OD = R  thì điểm O chính là tâm đường tròn đi qua bốn điểm A, B, C, D. Hay nói cách khác, tứ giác ABCD nội tiếp đường tròn tâm O bán kính R.

Phương pháp 2: Chứng minh tứ giác có hai góc đối bằng 180 độ.

Nếu đề bài cho trước tứ giác ABCD và học sinh tính được tổng số đo hai góc đối diện bằng 180 độ thì chứng minh được tứ giác ABCD nội tiếp một đường tròn nào đó.

Thầy Quang hướng dẫn học sinh phương pháp chứng minh tổng hai góc đối bằng 180 độ

Phương pháp 3: Chứng minh tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.

Ở phương pháp này, học sinh chú ý phải nhìn đúng hình đúng góc, nếu không sẽ có cách chứng minh sai nhưng kết quả đúng và ảnh hưởng tới những câu tiếp theo. Cụ thể, khi đề bài cho tứ giác ABCD và chứng minh được góc ngoài tại đỉnh A bằng góc C của tứ giác (góc A và góc C đối đỉnh) thì có thể kết luận tứ giác ABCD là tứ giác nội tiếp.

Thầy Quang hướng dẫn học sinh áp dụng phương pháp 3 vào bài toán thực tế

Phương pháp 4: Chứng minh hai đỉnh cùng kề một cạnh, cùng nhìn cạnh đó dưới hai góc bằng nhau và bằng 90 độ.

Phương pháp này áp dụng khi đề bài cho tứ giác ABCD và những dữ kiện gợi ý tính được rằng số đo góc DAC bằng số đo góc DBC bằng 90. Từ đó, học sinh có thể kết luận tứ giác ABCD nội tiếp đường tròn.

Những điều học sinh cần lưu ý

Đối với dạng bài chứng minh tứ giác nội tiếp, thầy Hồng Trí Quang lưu ý học sinh cần đọc kỹ đề và vẽ hình chính xác, tránh vào những trường hợp đặc biệt. Ngoài ra, học sinh cũng cần nắm rõ những kiến thức hình học cơ bản để có thể áp dụng linh hoạt vào bài tập.

Trên đây là một số lưu ý giúp học sinh học thật tốt dạng bài tập tứ giác nội tiếp. Học sinh có thể học và luyện giải các dạng bài tương tự để nắm chắc kiến thức phần tứ giác nội tiếp. Trong thời điểm này, học sinh lớp 9 hãy tham khảo Giải pháp HM10 toàn diện để trang bị sớm kiến thức học kì II và ôn tập, luyện đề thi vào lớp 10.

Đây là chương trình dành riêng cho học sinh lớp 9 sắp thi vào lớp 10 với lộ trình học tập toàn diện, khoa học từ việc trang bị, hệ thống toàn bộ kiến thức nền tảng, cơ bản, tổng ôn các kiến thức theo từng chuyên đề/ dạng bài và rèn luyện kĩ năng, tích lũy kiến thức làm bài thông qua việc luyện đề. Từ đó, giúp học sinh gia tăng cơ hội đạt điểm cao trong năm học lớp 9 và thi vào 10 đạt điểm cao. Phụ huynh, học sinh tham khảo chương trình Toán lớp 9 và thi vào 10 tại https://hocmai.link/Chinh-Phuc-Ki-Thi-Vao-10