Trong bài giảng hôm nay, thầy Lưu Huy Thưởng sẽ cùng các bạn học sinh tìm hiểu về “Một số hệ thức về cạnh và đường cao trong tam giác vuông”. Đây là kiến thức cơ sở để học tốt các dạng toán hình học khác trong chương trình lớp 9. Bên cạnh những lý thuyết quan trọng, thầy Thưởng sẽ chia sẻ cách giải các dạng bài tập liên quan. Cùng theo dõi nhé!
>>> Xem đầy đủ bộ bài giảng môn Toán lớp 9 của thầy Thưởng tại: https://hocmai.link/bai-giang-toan-9-thay-thuong-1310
Tổng hợp lý thuyết quan trọng cần ghi nhớ
Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền

Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP
Định lí 1: Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông trên cạnh huyền.
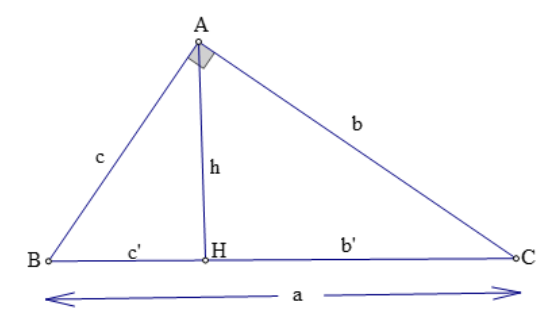
Trong tam giác ABC vuông tại A có: b²= a.b’; c²= a.c’
Chứng minh định lí: ΔCAH ∼ ΔCAB(g.g) ⇒ AC/CB= CH/CA ⇔ b/a= b’/b ⇔ b²= a.b’
Để hiểu hơn về định lí 1, các bạn học sinh có thể theo dõi chi tiết những ví dụ của thầy Thưởng trong video bài giảng
Một số hệ thức liên quan đến đường cao
Định lí 2: Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
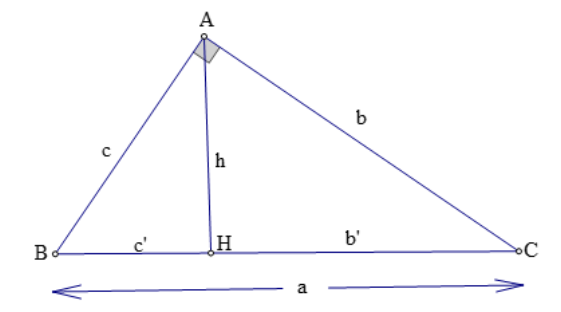
Trong tam giác ABC vuông tại A có: h²= b’.c’
Chứng minh định lí: ΔCHA ∼ ΔAHB(g.g) ⇒ HA/HB= CH/AH ⇔ h/c’= b’/h ⇔ h²= b’.c’
Để hiểu hơn về định lí 2, các bạn học sinh có thể theo dõi chi tiết những ví dụ của thầy Thưởng trong video bài giảng
Định lí 3: Trong tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
Trong tam giác ABC vuông tại A có: b.c = a.h
Chứng minh định lí: ΔCHA ∼ ΔCAB(g.g) ⇒ CA/CB= HA/AB ⇔ b/a= h/c ⇔ b.c = a.h
Định lí 4: Trong tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
Trong tam giác ABC vuông tại A có: 1/h²= 1/b²+ 1/c²
Chứng minh định lí: Xét tam giác ABC vuông tại A, đường cao AH, a²= b²+ c²(định lý Py-ta-go). Bình phương 2 vế của công thức b.c = a.h, ta có:
b².c²= a².h²
1/b².c²= 1/a².h²
a²/b².c²= 1h²
b²+ c²/b².c²= 1/h²
1/c²+ 1/b²=1/h²
Để hiểu hơn về định lí 3 và 4, các bạn học sinh có thể theo dõi chi tiết những ví dụ của thầy Thưởng trong video bài giảng
Các dạng bài thường gặp về hệ thức cạnh và đường cao trong tam giác vuông
Dạng 1: Tính độ dài các đoạn thẳng trong tam giác vuông
Phương pháp: Sử dụng hệ thức về cạnh và đường cao trong tam giác vuông.
Dạng 2: Chứng minh các hệ thức liên quan giữa các yếu tố trong tam giác vuông
Phương pháp:
Ta thường sử dụng các kiến thức:
- Đưa về hai tam giác đồng dạng có chứa các đoạn thẳng có trong hệ thức.
- Sử dụng các hệ thức về cạnh và đường cao trong tam giác vuông để chứng minh.
Để nắm chắc kiến thức về hệ thức cạnh và đường cao trong tam giác vuông, các bạn học sinh nhớ xem lại video bài giảng của thầy Thưởng, thực hành các ví dụ và tìm thêm những bài tập liên quan để củng cố kiến thức đã được học.
Bên cạnh đó, để học tốt môn Toán 9 cũng như chuẩn bị kiến thức tốt nhất cho kỳ thi vào 10, các bạn học sinh cần có lộ trình học tập hợp lí để vừa có thời gian trang bị kiến thức vừa đẩy sớm quá trình luyện đề. Các bạn có thể tham khảo Chương trình HM10 Toàn diện của HOCMAI để bổ sung thêm một phương pháp học tập tốt nhất. Với lộ trình học 3 bước gồm Trang bị kiến thức – Tổng ôn – Luyện đề đảm bảo mang lại cho học sinh những trải nghiệm thú vị từ những bài giảng chất lượng của các thầy cô giàu kinh nghiệm luyện thi vào 10.
ĐĂNG KÝ TẠI ĐÂY ĐỂ NHẬN BÀI GIẢNG HỌC THỬ MIỄN PHÍ MÔN TOÁN 9
ĐĂNG KÝ GIẢI PHÁP HM10 TOÀN DIỆN 2021 – 2022
Mọi thông tin chi tiết về khóa học vui lòng liên hệ hotline 0936585812 để được |


















