Hàm số bậc nhất là phần kiến thức tưởng chừng như đơn giản trong chương trình toán lớp 9, tuy nhiên đây cũng là phần khiến rất nhiều em học sinh bị mất điểm do chủ quan trong qua quá trình giải bài tập. Chính vì vậy, HOCMAI sẽ tổng hợp và chia sẻ kiến thức và các dạng bài thường gặp về hàm số bậc nhất để các em học sinh có thể nắm được.
A. Lý thuyết về hàm số bậc nhất
1. Định nghĩa
Hàm số bậc nhất là hàm số được cho bởi công thức
y = ax + b
Trong đó:
a, b là số thực với a ≠ 0
Lưu ý:
Trong trường hợp b = 0, hàm bậc nhất có dạng
y = ax
- Đây là hàm số có đồ thị biểu diễn trên trục Oxy đi qua trục tọa độ
- Hàm số y = ax biểu thị tương quan tỉ lệ giữa 2 biến x và y
2. Tính chất của hàm số bậc nhất
- Hàm số bậc nhất xác định với mọi giá trị của x thuộc R
- Hàm số bậc nhất có tính đồng biến và nghịch biến dựa vào a:
+ Trong trường hợp a > 0 ⇒ Hàm số đồng biến trên tập R
+ Trong trường hợp a < 0 ⇒ Hàm số nghịch biến trên tập R
B. Sự biến thiên của hàm số bậc nhất
1. Sự đồng biến và nghịch biến của hàm số bậc nhất
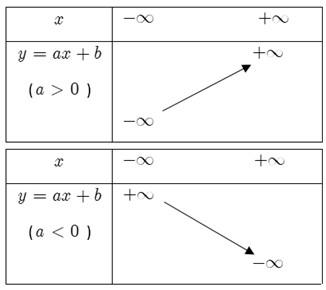
Dựa trên tính chất của hàm bậc nhất, ta có thể thấy được hàm số y = ax + b (a≠0) là hàm số có tập xác định D = R, đồng biến trên R nếu a > 0 và nghịch biến trên R nếu a < 0.
Bảng biến thiên của hàm số bậc nhất được thể hiện như sau:
B. Một số dạng bài thường gặp về hàm số bậc nhất
Các dạng bài về hàm số bậc nhất
Dạng bài tập 1: Xác định hàm số bậc nhất
Để làm được dạng bài này, các em học sinh cần nhớ về định nghĩa và các tính chất của hàm số bậc nhất có dạng y = ax + b (điều kiện a≠0).
Bài tập minh họa: Tìm điều kiện của m để các hàm số dưới đây là hàm số bậc nhất:
a) y = (m-2)x + m
b) y = (m²-2x-3)x2 + (m+1)x + m
c) y = √(m²-1).x + 2 .
Hướng dẫn giải:
a) Để hàm số y = (m-1)x + m là hàm số bậc nhất
⇔ m – 1 ≠ 0 ⇔ m ≠ 1.
Kết luận: Với mọi của m ≠ 1 thì hàm số y = (m – 1)x + m là hàm số bậc nhất.
b) Ta có:
(m² -2x – 3) x 2 + (m+1)x + m
= 2m² – 4x – 6 + (m+1)x + m
= (m-3)x + 2m² + m – 6
Để hàm số y = (m² – 2x -3) x 2 + (m+1)x + m là hàm số bậc nhất
⇔ m + 1 ≠ 0 ⇔ m ≠ -1
Vậy khi m ≠ -1 thì hàm số y = (m² – 2x -3) x 2 + (m+1)x + m là hàm số bậc nhất
c) Để hàm số y = √(m² – 1)x + 2 là hàm bậc nhất
⇔ √(m² – 1) ≠ 0 ⇔ m² – 1 > 0 ⇔ m > 1 hoặc m < -1.
Vậy với m > 1 hoặc m < -1 thì hàm số y = √(m² – 1)x + 2 là hàm bậc nhất.
Dạng 2: Tìm m để hàm số đồng biến, nghịch biến
Dựa trên tính chất của hàm bậc ta có hàm số bậc nhất y = ax + b, (a≠0) đồng biến và nghịch biến khi:
-
Trường hợp a < 0 hàm số là hàm đồng biến với mọi x thuộc R
-
Trường hợp a < 0 hàm số là hàm nghịch biến với mọi x thuộc R
Bài tập mình họa: Xác định a để các hàm số dưới đây thỏa mãn điều kiện sau:
a) y = (a + 2)x + 3 đồng biến trên R.
b) y = (m² – m).x + m nghịch biến trên R.
Hướng dẫn giải:
a) Để hàm số y = (a + 2)x + 3 đồng biến với mọi x thuộc R
⇔ a + 2 > 0 ⇔ a > -2.
Vậy khi a > -2 thì hàm số hàm số y = (a + 2)x + 3 đồng biến với mọi x thuộc R
b) Để hàm số y = (m² – m).x + m nghịch biến với mọi x thuộc R.
⇔ m² – m < 0 ⇔ m (m – 1) < 0 ⇔ 0 < m < 1.
Vậy khi 0 < m < 1 thì hàm y = (m² – m).x + m nghịch biến với mọi x thuộc R.
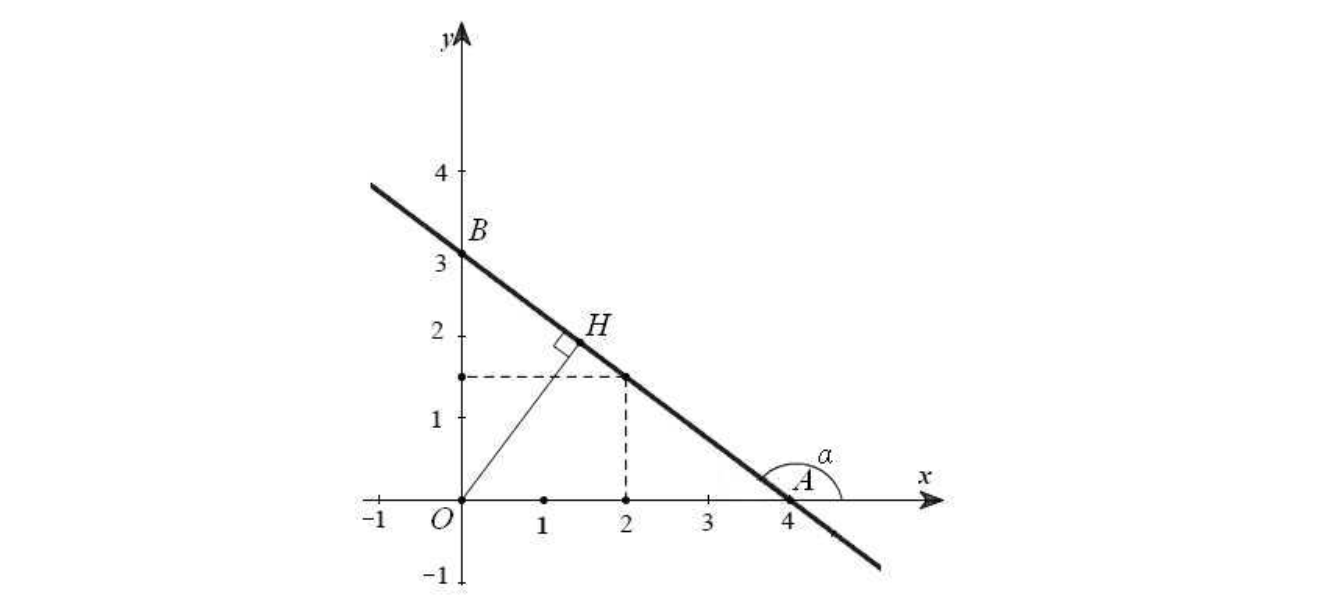
Dạng 3: Tìm hàm số đi qua 2 điểm bất kỳ
Các bước giải dạng bài tập này như sau:
Bước 1: Gọi hàm số có dạng y = ax + b (với a ≠ 0)
Bước 2: Thay thế tọa độ của 2 điểm đã cho vào đồ thị trên vào x và y
Bước 3: Giải hệ phương trình 2 ẩn a và b
Bước 4: Kết luận hàm số bậc nhất đi qua 2 điểm đã cho
Các dạng bài xét biến thiên của hàm số
Dạng bài 1: Tìm điều kiện để hàm số đồng biến hoặc nghịch biến
a, y= 5x – (2-x)k đồng biến, nghịch biến.
b, y= (k² – 4)x – 2 đồng biến.
c, y= (-k² + k – 1)x – 7 nghịch biến.
d, y= (4 – 4k + k²)x + 2 đồng biến.
Hướng dẫn giải:
a, Ta có y= 5x – (2-x)k = 5x – 2k + k.x = (5+k)x – 2k
Từ phương trình trên ta có có hệ số của hàm số là a = 5+k. Khi đó:
-
Để hàm số là hàm đồng biến ⇔ a > 0 ⇔ 5 + k > 0 ⇔ k > -5
-
Để hàm số là hàm nghịch biến ⇔ a < 0 ⇔ 5 + k < 0 ⇔ k < -5.
C. Một số bài tập tự luyện về hàm số bậc nhất
Trên đây là các kiến thức cơ bản và các dạng bài thường gặp về hàm số bậc nhất trong chương trình toán lớp 9. Hy vọng bài viết trên sẽ cung cấp các kiến thức bổ ích dành cho các em học sinh trong quá trình giải bài tập, ôn thi học kỳ hay ôn thi vào 10 môn Toán.
Tham khảo thêm: Nhắc lại và bổ sung các khái niệm về hàm số
