Hàm số là phần kiến thức quan trọng không chỉ trong chương trình toán lớp 9 mà còn xuyên suốt trong chương trình toán đại số của THPT. Chính vì vậy đây là phần kiến thức quan trọng mà các em học sinh cần phải nắm vững.
A. Nhắc lại lý thuyết về hàm số
1. Nhắc lại định nghĩa về hàm số
+ Nếu một đại lượng y nào đó phụ thuộc vào sự thay đổi của một đại lượng x, ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
Ký hiệu: y = f(x)
+ Hàm số trên được thể hiện theo 2 dạng: Bằng bảng hoặc bằng đồ thị hàm số
Ví dụ:
- Khi y là hàm số của x được thể hiện theo dạng bảng được thể hiện như sau:
| x | 2 | 1/2 | 3 | 1 |
| y | 4 | 8 | 1/6 | 1 |
- Khi y là hàm số của x được cho thể hiện dưới dạng công thức được thể hiện như sau:
y = 2x + 1; y = x + 9; y = 5x
+ Hàm số thường được biểu thị dưới dàng chữ cái như f, g, h, … ví dụ khi y là hàm số của biến số x, ta có thể viết ký hiệu như sau: y = f(x); y = g(x) hoặc y = h(x)
+ f(a) được gọi là giá trị của hàm số y = f(x) khi x = a. Khi hàm số y được biểu thị dưới dạng bởi công thức y = f(x), muốn tính giá trị f(a) của hàm số tại x = a, ta thay x = a vào biểu thức f(x) rồi thực hiện các phép tính dựa trên biểu thức của f(x) để tính ra giá trị
Ví dụ:
Ta có hàm số y = f(x) = x + 9. Khi đó:
- f(1) = 1 + 9 = 10
- f(3) = 3 + 9 = 12
+ Trường hợp đặc biệt: Nếu hàm số y = f(x) mà khi x thay đổi mà y luôn nhận một giá trị cố định thì hàm số dã cho y là một hàm hằng.
Ví dụ:
Ta có y = f(x) = 19√3. Lúc này, với mọi giá trịnh của x thì y luôn bằng 19√3 vậy hàm số đã cho là một hàm hằng.
2. Đồ thị của hàm số
Khi ta biểu diễn tất cả các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ Oxy , ta sẽ được đồ thị của hàm số y = f(x).
Ví dụ:
Khi biểu diễn tất cả các cặp giá trị tưng ứng của hàm số f(x) = x + 4 lên mặc phẳng tọa độ Oxy, ta sẽ được đồ thị như sau:
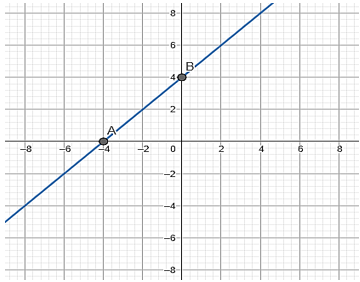
Các cặp giá trị tương ứng trên mặt phẳng tọa độ là A(-4; 0); B(0; 4).
3. Khái niệm về hàm đồng biến và hàm nghịch biến
Cho một hàm số có dạng y = f(x) xác định với mọi giá trị của x ∈ R
+ Trong trường hợp giá trị của biến x tăng lên mà giá trị của f(x) cũng tương ứng tăng lên thì ta có hàm số y = f(x) là hàm đồng biến trên tập xác định R (Có thể gọi là hàm số đồng biến).
+ Và ngược lại, trong trường hợp giá trị của biến x tăng nhưng giá trị của biểu thức f(x) tương ứng lại giảm thì ta kết luận hàm số y = f(x) được gọi là hàm số nghịch biến trên R (Có thể gọi là hàm số nghịch biến).
Kết luận lại, khi có một hàm số có dạng y = f(x) xác định trên tập số thực R. Với các giá trị x1, x2 ∈ R ta có:
+ Trong trường hợp x1 < x2 mà f(x1) < f(x2) thì kết luận hàm số đồng biến.
+ Trong trường hợp x1 < x2 mà f(x1) > f(x2) thì kết luận hàm số nghịch biến.
Ví dụ:
Cho hàm số y = x + 6, xác định với ∀ x ∈ R
Với các giá trị x1 và x2 ta có x1 < x2 ⇒ x1 + 6 < x2 + 6
Suy ra f(x1) < f(x2) nên hàm số y = x + 6 đồng biến trên R.
B. Các dạng bài tập thường gặp
Dạng 1 : Tính giá trị của hàm số đã cho tại 1 điểm bất kỳ
Phương pháp làm bài: Để tính giá trị của hàm số y = f(x) tại 1 điểm x1 bất kỳ, ta thay giá trị x1 vào hàm số f(x) từ đó ta sẽ tính được y1 = f(x1)
Dạng 2 : Biểu diễn tọa độ của một điểm và xác định điểm thuộc đồ thị hàm số
Phương pháp làm bài: Trên trục Oxy, để điểm M nằm trên đồ thị y = f(x) thì điểm M phải thỏa mãn điều kiện có tọa độ x1 và y1 sao cho y1 = f(x1)
Dạng 3 : Xét sự đồng biến và nghịch biến của hàm số
Phương pháp làm bài:
Bước 1: Tìm tập xác định của hàm số là D
Bước 2: Giả sử có 2 giá trị x1 và x2 thuộc tập xác định D sao cho x1 < x2
Bước 3: Thay 2 giá trị x1 và x2 vào hàm f(x) rồi tiến hành so sánh.
- Nếu f(x1) < f(x2) ta kết luận hàm số đồng biến
- Nếu f(x1) > f(x2) ta kết luận hàm số nghịch biến
Dạng 4 : Bài toán liên quan đến đồ thị hàm số y = ax (a≠0)
Phương pháp làm bài: Hàm số có dạng y = ax (a ≠ 0)
Khi biểu diễn trên trục tọa độ Oxy, đây là hàm số đi qua gốc tọa độ O và điểm M (1,a)
Cho 2 điểm bất kỳ A (xa,ya) và B(xb,yb). Khi đó, độ dài của đoạn AB sẽ được tính theo công thức:
AB = √[(xb – xa)² + (yb – ya)²]
Một số bài tập vận dụng:
Bài tập 1: Xác định hàm số f(x) biết rằng f(x + 1) = x2 – 2x + 3
Giải:
Điều kiện: x ∈ R
Ta đặt x + 1 = t vậy x = t – 1
Lúc này f(t) = (t – 1)2 – 2(t – 1) + 3 = t2 – 4t + 6
Vậy kết luận hàm số f(x) = x2 – 4x + 6 với mọi x ∈ R
Bài tập 2: Chứng minh công thức tính khoảng cách của hai điểm A(x1; y1) và B(x2; y2) là
AB = √[(x2 – x1)² + (y2 – y1)²]
Giải:
Gọi điểm C là điểm thỏa mãn điều kiện C (x2; y1)
+ Vậy khoảng cách giữa x1, x2 trên trục hoành được tính là AC = |x2 – x1|
+ Vậy khoảng cách giữa y1, y2 trên trục tung được tính là BC = |y2 – y1|
Mà tam giác ABC là tam giác vuông tại C. Nên theo định lý Pitago ta có: AB2 = AC2 + BC2 = (x2 – x1)2 + (y2 – y1)2
Vậy khi đó khoảng cách AB = √[(x2 – x1)² + (y2 – y1)²]
Tham khảo thêm:
















