Tiếp nối chương trình “Học online cùng HOCMAI, thầy Phạm Ngọc Hưng – Giáo viên môn Toán tại Hệ thống Giáo dục HOCMAI chỉ ra cho học sinh các phần kiến thức trọng tâm trong bài học “Chứng minh tiếp tuyến của đường tròn nhờ góc tạo bởi tiếp tuyến và dây cung” dưới đây.
Phụ huynh, học sinh xem chi tiết bài giảng trong video dưới đây:
Hệ thống kiến thức cần nhớ
Theo thầy Hưng, nội dung kiến thức trong bài học này không chỉ có liên quan đến các bài kiểm tra, bài thi trong học kỳ II của học sinh lớp 9 mà nó còn là phần kiến thức quan trọng, thường xuyên xuất hiện trong đề thi môn Toán vào lớp 10. Do đó, học sinh cần nắm vững các kiến thức này để không bị mất điểm đáng tiếc trong những bài kiểm tra, bài thi quan trọng.

Thầy Phạm Ngọc Hưng – Giáo viên môn Toán tại Hệ thống Giáo dục HOCMAI.
Định nghĩa: Cho đường tròn (O) có Ax là tia tiếp tuyến tại tiếp điểm A và dây cung AB. Khi đó, góc BAx là góc tạo bởi tia tiếp tuyến và dây cung.
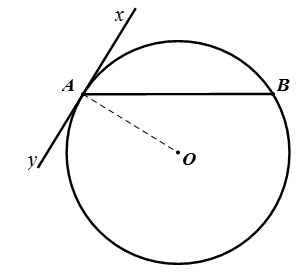
Ví dụ: Hãy chứng minh đường thẳng d là tiếp tuyến của (O, R) cho trước.
Ví dụ về bài toán chứng minh tia tiếp tuyến của đường tròn cho trước.
Phương pháp 1: Ta chứng minh khoảng cách từ O đến đường thẳng d bằng R.
Cụ thể: Hạ OH vuông góc với d, ta chứng minh rằng: OH=R.
Phương pháp 2: Giả sử d cắt (O) tại A. Ta chứng minh rằng: (d) vuông góc OA.
Phương pháp 3: Áp dụng các định lý và hệ quả để giải bài toán.
Định lý: Góc tạo bởi tiếp tuyến và dây cung là góc bằng ½ số đo của cung đó.
Hệ quả:
- Góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chứa dây cung đó.
- Cho tam giác ABC, tia Ax và AB nằm cùng phía so với đường thẳng AC sao cho góc xAB bằng góc ACB thì Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
Bài tập tự luyện
Bài 1: Cho ΔABC nội tiếp đường tròn (O), (AB < AC). Trên tia đối của tia BC lấy điểm M sao cho MA2 = MB.MC. Chứng minh rằng: MA là tiếp tuyến của đường tròn (O).
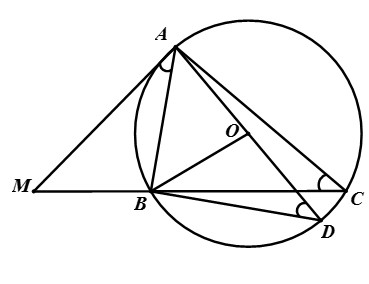
Vì MA2 = MB.MC => MA/MB = MC/MA
Xét ΔMAC và ΔMBA có:
∠M chung
MA/MB = MC/MA
=> ΔMAC ∼ ΔMBA (c.g.c)
=> ∠MAB = ∠MCA (1)
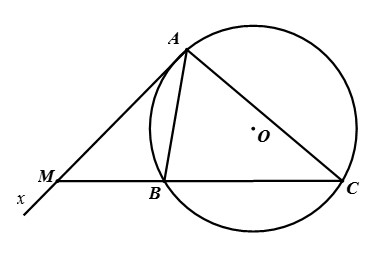
Kẻ đường kính AD của (O)
Ta có ∠ACB = ∠ADB (hai góc nội tiếp cùng chắn cung AB )
Mà ∠MAB = ∠MCA (chứng minh trên)
Suy ra ∠MAB = ∠ADB (3)
Lại có ∠ABD = 90o (góc nội tiếp chắn nửa đường tròn)
=> ∠BAD + ∠BDA = 90o (4)
Từ (3) và (4) suy ra ∠BAD + ∠MAB = 90o hay ∠MAO = 90o
=> OA ⊥ MA
Do A ∈ (O)
=> MA là tiếp tuyến của (O).
Trên đây là hệ thống kiến thức trọng tâm và bài tập tự luyện nhằm giúp các bạn học sinh ghi nhớ nội dung bài giảng “Chứng minh tiếp tuyến của đường tròn nhờ góc tạo bởi tiếp tuyến và dây cung”. Để học thêm bài giảng các môn Toán, Ngữ văn, tiếng Anh từ lớp 6-9 trong học kỳ II, phụ huynh học sinh hãy chú ý đón xem chương trình “Học online cùng HOCMAI” và “Lớp học không khoảng cách”.
Chương trình Lớp học không khoảng cách được phát sóng trực tiếp trên các kênh VTC8, VTC11 và VTC Now do Đài truyền hình kỹ thuật số VTC phối hợp với Hệ thống Giáo dục HOCMAI thực hiện.
Chương trình Học online cùng HOCMAI được phát sóng trực tiếp trên Fanpage Hocmai.vn THCS và kênh Youtube HOCMAI THCS.
Chương trình sẽ giúp học sinh nắm chắc một phần các kiến thức quan trọng trong học kỳ II, từ đó giúp học sinh tự học trực tuyến tại nhà hiệu quả và bứt phá điểm số trong các bài kiểm tra, bài thi trong thời gian tới.
Song song với đó, phụ huynh học sinh có thể tham khảo Chương trình Học tốt học kỳ II của HOCMAI để được học tập theo lộ trình học kỳ II bài bản với nội dung kiến thức bám sát sách giáo khoa cùng hệ thống bài tập, đề kiểm tra, đề thi thường xuyên để đánh giá năng lực học tập của học sinh, giúp học sinh tự tin chinh phục điểm 9, 10.
ĐĂNG KÝ NGAY: http://bit.ly/BÍ-KÍP-HỌC-TỐT
Mọi thông tin thắc mắc về chương trình vui lòng liên hệ hotline 0936585812 để được giải đáp miễn phí!























