Bài học “Tập hợp, phần tử của tập hợp” nằm trong chương “Số tự nhiên” của bộ môn Toán 6, sách Chân trời sáng tạo. Ở chương này, học sinh sẽ được thầy cô hướng dẫn tìm hiểu những kiến thức về tập hợp, tập hợp các số tự nhiên, các phép tính trên tập hợp số tự nhiên,… Qua đó, các em sẽ có cơ hội được ứng dụng kiến thức từ bài học vào trong cuộc sống, từ đó phát triển năng lực bản thân. Bước vào năm học mới rồi, học sinh lớp 6 cùng theo dõi, tham khảo bài viết dưới đây để học tốt môn Toán nhé các em.
Video bài giảng của cô Khánh Vy:
I/ Mục tiêu bài học:
Trước mỗi bài học, cô Vy luôn khuyến khích các bạn học sinh hãy cùng nhau đề ra mục tiêu cần đạt được sau khi kết thúc buổi học và phấn đấu thực hiện để tiến bộ. Cụ thể, mục tiêu bài học “Tập hợp, phần tử của tập hợp” đã được cô Vy đề ra như sau:
– Sử dụng được thuật ngữ tập hợp.
– Nhận biết được một phần tử thuộc (không thuộc) một tập hợp.
– Sử dụng được các kí hiệu ∈, ∉ để biểu diễn mối quan hệ phần tử thuộc, không thuộc tập hợp.
– Sử dụng được hai cách cho tập hợp.
II/ Nội dung bài học
1. Làm quen với tập hợp
Ở phần kiến thức đầu tiên này, để giúp các bạn học sinh dễ hình dung, cô Vy đã đưa ra 3 ví dụ vô cùng quen thuộc về tập hợp có đi kèm hình ảnh minh họa, đó là:
– Tập hợp các dụng cụ học tập trên bàn
– Tập hợp các ngón trên một bàn tay
– Tập hợp các số tự nhiên có trong hình

2. Các kí hiệu
Cô Vy lựa chọn cả 3 ví dụ ở phần trước để giảng giải, phân tích về các kí hiệu của tập hợp. Học sinh ghi nhớ kĩ để học tốt môn Toán nhé các em.
* Tập hợp các dụng cụ học tập trên bàn
Gọi A là tập hợp các dụng cụ học tập trên bàn.
Ta có: A = {Compa, bút chì, eke, gôm}.
Lúc này, ta nói: Compa, bút chì, eke, gôm là các phần tử của tập hợp A.
* Tập hợp các ngón trên một bàn tay
Gọi B là tập hợp các ngón trên một bàn tay.
Ta có: B = {Ngón cái, ngón trỏ, ngón giữa, ngón áp út, ngón út}.
Lúc này, ta nói: Ngón cái, ngón trỏ, ngón giữa, ngón áp út, ngón út là các phần tử của tập hợp B.

* Tập hợp các số tự nhiên có trong hình
Gọi C là tập hợp các số tự nhiên có trong hình
Ta có: C = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}
Lúc này, ta nói: Mỗi số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 là một phần tử của tập hợp C.
Hay nói cách khác, các số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 thuộc tập hợp C.
Để biểu diễn mối quan hệ “thuộc” này, ta sẽ sử dụng kí hiệu Toán học “∈”.
Ví dụ: 1 thuộc tập hợp C, ta kí hiệu: 1 ∈ C
Lúc này, cô Vy đặt ra câu hỏi mở rộng cho học sinh thử tư duy: “Vậy thì theo các em số 12 có thuộc tập hợp C hay không?”
Bằng mắt thường quan sát, dễ dàng nhận thấy số 12 không có trên bàn phím minh họa, vậy nên số 12 không là phần tử của tập hợp C.
Hay nói cách khác, số 12 không thuộc tập hợp C, ta kí hiệu: 12 ∉ C.
Tương tự, dụng cụ học tập là eke cũng không thuộc tập hợp C, ta kí hiệu: eke ∉ C.
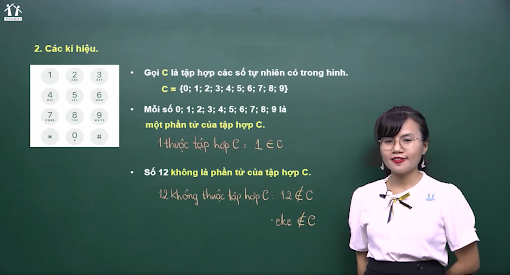
Cô Vy dặn dò học sinh 3 cách ghi tập hợp mà các em cần lưu ý:
– Người ta thường dùng các chữ cái in hoa A, B, C,… để kí hiệu tập hợp, các chữ cái in thường a, b, c,… để kí hiệu phần tử.
– Các phần tử của tập hợp được viết trong dấu { } và cách nhau bởi dấu “,” hay “;” nếu các phần tử là số.
– Mỗi phần tử được liệt kê một lần, thứ tự tùy ý
Ví dụ:
A = {1; 2; 3} = {3; 2; 1}
x thuộc A: x ∈ A
y không thuộc A: y ∉ A
3. Cách cho tập hợp
Vậy liệu có cách nào để viết tập hợp mà không cần phải liệt kê?
Để giúp học sinh tìm hiểu về vấn đề này, cô Vy lấy hình ảnh buổi sinh hoạt chào cờ đầu tuần của trường Tiểu học Đoàn Thị Điểm và đặt ra câu hỏi mở cho các bạn thử tư duy: “Có cách nào viết tập hợp 500 học sinh của trường mà không dùng cách liệt kê?”

Có một cách cho tập hợp khác mà không cần liệt kê, đó là chúng ta sẽ chỉ ra tính đặc trưng cho các phần tử của tập hợp. Ta làm như sau:
Gọi D là tập hợp các học sinh của trường tiểu học Đoàn Thị Điểm.
Ta có: D = {x | x là học sinh của trường tiểu học Đoàn Thị Điểm}.
Vậy là ta đã ghi lại tập hợp D bằng cách chỉ ra tính đặc trưng cho các phần tử x của tập hợp D.
Ví dụ:
B là tập hợp các số tự nhiên nhỏ hơn 6. Ta sẽ có 2 cách để viết tập hợp B:
– Cách 1: Liệt kê các phần tử của tập hợp
B = {0; 1; 2; 3; 4; 5}
– Cách 2: Chỉ ra tính đặc trưng cho các phần tử của tập hợp
B = {x | x là số tự nhiên và x < 6}
4. Bài tập chiếm lĩnh kiến thức
Ở phần này, học sinh cùng thực hiện một số bài luyện tập cùng cô Vy để củng cố và ghi nhớ kiến thức bài học.
Câu 1: Cho tập hợp A gồm các số tự nhiên khác 0 và chia hết cho 3 nhưng nhỏ hơn 10. Phần tử nào sau đây thuộc tập hợp A?
A. 1 B. 5 C. 6 D. 12
Giải
Tập hợp A gồm các số tự nhiên khác 0 và chia hết cho 3 nhưng nhỏ hơn 10.
Ta có: A = {3; 6; 9}
Vậy đáp án chính xác là đáp án C.
Câu 2: Gọi D là tập hợp các chữ cái có trong từ “chăm chỉ”. Hãy biểu diễn tập hợp D.
A. D = {c, h, ă, m, c, h, i}
B. D = {c, ă, h, m, i}
C. D = {c, h, ă, m, h}
D. D = {c, h, m, c, h, i}
Giải
Liệt kê các phần tử của tập hợp D, ta được: D = {c, h, ă, m, i}.
Cô Vy giảng giải: “Mỗi phần tử trong tập hợp chỉ liệt kê một lần”. Do vậy, trong tập hợp D chỉ có 1 chữ “c” và 1 chữ “h”.
Đáp án chính xác là đáp án B.
Câu 3: Cho tập hợp N = {7; 14; 21}. Hãy biểu diễn tập N bằng cách chỉ ra tính đặc trưng cho các phần tử của tập hợp N.
A. N = {x | x là các số tự nhiên khác 0 chia hết cho 7 và x < 21}
B. N = {x | x là các số tự nhiên khác 0 chia hết cho 7}
C. N = {x | x là các số tự nhiên khác 0 chia hết cho 7 và x < 22}
Giải
Ở câu này, ta sẽ xét từng đáp án để tìm ra câu trả lời:
Với đáp án A, x < 21, mà trong tập hợp N có chứa phần tử 21. Do đó A là đáp án sai.
Với đáp án B, chỉ nói rằng x là các số tự nhiên khác 0 chia hết cho 7. Ta lấy ví dụ số 35 cũng là số tự nhiên khác 0 chia hết cho 7, nhưng 35 ∉ N. Do đó B là đáp án sai vì thiếu thông tin.
Với đáp án C, x là các số tự nhiên khác 0 chia hết cho 7 và x < 22. Đáp án C đã chỉ ra được tính đặc trưng cho các phần tử của tập hợp N.
Đáp án chính xác là C.
Câu 4: Cho tập hợp P gồm các số tự nhiên lớn hơn hoặc bằng 8 và nhỏ hơn 16. Gọi Q là tập hợp các số lẻ thuộc tập hợp P. Hãy biểu diễn tập Q.
A. Q = {8; 9; 10; 11; 12; 13; 14; 15}
B. Q = {9; 11;13; 15}
C. Q = {8; 9; 10; 11; 12; 13; 14; 15; 16}
D. Q = {8; 10; 12; 14}
Giải
Tập hợp P gồm các số tự nhiên lớn hơn hoặc bằng 8 và nhỏ hơn 16.
Ta có: P = {8; 9; 10; 11; 12; 13; 14; 15}
Q là tập hợp các số lẻ thuộc tập hợp P.
Do đó, ta có: Q = {9; 11;13; 15}
Đáp án chính xác là B.
Câu 5: Gọi K là tập hợp các thiên thể quay quanh Mặt Trời. Các thiên thể này được gọi là các hành tinh. Hỏi tập hợp K có bao nhiêu phần tử?
A. 5 phần tử
B. 6 phần tử
C. 7 phần tử
D. 8 phần tử
Giải
Cô Vy chia sẻ: “Các em hoàn toàn có thể giải quyết bài toán này bằng cách tìm kiếm thông tin từ các sách khoa học, trên internet,…”
K là tập hợp các thiên thể quay quanh Mặt Trời. Do đó ta có:
K = {Sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương}.
Vậy K có 8 phần tử. Câu trả lời đúng là đáp án D.

Cuối phần nội dung bài học, cô Vy không quên dặn dò các bạn học sinh phần kiến thức trọng tâm cần ghi nhớ kĩ: “Để viết một tập hợp thường có hai cách. Chúng mình có thể liệt kê các phần tử của tập hợp, hoặc cũng có thể chỉ ra tính đặc trưng cho các phần tử của tập hợp đó”.

5. Mở rộng và khám phá
5.1. Em có biết
Ở phần mở rộng và khám phá, cô Vy giới thiệu với học sinh về nhà toán học Cantor. Theo đó, nhà toán học Cantor sinh năm 1845 và mất năm 1918. Lí thuyết tập hợp được phát triển nhờ các nghiên cứu của ông. Từ đó, lí thuyết tập hợp đã nhanh chóng trở thành nền tảng của toán học hiện đại.

Tiếp theo, cô Vy đưa ra một số ví dụ về tập hợp, học sinh cùng theo dõi:

Quan sát hình 1, ta thấy tập hợp A chỉ có 1 phần tử; tập hợp B có 5 phần tử.

Quan sát tiếp hình 2, ta sẽ thấy tập hợp N có vô số phần tử và tập hợp C không chứa phần tử nào. Lúc này, tập hợp C gọi là tập hợp rỗng, kí hiệu C = Ø

Ở hình 3, có 2 bể cá, kí hiệu là bể 1 và bể 2.
Gọi E, F lần lượt là tập hợp các con cá trong bể cá 1 và bể cá 2. Ta có:
E = {cá vàng}. Tập hợp E có 1 phần tử.
Tập hợp F là tập hợp rỗng vì không có con cá nào trong bể, nên: F = Ø
Lúc này, cô Vy rút ra kết luận: “Một tập hợp có thể không có phần tử nào, có thể có 1 phần tử, nhiều hơn 1 phần tử, hoặc cũng có thể có vô số phần tử”.
5.2. Sơ đồ Venn
Cô Vy giới thiệu thêm cho học sinh về sơ đồ Venn. Ngoài 2 cách biểu diễn tập hợp là liệt kê các phần tử và chỉ ra tính đặc trưng cho các phần tử đã nêu ở trên thì ta cũng có thể minh họa tập hợp bằng một vòng tròn khép kín. Theo đó, các phần tử của tập hợp sẽ được biểu diễn bằng các chấm trong vòng khép kín đó.
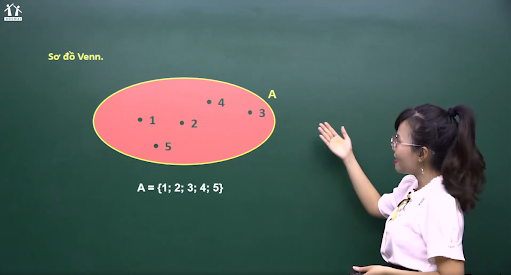
Nhìn vào hình vẽ, ta có thể nhận biết được các phần tử của tập hợp A:
A = {1; 2; 3; 4; 5}
Trên đây là những hướng dẫn của cô Lê Khánh Vy trong bài học về “Tập hợp, phần tử của tập hợp”, bộ môn Toán 6, sách Chân trời sáng tạo. Năm học mới đã chính thức bắt đầu, phụ huynh có con vừa vào cấp hai còn đang băn khoăn, lo lắng về những đổi mới trong Chương trình Giáo dục phổ thông mới của Bộ Giáo dục và Đào tạo thì có thể tham khảo Chương trình Học tốt lớp 6 mới của HOCMAI. Chương trình sẽ là giải pháp học tập toàn diện giúp teen 2k10 được trang bị kiến thức đầy đủ, sẵn sàng trước những thay đổi trong năm học mới này.
Để biết thêm thông tin chi tiết về khóa học, phụ huynh và học sinh hãy liên hệ Hotline 093 658 5812 hoặc ĐĂNG KÝ NGAY TẠI ĐÂY để được TƯ VẤN MIỄN PHÍ!


















