Lời giải “Bài toán diện tích không biên giới” – thầy Trần Phương (video)

Thầy Trần Phương, tác giả bài toán diện tích không giới hạn đã đưa ra lời giải chi tiết cùng chia sẻ thú vị về nguồn gốc của bài toán.

Bài toán diện tích không biên giới được ra đời vào năm 1998 trong vòng chung kết của chương trình “7 sắc cầu vồng”. Khi đó, với vai trò cố vấn Toán học cho chương trình, thầy Trần Phương đã trăn trở để tìm ra một bài toán đảm bảo độ hay, hấp dẫn và có thể giải quyết nhanh gọn cho vòng chung kết toàn quốc. Ý tưởng lóe lên khi thầy nhìn thấy tia nắng chiếu qua khe cửa sổ, thầy đã suy nghĩ về việc tia nắng rõ ràng rất mảnh nhưng dải tia nắng diện tích lại vô cùng lớn, vậy có thể có hay không tam giác rất hẹp mà diện tích lớn hơn trái đất? Khi đó bài toán đã ra đời:

Lời giải:

Sai lầm thường gặp hay trực giác đánh lừa tư duy:

TOPCLASS 2024 - CHƯƠNG TRÌNH HỌC TOÀN DIỆN

NẮM CHẮC KIẾN THỨC - BỨT PHÁ ĐIỂM SỐ

• Chu trình học tập khép kín HỌC - LUYỆN - HỎI - KIỂM TRA
• Đa dạng hình thức học - Phù hợp với mọi nhu cầu
• Đội ngũ giáo viên giảng dạy nổi tiếng với 16+ năm kinh nghiệm
• Dịch vụ hỗ trợ học tập đồng hành xuyên suốt quá trình học tập

Ưu đãi đặt chỗ sớm - Giảm đến 45%! Áp dụng cho PHHS đăng ký trong tháng này!

HỌC THỬ MIỄN PHÍ ĐĂNG KÝ NGAY

Cảm nhận đầu tiên của chúng ta là không thể có tam giác nào thỏa mãn các điều kiện của đề bài. Thật vậy, khi ta vẽ một tam giác cho trước với các độ dài đường cao nào đấy, rồi để cho các độ dài đường cao thu nhỏ hơn 1 mm thì trực giác sẽ đưa chúng ta hướng đến thao tác bóp tam giác thu nhỏ dần để nó tiến về một điểm. Nhưng khi đó, diện tích của tam giác sẽ tiến đến 0 và chắc chắn nhỏ hơn so với diện tích trái đất là 510.100.000 km2.

Trực giác làm bừng sáng tư duy

Có một sự ngẫu nhiên trùng hợp khi quả táo rơi, Newton đã phát minh ra định luật “Vạn vật hấp dẫn”. Còn bài toàn này được ra đời khi có một tia nắng chiếu qua khe cửa sổ rọi đến mắt tác giả làm bừng lên một ý tưởng “Độ rộng của tia nắng rất hẹp nhưng diện tích của dải tia nắng kia lại rất lơn vì tia nắng xuất phát từ mặt trời có khoảng cách rất xa so với trái đất”. Và tam giác cần tìm là tam giác được đặt trong dải tia nắng rất hẹp ấy.

Từ trực giác đến ý tưởng toán học

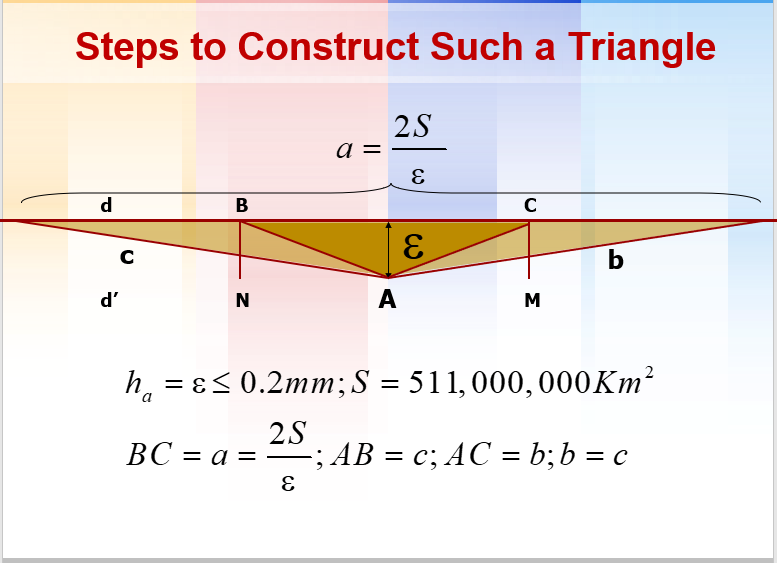
Chúng ta hãy vẽ đường thẳng (d), sau đó tịnh tiến (d) một khoảng ε nhỏ tùy ý để nhận được (d’). Khi đó, diện tích của dải mặt phẳng tạo bởi 2 đường thẳng song song (d), (d’) là một đại lượng vô cùng lớn.

Nếu ta đặt hình chữ nhật BCMN nằm trong dải mặt phẳng tạo bởi (d) và (d’) thì khi dịch chuyển 2 cạnh BN, CM về 2 đầu của dải phẳng, tức là tăng chiều dài BC, MN, diện tích hình chữ nhật BCMN sẽ có số đo vô cùng lớn.

Lấy tam giác ABC nội tiếp trong hình chữ nhật BCMN thì diện tích (ABC) bằng một nửa diện tích (BCMN) nên cũng có số đo vô cùng lớn. Ta chỉ cần chứng minh khi đó tổng độ dài 3 dường cao của tam giác ABC nhỏ tùy ý.

Đặc biệt hóa để đánh giá tổng độ dài ba đường cao

Để thuận tiện, ta chọn A là trung điểm của MN. Khi đó tam giác ABC cân tại A.

Ta có:

Dựng tam giác có diện tích vô cùng lớn và tổng ba đường cao vô cùng bé

Vẽ một đường thẳng (d) cho trước. Tịnh tiến (d) một khoảng ε nhỏ tùy ý, chẳng hạn ε<0,2mm để nhận được đường thẳng (d’)//(d).

Đặt S = 511.000.000 km2. Trên (d) lấy 2 điểm B, C sao cho BC=2S/ε.

Lấy điểm A∈(d’) sao cho tam giác ABC cân tại A.

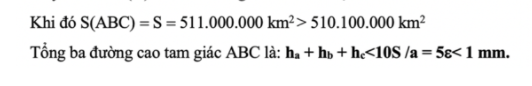
“Như vậy, ta đã chỉ ra có vô số tam giác có tổng độ dài ba đường cao nhỏ tùy ý nhưng diện tích của nó lớn tùy ý. Tính chất của tam giác làm chúng ta liên tưởng đến Covid-19 chủng virus rất bé nhỏ nhưng gây ra đại dịch vô cùng lớn ảnh hưởng đến toàn cầu” – thầy Trần Phương kết luận.