Hàm số và đồ thị hàm số là một trong những kiến thức quan trọng trong Toán 9, đặc biệt luôn xuất hiện trong các đề thi học kỳ, đề thi vào 10. Để nắm chắc các kiến thức cũng như kỹ năng làm bài thi đạt điểm cao, học sinh cùng ôn tập với thầy Lưu Huy Thưởng trong video bài giảng dưới đây nhé!
Xem video bài giảng để biết thêm chi tiết:
I. Hàm số
1. Ví dụ mở đầu
Cho thời gian t, công thức s = 5.t², hãy tính thời gian s với dữ kiện trong bảng dưới:
|
t |
1 | 2 | 3 | 4 | 5 |
| s | 5 | 20 | 45 | 80 |
125 |
=> Từ đó ta rút ra được hàm số: y=a.x².
2. Tính chất của hàm số y = a.x² (a≠0)
Xét 2 hàm số: y= 2.x² và y= -2.x²:
a, Hàm số y= 2.x²
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 18 | 8 | 2 | 0 | 2 | 8 | 18 |
Nhận xét:
- Khi giá trị x tăng (luôn âm) giá trị y giảm.
- Khi giá trị x tăng (luôn dương) giá trị y tăng.

Nhận xét các ví dụ về hàm số.
b, Hàm số y= -2.x²
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 18 | 8 | 2 | 0 | 2 | 8 | 18 |
Nhận xét:
- Khi x tăng (luôn âm) giá trị y tăng.
- Khi x tăng (luôn âm) giá trị y giảm.
3. Kết luận
– Với hàm số y=a.x²:
- Nếu a>- thì hàm số nghịch biến khi x<0 và đồng biến khi x>0.
- Nếu a<0 thì hàm số nghịch biến khi x>0 và đồng biến khi x<0.
– Tính chất:
+ a>0 -> y>0 với mọi x≠0.
x=0 -> y=0 là giá trị nhỏ nhất của hàm số.
+ a<0 -> y=0 với mọi x≠0.
x=0 -> y=0 là giá trị lớn nhất của hàm số.
II. Đồ thị hàm số y= a.x² (a ≠ 0)
1. Khảo sát hàm số y= x²
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Từ đó ta có các điểm A(-3;9), B(-2;4), C(-1;1), A’(3,9), B’(2;4), C’(1;1), D(0;0) vẽ được đồ thị hàm số y= x².
Nhận xét:
- Đồ thị hàm số nằm hoàn toàn phía trên trục Ox.
- Các cặp điểm A và A’, B và B’, C và C’ đối xứng qua Oy.
- Điểm thấp nhất của đồ thị hàm số là gốc tọa độ O(0;0).
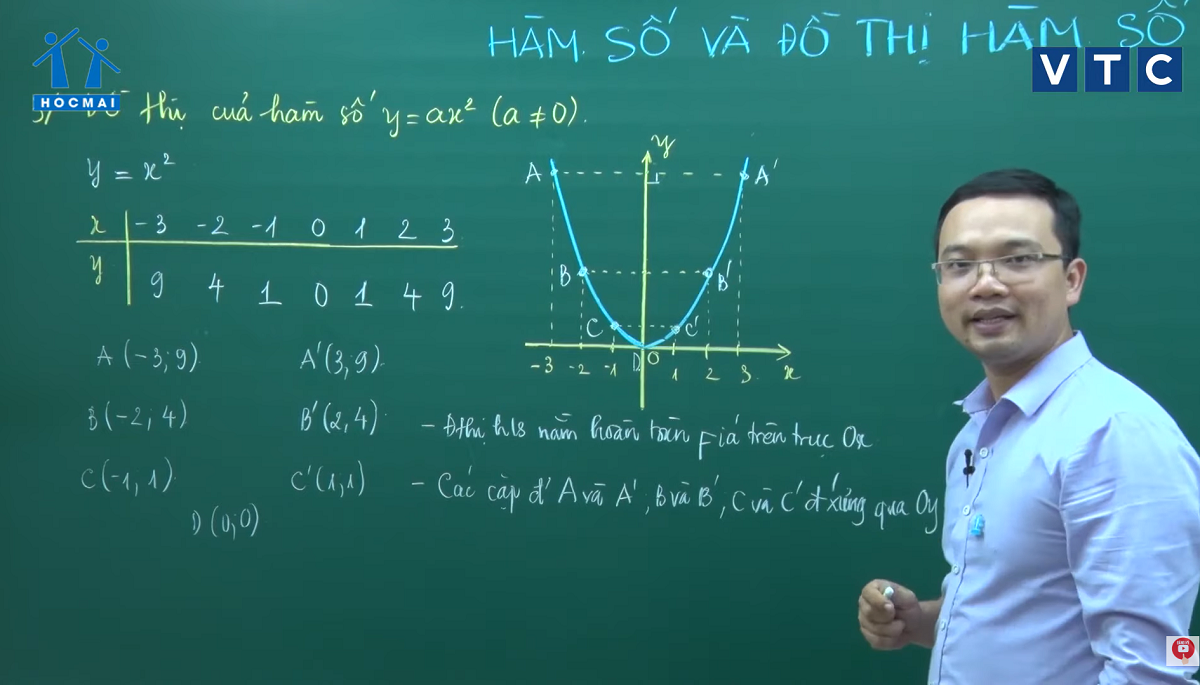
Vẽ đồ thị hàm số.
2. Khảo sát hàm số y=-x²
|
x |
-3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -9 | -4 | -1 | 0 | -1 | -4 |
-9 |
Từ đó ta có các điểm A(-3;-9), B(-2;-4), C(-1;1), A’(3,-9), B’(2;-4), C’(1;-1), D(0;0) vẽ được đồ thị hàm số y=x2.
Nhận xét:
- Đồ thị hàm số nằm hoàn toàn phía dưới trục Ox.
- Các cặp điểm A và A’, B và B’, C và C’ đối xứng qua Oy.
- Điểm cao nhất của đồ thị hàm số là gốc tọa độ O(0;0).
3. Kết luận chung
– Đồ thị của hàm số là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol với đỉnh O.
– Nếu a>0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị hàm số.
– Nếu a<0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị hàm số.
4. Cách vẽ đồ thị hàm số y= ax2
– Tìm tập xác định R.
– Lập bảng giá trị.
– Vẽ đồ thị.
Chú ý: Đồ thị hàm số nhận trục Oy làm trục đối xứng nên khi vẽ ta chỉ cần lấy các điểm bên phải Oy sau đó lấy các điểm đối xứng với chúng qua Oy.
III. Luyện tập
Ví dụ: Cho hàm số y= a.x² có đồ thị đi qua điểm (2;1):
a, Tìm hệ số a và vẽ đồ thị hàm số.
b. Tìm điểm thuộc Parabol nói trên có hoành độ bằng -3.
c, Tìm điểm thuộc Parabol nói trên có hoành độ bằng ¾ .
Bài giải:
a, Đồ thị hàm số y= ax² đi qua điểm (2;1):
=> 1 = a. 2² <=> a = ¼ .
=> hàm số y = ¼ x².
– Tập xác định R.
– Bảng giá trị:
|
x |
-3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 9/4 | 1 | 1/4 | 0 | 1/4 | 1 |
9/4 |
– Vẽ đồ thị.

Giải bài tập
b, Ta có: y= ¼ .x².
x= -3 -> y.(-3) =9/4.
Điểm cần tìm (-3;9/4).
c, Ta có: y = 9/4 -> ¼ . x² = 9/4.
⇔ x² = 9.
⇔ x = ±3.
Điểm cần tìm (-3;9/4).
Trên đây là những kiến thức trọng tâm của hàm số bậc hai và đồ thị hàm số. Để đảm bảo việc học tại nhà hiệu quả, lượng kiến thức không bị gián đoạn, đứt gãy, phụ huynh và các bạn học sinh hãy tham khảo thêm nhiều kiến thức mới trước khi quay lại trường, phụ huynh có thể tham khảo ngay Chương trình Học Tốt 2021 – 2022 tại HOCMAI cho con em mình.
Chương trình gồm hệ thống bài giảng chi tiết, chất lượng, bám sát chương trình học của Bộ GD&ĐT. Bên cạnh đó là kho bài tập phong phú, đa dạng, có các dịch vụ hỗ trợ tiện ích không chỉ giúp học sinh học hành thuận tiện mà còn giúp phụ huynh dễ dàng kiểm tra, đánh giá được tình hình học tập của con.
>>> Đăng ký học thử miễn phí TẠI ĐÂY.
Thông tin chi tiết liên hệ ngay hotline 0936 5858 12 để được tư vấn miễn phí.


















