Phương pháp phân tích đa thức thành nhân tử trong Toán đại số 8 (học kỳ I) là một dạng toán tương đối khó, bởi đây là kiến thức để vận dụng cho những chương trình học ở lớp trên. Vì vậy mà trong bài viết dưới đây, HOCMAI sẽ gửi tới các bạn học sinh – 6 cách phân tích đa thức thành nhân tử thường được sử dụng trong chương trình Toán lớp 8.

Phương pháp phân tích đa thức thành nhân tử Toán 8.
1. Phương pháp đặt nhân tử chung
– Tìm nhân tử chung là những đơn, đa thức có mặt trong tất cả các hạng tử.
– Phân tích mỗi hạng tử thành tích của nhân tử chung và một nhân tử khác.
– Viết nhân tử chung ra ngoài dấu ngoặc, viết các nhân tử còn lại của mỗi hạng tử vào trong dấu ngoặc (kể cả dấu của chúng). Để dễ hiểu chúng ta có như sau:
A.B + C.B – B.Q=B.(A + C-Q)

Những phép tính sử dụng phương pháp đặt nhân tử chung
2. Phương pháp dùng hằng đẳng thức
Vận dụng các hằng đẳng thức để biến đổi đa thức thành tích các nhân tử hoặc lũy thừa của một đa thức đơn giản.
Ví dụ: Phân tích các đa thức sau thành nhân tử.
9×2 – 4 = (3x)2 – 22 = ( 3x– 2)(3x + 2)
8 – 27a3b6 = 23 – (3ab2)3 = (2 – 3ab2)( 4 + 6ab2 + 9a2b4)
25×4 – 10x2y + y2 = (5×2 – y)2
3. Phương pháp tách một hạng tử thành nhiều hạng tử
- Nếu đa thức f(x) có nghiệm hữu tỉ thì nghiệm có dạng p/q. Trong đó p là ước của hệ số tự do, q là ước dương của hệ số cao nhất.
- Nếu đa thức f(x) có tổng các hệ số bằng 0 thì f(x) có một nhân tử là x–1.
- Nếu đa thức f(x) có tổng các hệ số của các hạng tử bậc chẵn bằng tổng các hệ số của các hạng tử bậc lẻ thì f(x) có một nhân tử là x+1
- Nếu a là nghiệm nguyên của đa thức f(x) và f(1); f(−1) khác 0 thì f(1)/a−1 và f(−1)/a+1 đều là số nguyên. Để nhanh chóng loại trừ nghiệm là ước của hệ số tự do.
Ví dụ: x^2 – 5x + 6 = x^2 – 2x- 3x + 6 (tách 5x = 2x + 3x)
= x (x- 2) – 3(x- 2)
= (x-2)(x- 3)
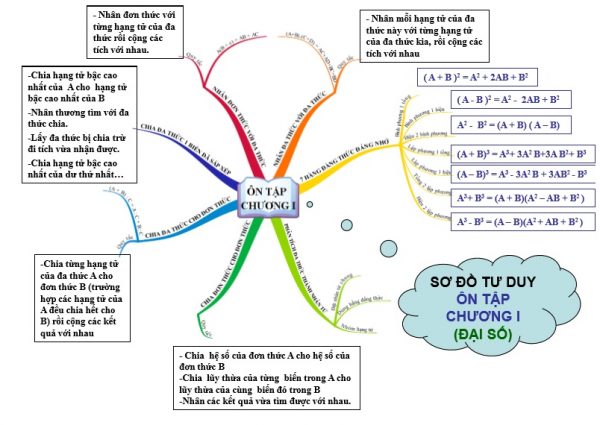
Tóm tắt kiến thức chương 1 Toán 8 bằng sơ đồ tư duy
4. Phương pháp thêm, bớt cùng một hạng tử
Để sử dụng phương pháp này, ta có thể thêm bớt 1 hạng tử nào đó của đa thức để làm xuất hiện những nhóm hạng tử mà ta có thể dùng các phương pháp khác để phân tích được.
Trường hợp 1: Thêm, bớt cùng một số hạng tử để xuất hiện hiệu hai bình phương:
Ví dụ: 4×4 + 81 = 4×4 + 36×2 + 81 – 36×2 = (2×2 + 9)2 – 36×2
= (2×2 + 9)2 – (6x)2 = (2×2 + 9 + 6x)(2×2 + 9 – 6x)
= (2×2 + 6x + 9 )(2×2 – 6x + 9)
Trường hợp 2: Thêm, bớt cùng một số hạng tử để xuất hiện nhân tử chung
Ví dụ: x7 + x2 + 1 = (x7 – x) + (x2 + x + 1 ) = x(x6 – 1) + (x2 + x + 1 )
= x(x3 – 1)(x3 + 1) + (x2 + x + 1 ) = x(x – 1)(x2 + x + 1 ) (x3 + 1) + (x2 + x + 1)
= (x2 + x + 1)[x(x – 1)(x3 + 1) + 1] = (x2 + x + 1)(x5 – x4 + x2 – x + 1)
Trong một số trường hợp, để việc phân tích đa thức thành nhân tử được thuận lợi, ta phải đặt biến phụ thích hợp.
Ví dụ: x(x + 4)(x + 6)(x + 10) + 128 = [x(x + 10)][(x + 4)(x + 6)] + 128
= (x2 + 10x) + (x2 + 10x + 24) + 128
Đặt x2 + 10x + 12 = y, đa thức có dạng
(y – 12)(y + 12) + 128 = y2 – 144 + 128 = y2 – 16 = (y + 4)(y – 4)
= ( x2 + 10x + 8 )(x2 + 10x + 16 ) = (x + 2)(x + 8)( x2 + 10x + 8 )
6. Phương pháp phối hợp nhiều phương pháp
Chọn các phương pháp theo thứ tự ưu tiên:
– Đặt nhân tử chung.
– Dùng hằng đẳng thức.
– Nhóm nhiều hạng tử.
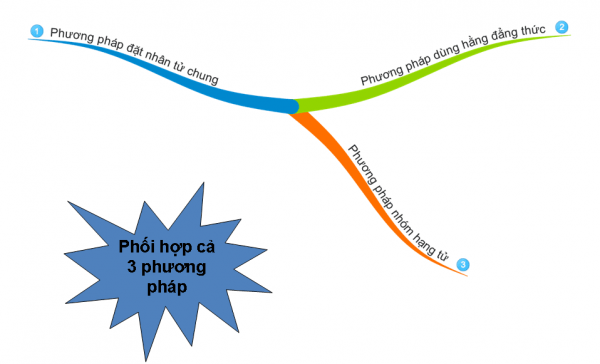
Phối hợp cả 3 phương pháp.
Ví dụ: Phân tích các đa thức sau thành nhân tử
3xy2 – 12xy + 12x = 3x(y2 – 4y + 4) = 3x(y – 2)2
3x3y – 6x2y – 3xy3 – 6axy2 – 3a2xy + 3xy = 3xy(x^2– 2x – y^2 – 2ay – a^2 + 1)
= 3xy[( x2 – 2x + 1) – (y2 + 2ay + a2)]
= 3xy[(x – 1)2 – (y + a)2]
= 3xy[(x – 1) – (y + a)][(x – 1) + (y + a)]
= 3xy( x –1 – y – a)(x – 1 + y + a)
Trên đây là 6 cách phân tích đa thức thành nhân tử mà chúng ta có thể gặp. Tuy nhiên, để áp dụng cụ thể từng phương pháp trên vào giải quyết các bài tập khó ngay tại nhà, thì các bạn học sinh lớp 8 cần tham khảo thêm các bài giảng online Toán 8 nằm trong Chương trình Học tốt 2019 – 2020 tại HOCMAI.
Chương trình được thiết kế với 01 khóa Trang bị kiến thức và 01 khóa Ôn luyện nhằm giúp học sinh nắm vững kiến thức sách giáo khoa, hiểu sâu kiến thức nền tảng. Từ đó, sử dụng thành thạo các phương pháp phân tích đa thức thành nhân tử thông qua những ví dụ cụ thể trong bài giảng của những thầy cô giáo trẻ, giàu kinh nghiệm, đến từ các trường THCS nổi tiếng trên địa bàn thành phố Hà Nội.
Phụ huynh và học sinh để lại thông tin TẠI ĐÂY, sẽ nhận được tư vấn miễn phí về các khóa học online tại HOCMAI.
>>>ĐĂNG KÝ MIỄN PHÍ: http://bit.ly/da-thuc-nhan-tu-8



















