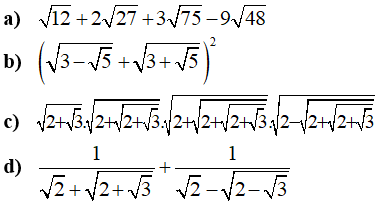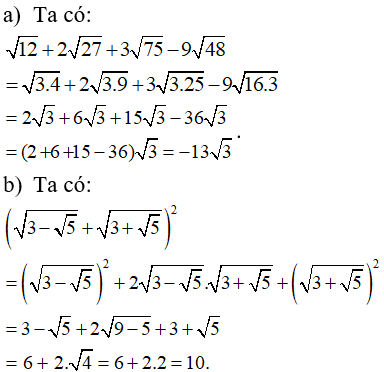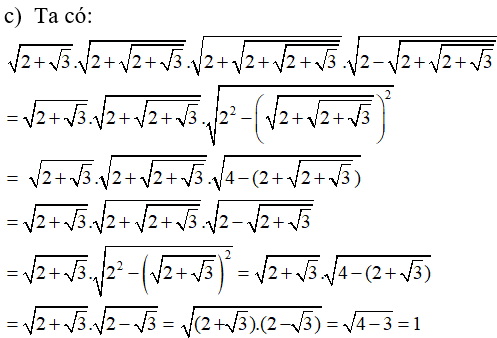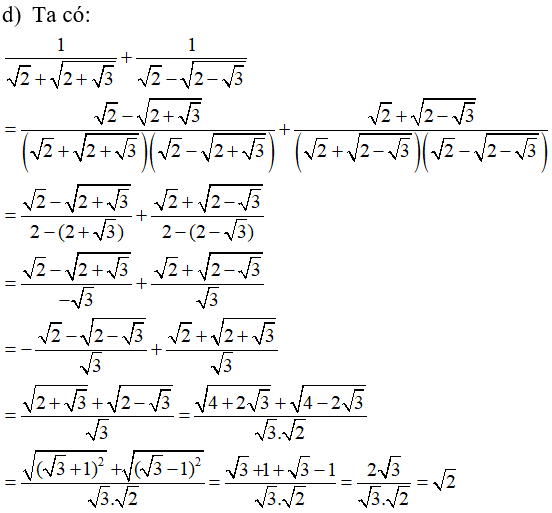Liên hệ giữa phép nhân và phép khai phương – Toán lớp 9

18/05/2022

1089

Liên hệ giữa phép nhân và phép khai phương là lý thuyết quan trọng trong chương trình toán lớp 9 và thường xuyên xuất hiện trong các đề thi học kỳ, đề thi vào lớp 10 với các mức độ trải dài từ dễ đến khó. Chính vì thế HOCMAI chia sẻ cho các em học sinh những kiến thức cơ bản cần nẵm rõ về bài này cũng như các dạng bài tập thường xuyên gặp.

A. Lý thuyết về liên hệ giữa phép nhân và phép khai phương

1. Căn bậc hai của một tích

Cho 2 biểu thức A và B (điều kiện A và B đều không âm), ta có biểu thức sau:

√(A x B) = √A x √B

Lưu ý:

– Ngoài áp dụng cho biểu thức thì công thức trên còn áp dụng được với 2 số a và b (điều kiện a và b đều không âm)

– Để áp dụng biểu thức trên bắt buộc cả 2 số hoặc biểu thức A và B đều không âm. Ví dụ: Ta có √(-20 x -30) nhưng ta √(-20) x √(-30) lại không xác định.

Một số bài tập ví dụ về phép nhân:

Tính √36

Hướng dẫn giải: √36 = √(4 x 9) = √4 x √9 = 2 x 3 = 6

Tính √200

Hướng dẫn giải: √200 = √(100 x 2) = √100 x √2 = 10√2

Tính √(1 x 625)

Hướng dẫn giải: √(1 x 625) = √1 x √625 = 1 x 25 = 25

Tính √(4 x 81)

Hướng dẫn giải: √(4 x 81) = √4 x √81 = 2 x 9 = 18

2. Phương pháp và các trường hợp áp dụng công thức trên

+ Quy tắc khai phương của một tích

Muốn khai phương một tích bao gồm các số hay các biểu không âm, ta hoàn toàn có thể khai phương của từng thừa số hay từng biểu thức rồi sau đó nhân các kết quả lại với nhau.

+ Quy tắc nhân các căn bậc 2 với nhau

Khi nhân hay nhiều căn bậc hai của các số hay các biểu thức không âm với nhau, ta có thể nhân các số hay các biểu thức dưới căn với nhau rồi thực hiện phương pháp khai phương kết quả đó.

Trọn bộ tài liệu các dạng bài, đề thi miễn phí tại: Tài liệu ôn tập toán 9

B. Các dạng bài tập áp dụng lý thuyết về liên hệ giữa phép nhân và phép khai phương

Dạng bài 1: Thực hiện phép tính

Sử dụng: Với hai biểu thức hoặc 2 số không âm A và B, ta có: √(A x B) = √A x √B

Ví dụ:

Bài 1: Tính √50 + √18

Giải: √50 + √18 = √25.2 + √9.2 = √25.√2 + √9.√2 = 5√2 + 3√2 = 8√2

Bài 2: Tính giá trị các phép tính sau:

HM10 2024 - GIẢI PHÁP LUYỆN THI TOÀN DIỆN

NẮM CHẮC KIẾN THỨC - KHÔNG LO BIẾN DỘNG ĐỀ THI

Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP