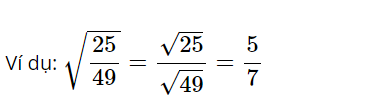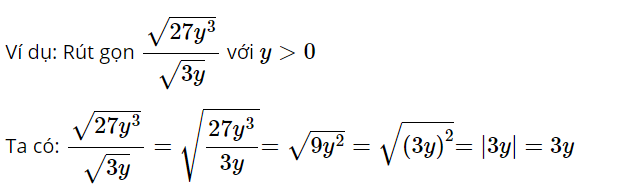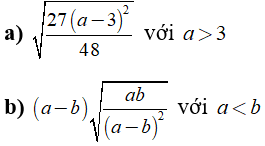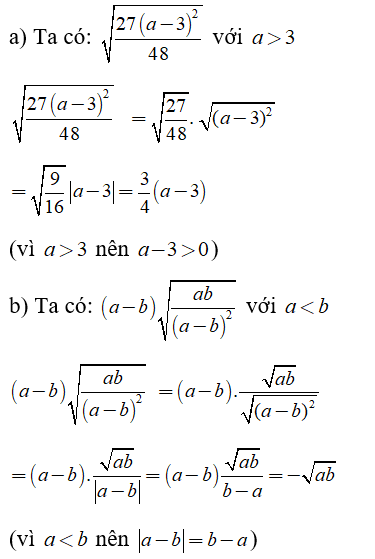Giống như phép nhân, liên hệ giữa phép chia và phép khai phương là một trong những phần lý thuyết quan trọng trong chương trình toán lớp 9 và xuất hiện rất nhiều trong các dạng bài tập khác nhau. HOCMAI sẽ tổng hợp và chia sẻ một cách ngắn gọn nhất nội dung phần này, từ đó giúp các em học sinh có cái nhìn tổng quan nhất.
A. Lý thuyết liên hệ giữa phép chia và phép khai phương
1. Định lý:
Với A và B là 2 số hoặc biểu thức không âm ta có: √(A/B) = √A/√B
Điều kiện để biểu thức trên xác định khi và chỉ khi: A ≥ 0 và B > 0
2. Áp dụng liên hệ giữa phép chia và phép khai phương
+ Quy tắc khai phương của một thương
Nếu muốn khai phương một thương có a/b thỏa mã điều kiện số a không âm và số b dương khác 0. Khi đó, ta có thể lần lượt khai căn các phần tử a và b (bao gồm cả số và biểu thức). Sau đó lấy kết quả thu được chia cho nhau. Cụ thể
√(A/B) = √A/√B
+ Quy tắc chia hai căn bậc hai
Khi chia hai căn bậc hai của số a không âm và số b dương khác 0, ta có thể thực hiện phép tính lấy số a chia cho số b rồi thực hiện phương pháp khai phương kết quả vừa tìm được.
√a/√b = √(a/b)
B. Một số dạng bài tập thường gặp về liên hệ giữa phép chia và khai phương
Dạng 1: Tính giá trị của biểu thức
Phương pháp giải: Với biểu thức A không âm và biểu thức B dương khác không ta có:
√(A/B) = √A/√B
Dạng 2: Rút gọn biểu thức đã cho
Phương pháp giải: Với biểu thức A không âm và biểu thức B dương khác không ta có:
√A/√B = √(A/B)
Bài tập thực hành:
Bài tập 1: Rút gọn biểu thức sau:
Giải:
Bài tập 2: Giải phương trình sau:
Giải:
Tham khảo thêm:
