Bảng căn bậc 2 thuộc chương trình toán lớp 9 giúp các em học sinh có thể tính căn bậc 2 của một số bất kỳ mà không cần sử dụng đến máy tính. Hãy cùng HOCMAI tìm hiểu cách sử dụng.
A. Lý thuyết về bảng căn bậc 2
1. Giới thiệu về bảng căn bậc 2
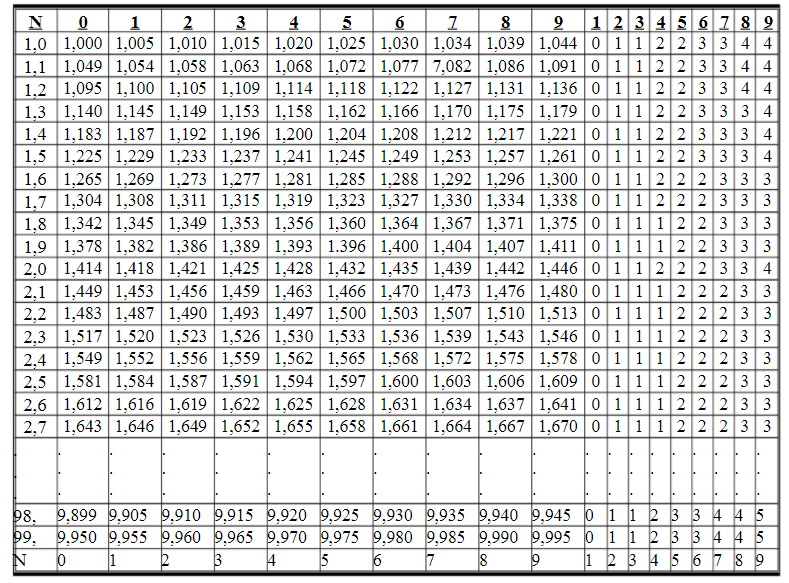
+ Bảng căn bậc 2 có cấu tạo bao gồm các hàng và các cột
+ Cấu tạo của căn bậc 2 của các số được tạo bởi không nhiều hơn ba chữ số. Số đầu tiên bắt đầu từ 1,00 đến 99,9 được ghi sẵn trong bảng căn bậc 2 kết hợp với các cột có số bắt đầu từ 0 đến 9.
+ Bảng căn bậc 2 còn bao gồm cột hiệu chính được sử dụng để hiệu chính chữ số cuối của căn bậc hai của các số được viết bởi bốn số bắt đầu từ 1,000 đến 99,99 .
+ Bảng căn bậc 2 chi tiết như sau:
Cách sử dụng bảng căn bậc 2
1. Cách tìm căn bậc 2 của số bất kỳ lớn hơn 1 và nhỏ hơn 100
Để tìm kết quả có 1 số bất kỳ, ta tìm phần nguyên của số đó và sau dấu “,” 1 chữ số trên cột dọc (nếu trên cột dọc có). Sau đó các phần sau sẽ đối chiếu với hàng ngang của cột, giao điểm của cột dọc và cột ngang chính là kết quả của căn bậc 2 của số đó.
Ví dụ:
- Tính kết quả √5,76
Giải: ta đối chiếu với bảng căn bậc 2
Ta sẽ có kết quả √5,76 = 2,400
- Tính √36,72
Giải: Ta đối chiếu với bảng căn bậc 2
Vậy ta có kết quả √36,72 = 6,0582
- Tương tự các em học sinh tra bảng để tìm √9,15 và √40,85
2. Cách tìm căn bậc 2 của số lớn hơn 100
Để tìm được căn bậc 2 của số lớn hơn 100, ta biến đổi số đó thành phép nhân của các số <100 với nhau, sau đó dùng bảng căn bậc 2 tính căn bậc 2 của từng số đã biến đổi và nhân với nhau để ra kết quả.
Ví dụ:
- Tính √2006
Giải: √2006 = √(20,06×100) = √20,06 x √100 = 10 x √20,06
Tra bảng căn bậc 2 ta có √20,06 = 4,539
Vậy √2006 = 10 x 4,539 = 45,39
c) Cách tính căn bậc hai của số nhỏ hơn 1 và không âm
Tương tự như cách tìm căn bậc 2 của số lớn hơn 100 tính căn bậc 2 của số nhỏ hơn 1 không âm thì ta lại áp dụng biến đổi dựa trên phép chia. Sử dụng bảng căn bậc 2 để tính từng căn bậc 2 của các số rồi chia cho nhau để ra kết quả.
Ví dụ:
B. Một số bài tập luyện tập sử dụng bảng căn bậc 2
Tham khảo thêm:
Liên hệ giữa phép thương và phép khai phương
