Đường thẳng song song và đường thẳng cắt nhau – Toán lớp 9

HM10 2024 - GIẢI PHÁP LUYỆN THI TOÀN DIỆN

NẮM CHẮC KIẾN THỨC - KHÔNG LO BIẾN DỘNG ĐỀ THI

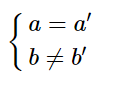
• Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
• ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
• TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
• DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP

Ưu đãi đặt chỗ sớm - Giảm đến 45%! Áp dụng cho PHHS đăng ký trong tháng này!

HỌC THỬ MIỄN PHÍ ĐĂNG KÝ NGAY

TOPCLASS 2024 - CHƯƠNG TRÌNH HỌC TOÀN DIỆN

NẮM CHẮC KIẾN THỨC - BỨT PHÁ ĐIỂM SỐ

• Chu trình học tập khép kín HỌC - LUYỆN - HỎI - KIỂM TRA
• Đa dạng hình thức học - Phù hợp với mọi nhu cầu
• Đội ngũ giáo viên giảng dạy nổi tiếng với 16+ năm kinh nghiệm
• Dịch vụ hỗ trợ học tập đồng hành xuyên suốt quá trình học tập

Ưu đãi đặt chỗ sớm - Giảm đến 45%! Áp dụng cho PHHS đăng ký trong tháng này!

HỌC THỬ MIỄN PHÍ ĐĂNG KÝ NGAY

Đồ thị của 2 đường thẳng song song:

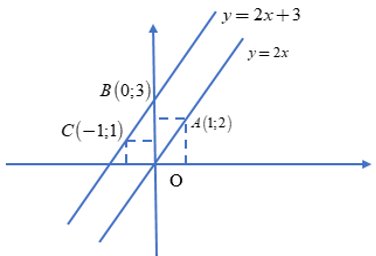
3. Trường hợp 2 đường thẳng cắt nhau

Trường hợp đường thẳng d cắt với d’ khi và chỉ khi:

Đồ thị của 2 đường thẳng cắt nhau

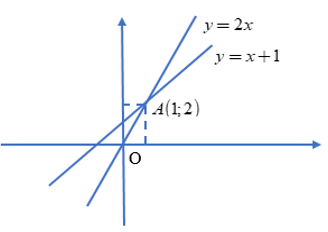
4. Trường hợp 2 đường thẳng trùng nhau

Trường hợp đường thẳng d trùng với d’ khi và chỉ khi:

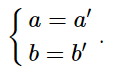
5. Trường hợp 2 đường thẳng vuông góc

Trường hợp đường thẳng d vuông góc với d’ khi và chỉ khi:

a . a’ = -1

Bài tập ví dụ:

• Cho 2 đường thẳng có dạng:

(d): $y=3x+1$

$\mathrm{(d’):\; y}=3x-6$

Do 2 đường thẳng có hệ số a = a’ = 3 và b = 1 ≠ b’ = -6

Vậy 2 đường thẳng d và d’ song song với nhau

• Hai đường thẳng có dạng:

(d): $y=3x+1$

(d’): y = 3x + 1

Do 2 đường thẳng có hệ số a = a’ = 3 và b = b’ = 1

Vậy 2 đường thằng d và d’ trùng nhau

• Hai đường thẳng có dạng

$\mathrm{(d):\; y}=x$

$\mathrm{(d’):\; y}=-2x+3$

Do 2 đường thẳng có hệ số a ≠ a’  và b ≠ b’

Vậy 2 đường thẳng d và d’ giao nhau

B. Các dạng bài tập 2 đường thẳng song song và cắt nhau

Dạng bài tập 1: Chỉ ra được vị trí tương đối của hai đường thẳng cho trước. Tìm tham số m để các đường thẳng thỏa mãn các điều kiện về vị trí tương đối theo đề bài

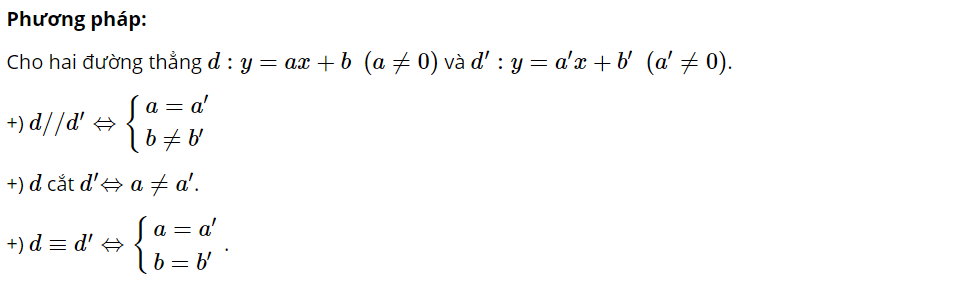
Dạng bài tập 2: Viết phương trình của đường thẳng

Dạng bài tập 3: Tìm điểm cố định mà đường thẳng luôn đi qua khi tham số m thay đổi

Trên đây là toàn bộ lý thuyết và các dạng bài liên quan về đường thẳng song song và đường thẳng cắt nhau thuộc chương trình Toán lớp 9. Hy vọng bài viết trên cung cấp những kiến thức hữu ích cho các em học sinh trong quá trình học cũng như ôn thi vào 10 môn Toán.

Tham khảo thêm:

Nhắc lại và bổ sung các khái niệm về hàm số