Các em học sinh khối 9 thân mến, trong bài viết này HOCMAI muốn giới thiệu với các em học sinh bài tập chứng minh tứ giác nội tiếp đường tròn nằm trong chương trình Toán 9. Sau khi đã nắm vững những kiến thức cơ bản về tứ giác nội tiếp như định nghĩa, định lý, tính chất và dấu hiệu nhận biết thì chúng ta sẽ bắt đầu làm những bài tập này nhé!
Về phương pháp chứng minh tứ giác nội tiếp, các em học sinh có thể tham khảo ngay bài viết:
Phương pháp chứng minh tứ giác nội tiếp
Bài tập chứng minh: Tứ giác nội tiếp đường tròn
Bài 1: Cho bốn điểm A, B, C, D theo thứ tự đó nằm trên đường tròn tâm O; I là điểm chính giữa của cung AB (không chứa C và D); I là điểm chính giữa cung AB (không chứa C và D). IC và AD kéo dài giao nhau tại E; ID kéo dài cắt BC kéo dài tại F. Hãy chứng minh rằng tứ giác CDEF nội tiếp đường tròn.
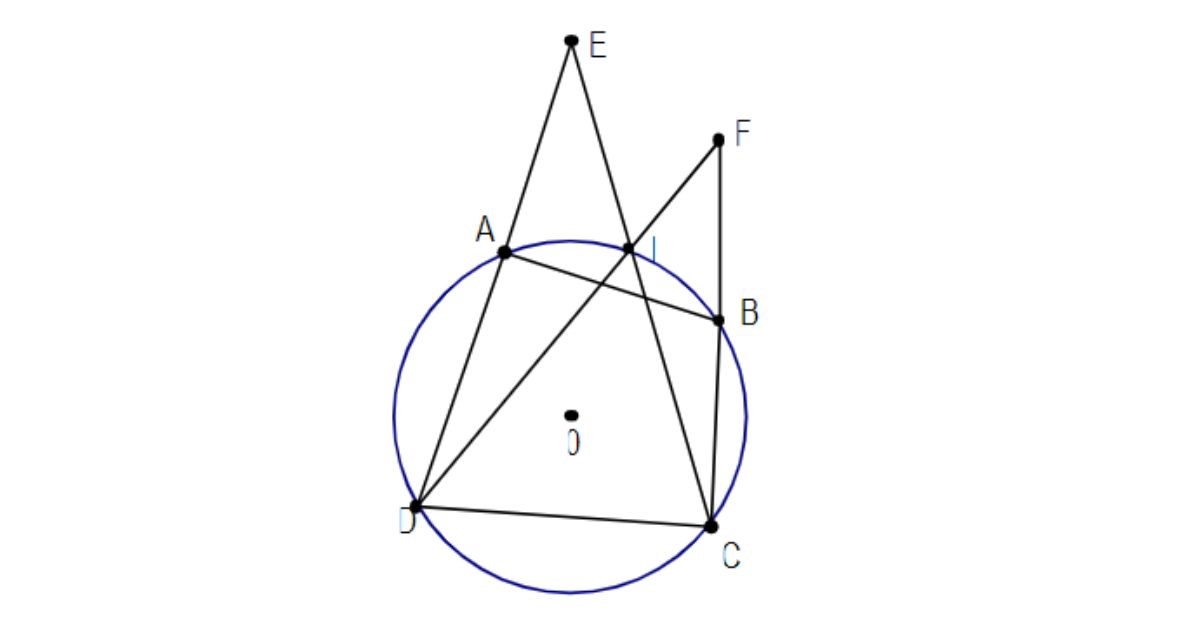
Hướng dẫn giải:
Để chứng minh được rằng tứ giác CDEF nội tiếp, ta có thể chứng minh 2 đỉnh không thuộc cạnh đó cùng nhìn cạnh đã chọn dưới 2 góc bằng nhau.
Chẳng hạn ta chọn cạnh DC, hãy tìm ra hai đỉnh E và F cùng nhìn DC dưới hai góc bằng nhau. Trong bài toán này ta chọn cạnh EF và chứng minh góc EDF bằng góc ECF bằng nửa số đo cung AI bằng nửa số đo cung BI.
Bài 2: Cho hình vuông ABCD, dựng góc xAy bằng 45 độ sao cho tia Ax cắt BD tại P, cắt BC tại Q; Tia Ay cắt BD tại F, CD tại E.
Chứng minh rằng:
a. Tứ giác ABQF nội tiếp
b. Tứ giác APED nội tiếp
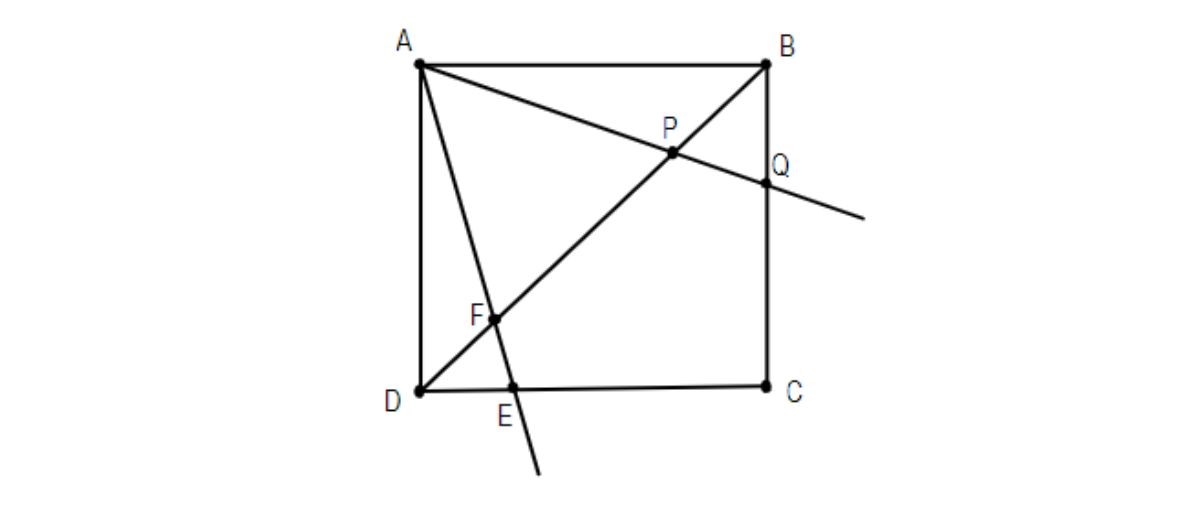
Hướng dẫn giải:
a. Hãy chỉ ra hai đỉnh A và B cùng nhìn đoạn QF dưới hai góc bằng 45 độ.
b. Hãy chỉ ra hai đỉnh A và D cùng nhìn đoạn EP dưới hai góc bằng 45 độ.
Bài 3: Cho đường tròn tâm O, M là một điểm nằm bên ngoài đường tròn. Từ M tạo hai tiếp tuyến MA và MB với đường tròn (A, B là hai tiếp điểm). Qua M vẽ cát tuyến MCD. Gọi I là trung điểm của CD.
a. Chứng minh tứ giác AIOB nội tiếp trong một đường tròn.
b. Gọi K là trung điểm của AM. Tia BK cắt đường tròn tại điểm thứ hai là P. Tia MP cắt đường tròn tại điểm thứ 2 là N. Chứng minh rằng AK2=KP.KB
c. Chứng minh rằng AM // BN
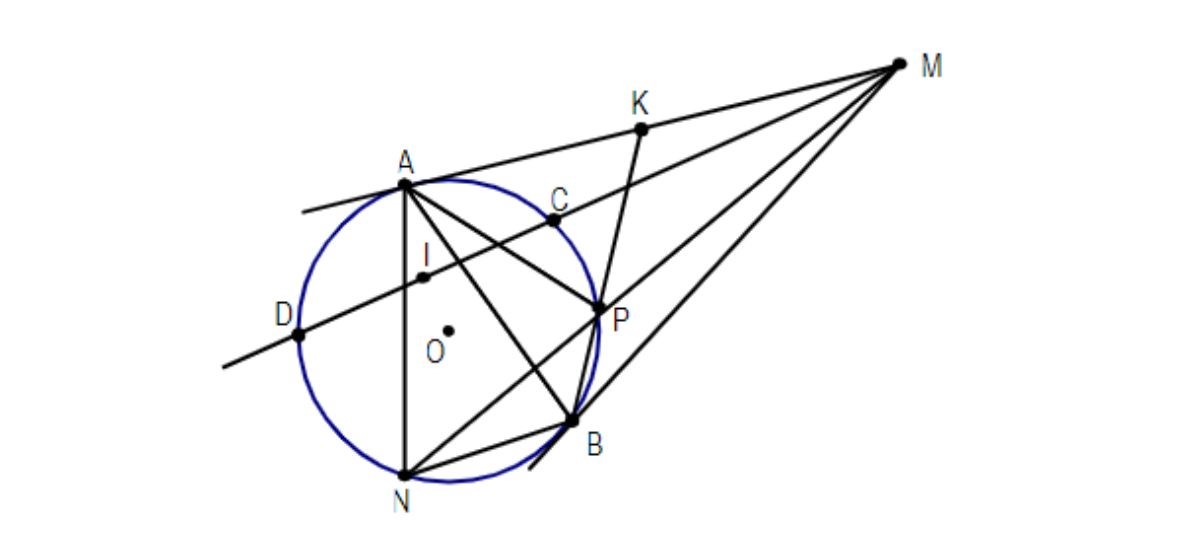
Hướng dẫn giải:
a. Chứng minh 5 đỉnh M, A, I, O, B cùng nhìn đoạn OM dưới một góc vuông. Từ đó suy ra tứ giác AIOB nội tiếp.
b. Chứng minh hai tam giác đồng dạng: tam giác AKB và tam giác PKA.
c. Chứng minh hai góc MNB và KMN bằng nhau. Tam giác AKB và tam giác PKA đồng dạng, suy ra hai tam giác BKM và MKP đồng dạng.
Bài 4: Cho tam giác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là hai tứ giác nội tiếp đường tròn.
Hướng dẫn giải:
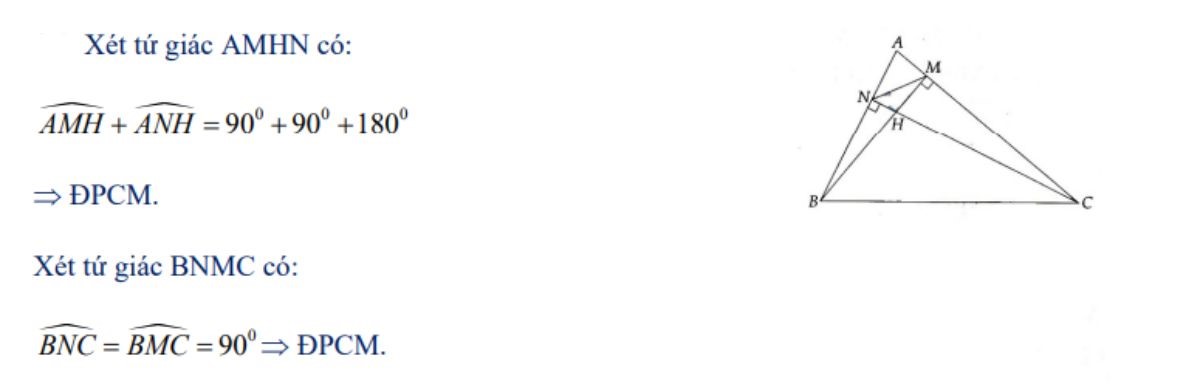
Bài 5: Cho đường tròn tâm O đường kính AB, gọi I là trung điểm của OA, dây CD vuông góc với AB tại I. Lấy K tùy ý trên cung BC nhỏ, AK cắt CD tại H.
a. Chứng minh BIHK là tứ giác nội tiếp đường tròn
b. Không phụ thuộc vào vị trí điểm K, hãy chứng minh AH.AK có giá trị
c. Kẻ DN và AC lần lượt vuông góc cạnh CB và DM. Chứng minh MN, AB, CD là các đường thẳng đồng quy.
Hướng dẫn giải:

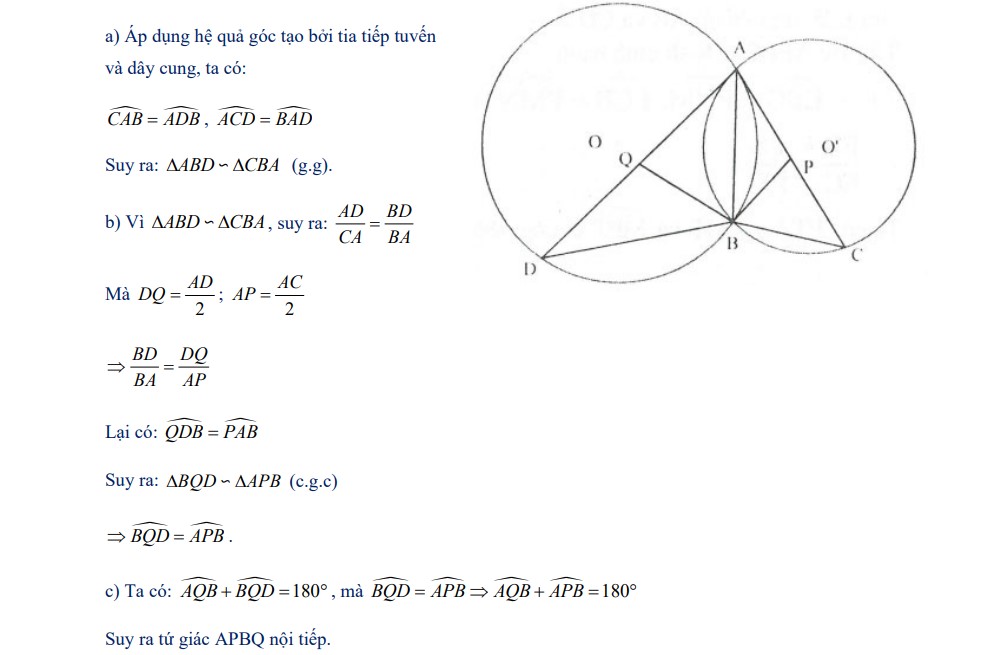
Bài 6: Cho hai đường tròn (O) và (O’) cắt nhau tại 2 điểm A và B. Các tiếp tuyến tại A của đường tròn (O) và (O’) cắt đường tròn (O’) và (O) lần lượt tại C và D. Gọi P là trung điểm của AC, Q là trung điểm của AD. Chứng minh rằng:
a. Hai tam giác ABD và CBD đồng dạng
b. Góc BQD và góc APB bằng nhau
c. Tứ giác APBQ nội tiếp
Hướng dẫn giải:
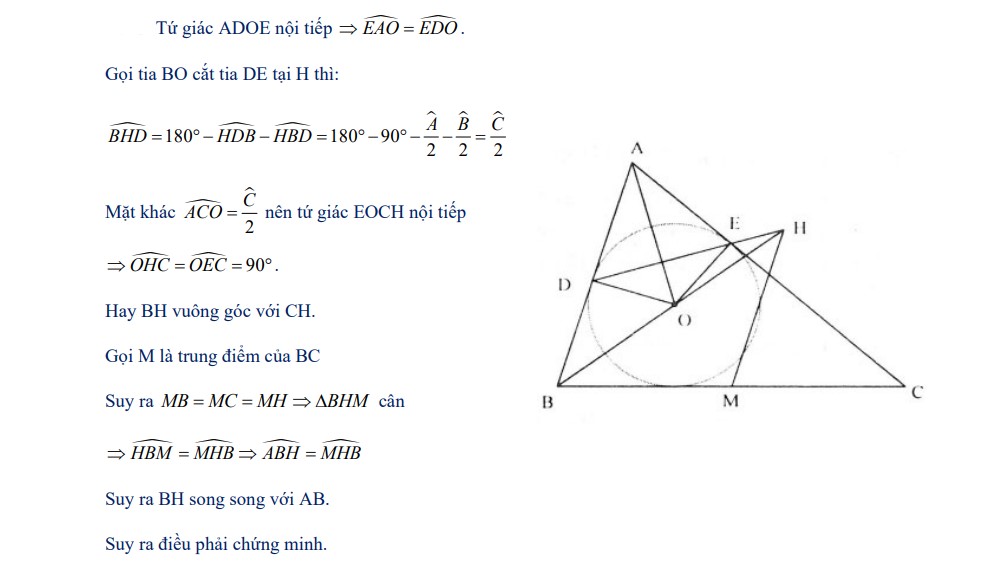
Bài 7: Cho tam giác ABC, D và E là các tiếp điểm của đường tròn nội tiếp với các cạnh AB và AC. Chứng minh đường phân giác trong của góc B, đường trung bình của tam giác song song với cạnh AB và đường thẳng DE là ba đường thẳng đồng quy.
Hướng dẫn giải:
Bài 8: Cho hai đường tròn (O;R) và (O’;R’) cắt nhau tại hai điểm phân biệt A và B. Từ điểm C thay đổi trên tia đối của tia AB, vẽ các tiếp tuyến CD, CE với đường tròn tâm O (D và E là các tiếp điểm) sao cho E nằm trong đường tròn tâm O’. AD cắt (O’) tại M, AE cắt (O’) tại N. Đường thẳng DE cắt MN tại I. Chứng minh rằng:
a. MI.BE = BI.AE
b. DE luôn đi qua một điểm cố định dù điểm C có thay đổi.
Hướng dẫn giải:

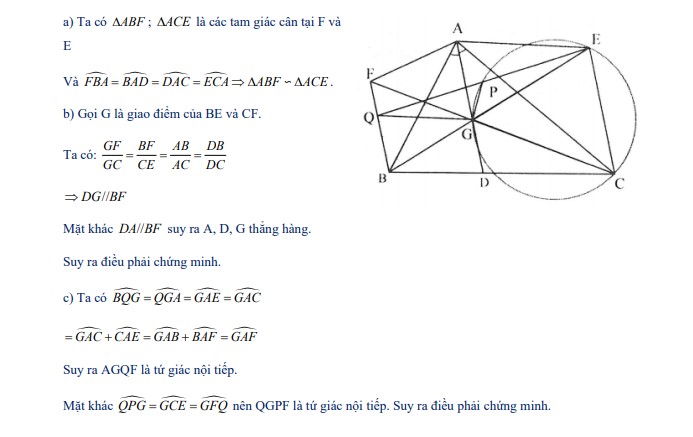
Bài 9: Cho tam giác ABC nhọn với AB < AC có AD là đường phân giác. Đường thẳng qua C song song với AD cắt đường trung trực của AC tại E. Đường thẳng qua B song song với AD cắt đường trung trực của AB tại F.
a. Chứng minh tam giác ABF đồng dạng với tam giác ACE.
b. Chứng minh rằng BE, CF, AD là các đường thẳng đồng quy, gọi điểm đó là G.
c. Từ G kẻ đường thẳng song song với AE cắt đường thẳng BF tại Q. Đường thẳng QE cắt đường tròn ngoại tiếp tam giác GEC tại P. Hãy chứng minh A, P, G, F, Q là các điểm cùng nằm trên một đường tròn.
Hướng dẫn giải:
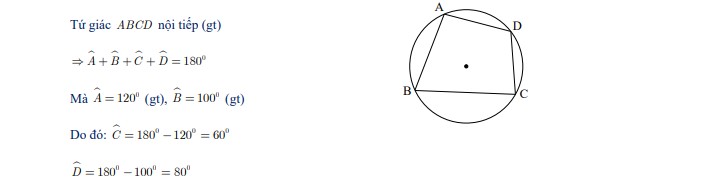
Bài 10: Cho tứ giác ABCD nội tiếp đường tròn tâm O có góc BAD bằng 120 độ, góc ABC bằng 100 độ. Tính góc BCD và góc CDA.
Hướng dẫn giải:
Bài 11: Cho tam giác ABC, từ A kẻ đường cao giao AB lại H. Gọi H1, H2 là điểm đối xứng của H lần lượt qua AB và AC. Đường thẳng H1H2 cắt AB và AC lần lượt tại K và I. Hãy chứng minh AH, BI và CK đồng quy.
Hướng dẫn giải:

Tham khảo bài viết cũ:
Trên đây là chuỗi bài tập chứng minh tứ giác nội tiếp. Đọc đề bài có thể cảm thấy khó nhưng khi biết cách vận dụng các công thức thì lại thật đơn giản phải không nào các em học sinh. Các em hãy chăm chỉ tìm thêm nhiều bài tập cùng chủ đề tứ giác nội tiếp để luyện tập thêm nhé!





















