Trong chương trình học toán lớp 9, bài tập chứng minh tam giác nội tiếp đường tròn hay bài tập chứng minh đường tròn ngoại tiếp tam giác là bài ăn điểm trong những đề kiểm tra. Các em học sinh chỉ cần nắm chắc lý thuyết, đọc kỹ đề bài là có thể giải quyết bài toán một cách dễ dàng. Dưới đây sẽ là những kiến thức về tam giác nội tiếp đường tròn và bài tập vận dụng liên quan mà HOCMAI muốn đưa tới các em.
I. Lý thuyết về tam giác nội tiếp đường tròn
1. Khái niệm
Một tam giác có 3 đỉnh nằm trên một đường tròn được gọi là tam giác nội tiếp đường tròn (hay đường tròn đó là đường tròn ngoại tiếp tam giác)
Ví dụ:

Cho tam giác ABC, có 3 đỉnh A, B, C cùng nằm trên một đường tròn tâm I
Vậy tam giác ABC là tam giác nội tiếp đường tròn tâm I
Hoặc đường tròn tâm I là đường tròn ngoại tiếp tam giác ABC
2. Định lý
Bất kỳ một tam giác nào cũng có một đường tròn ngoại tiếp.
3.Xác định tâm của đường tròn ngoại tiếp tam giác
- Tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh trong tam giác.
- Trong tam giác vuông, trung điểm cạnh huyền chính là tâm của đường tròn ngoại tiếp tam giác vuông ấy.
- Trong tam giác đều, tâm đường tròn ngoại tiếp và nội tiếp tam giác trùng với nhau.
II. Bài tập chứng minh tam giác nội tiếp đường tròn
Bài 1: Cho tam giác ABC ngoại tiếp đường tròn tâm O, khi đó ta có các đường trung trực OD, OE, OF lần lượt vuông góc tại tủng điểm của các cạnh AB, AC và BC như hình bên dưới:
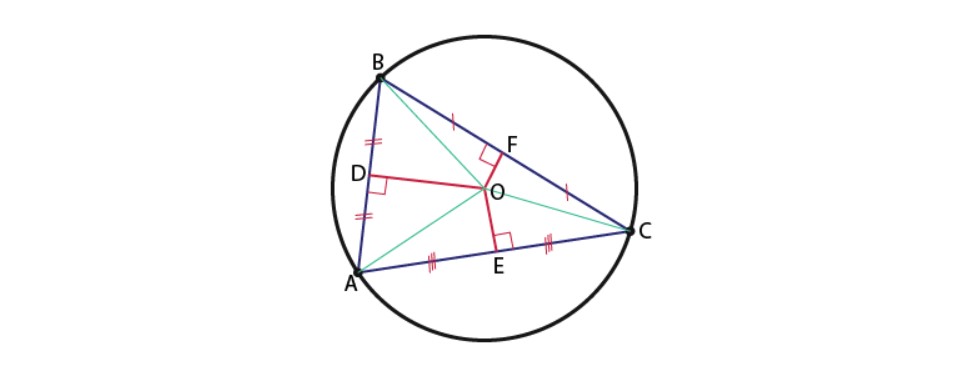
Hướng dẫn giải:
Nhìn hình vẽ ta thấy: các đường phân giác tương ứng là OB, OA và OC.
Xét tam giác OAB, ta có:
OD là đường trung trực tại cạnh AB, AD = DB
Tam giác ODA = tam giác ODB
OA = OB (1)
Xét tam giác OAC, ta có:
OE là đường trung trực tại cạnh AC, AE = EC
tam giác OEA = tam giác OEC
OA = OC (2)
Gọi r là bán kính đường tròn ngoại tiếp tâm O
Tứ (1) và (2) suy ra: r = OB = OA = OC (3)
Tiếp theo ta cần chứng minh khoảng cách từ O đến các cạnh tam giác ABC nhỏ hơn bán kính r.
Gọi điểm M bất kỳ nằm trên cạnh AD, ta có:
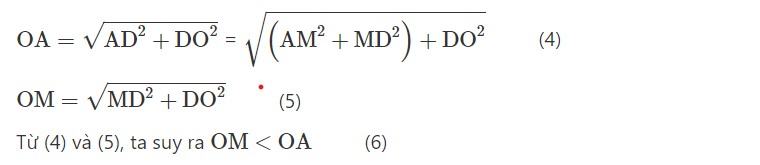
Từ đó suy ra khoảng cách từ tâm O đến các cạnh của tam giác ABC nhỏ hơn bán kính r của đường tròn.
Từ (3) và (6), ta có đường tròn tâm O là đường tròn ngoại tiếp tam giác ABC (điều cần chứng minh)
Bài 2: Hãy chứng minh:
a. Tâm của đường tròn ngoại tiếp tam giác là trung điểm của cạnh huyền thì tam giác đó là tam giác vuông.
b. Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Hướng dẫn giải:
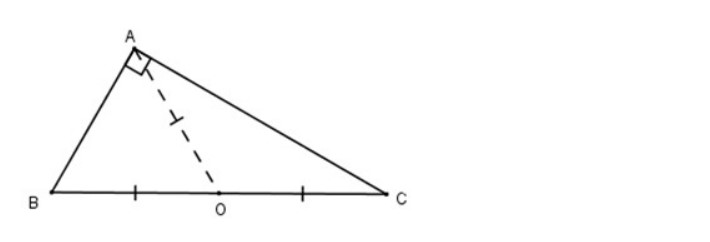


b. Xét tam giác ABC nội tiếp đường tròn tâm O đường kính BC.
Ta có: OA = OB = OC = r
Suy ra OA = 1/2 BC
do đó tam giác ABC vuông tại A (dựa theo tính chất đường trung tuyến trong tam giác vuông)
Bài 3: Nối ô ở cột trái với ô ở cột phải sao cho thích hợp:
|
(4) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên ngoài tam giác. |
|
(5) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên trong tam giác. |
|
(6) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh lớn nhất. |
| (7) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh nhỏ nhất. |
Hướng dẫn giải: (1) – (5), (2) – (6), (3) – (4).
Bài 4: Cho tam giác ABC nội tiếp đường tròn tâm C, tia phân giác của góc BAC cắt đường tròn tại M. Tạo đường cao AH. Hãy chứng minh:
a. M là trung điểm của dây BC
b. AM là tia phân giác của góc OAH.
Hướng dẫn giải:
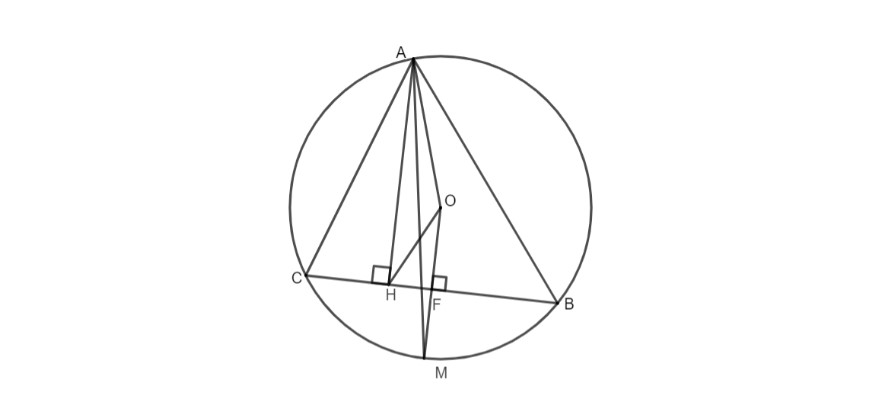

Kiến thức cơ bản liên quan:
Trên đây là kiến thức căn bản và những bài tập chứng minh tam giác nội tiếp. Để nắm rõ kiến thức hơn, các em học sinh hãy tìm thật nhiều bài tập khác để ôn luyện nhé. Cảm ơn các em đã đọc bài viết này và đừng quên truy cập vào hoctot.hocmai.vn để có thêm cho mình nhiều kiến thức bổ ích nữa nhé.

















