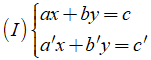BÀI 1. KHÁI NIỆM PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN.
I. PHƯƠNG TRÌNH HAI ẨN
Phương trình bậc nhất hai ẩn x, y là hệ thức có dạng: ax + by = c, trong đó a, b, c là các số đã biết (trong đó a ≠ 0 hoặc b ≠ 0 ).
* Trong phương trình ax + by = c, nếu giá trị của vế trái tại x = x0 và y =y0 bằng vế phải thì cặp số (x0; y0) được gọi là một nghiệm của phương trình.
Chú ý: Trong mặt phẳng tọa độ Oxy mỗi nghiệm của phương trình ax + by = c được biểu diễn bởi một điểm. Nghiệm (x0; y0) được biểu diễn bởi điểm có tọa độ (x0; y0).
II. HỆ PHƯƠNG TRÌNH HAI ẨN
Cho hai phương trình bậc nhất hai ẩn là ax + by = c và a’x + b’y = c’. Khi đó ta có hệ phương trình bậc nhất hai ẩn là:
Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP
+ Nếu hai phương trình có nghiệm chung là (x0; y0) thì (x0; y0) được gọi là một nghiệm của hệ phương trình (I).
+ Nếu hai phương trình không có nghiệm chung thì hệ phương trình (I) vô nghiệm.
+ Giải hệ phương trình là tìm tất cả các nghiệm của nó.
BÀI 2. GIẢI HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN.
+ Dạng 1. Giải hệ phương trình bậc nhất hai ẩn cơ bản.
+ Dạng 2. Hệ phương trình quy về hệ phương trình bậc nhất hai ẩn.
+ Dạng 3. Giải hệ phương trình bằng cách đặt ẩn phụ.
+ Dạng 4. Ứng dụng giải hệ phương trình trong bài toán tìm hệ số của hàm số.
+ Dạng 5. Ứng dụng giải hệ phương trình trong phản ứng hóa học.
BÀI 3. GIẢI BÀI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNH.
+ Dạng 1. Toán về quan hệ các số.
+ Dạng 2. Toán liên quan hình học.
+ Dạng 3. Toán chuyển động bộ.
+ Dạng 4. Toán chuyển động trên sông.
+ Dạng 5. Toán công việc.
+ Dạng 6. Toán về tỉ số phần trăm.
+ Dạng 7. Toán thực tế.
Tài liệu gồm 89 trang, được biên soạn bởi tác giả Trương Ngọc Vỹ, tổng hợp các dạng bài tập chuyên đề phương trình và hệ hai phương trình bậc nhất hai ẩn môn Toán 9 bộ sách Kết Nối Tri Thức Với Cuộc Sống (KNTTVCS), có đáp án và lời giải chi tiết.
Trên đây là tất cả các thông tin về nội dung Lý thuyết và bài tập phương trình bậc nhất hai ẩn, hệ phương trình bậc nhất hai ẩn. Hy vọng sẽ giúp em nắm kiến thức, định hướng học tập để phát triển tốt nhất. Các em hãy đừng quên truy cập hoctot.hocmai.vn để tham khảo thêm thật nhiều bài học bổ ích, những loại câu quan trọng nữa nhé!
Bài viết tham khảo thêm:
Lý thuyết và bài tập bất đẳng thức, bất phương trình bậc nhất một ẩn