Cách giải bất phương trình – Đầy đủ Lý thuyết và Bài tập

Ở cấp Trung học Cơ sở, các em học sinh khối 8 được cho là học nặng nhất bởi các em phải tiếp xúc với rất nhiều dạng toán mới như hằng đẳng thức ở đại số, các dạng hình học, tính chất và định lý của chúng. Tất cả là để chuẩn bị cho lớp 9 và kỳ thi lên cấp Trung học Phổ thông đầy cam go. Trong số những kiến thức các em được học thì kiến thức về bất phương trình rất nên được các em chú trọng. Bài viết dưới đây là cách giải bất phương trình với đầy đủ lý thuyết cần thiết và bài tập để các em ôn luyện.

A. LÝ THUYẾT BẤT PHƯƠNG TRÌNH

1. Bất phương trình một ẩn

– bất phương trình một ẩn là kiểu bất phương trình có dạng f(x) > g(x) ( hoặc f(x) < g(x); f(x) ≥ g(x); f(x) ≤ g(x)), trong đó f(x) và g(x) được gọi là hai biểu thức của  biến x.

– Cho số x0 được gọi là nghiệm của bất phương trình f(x) < g(x). Nếu thay x0 vào bất phương trình thì ta được f(x0) < g(x0) là một khẳng định đúng. Khi giải bất phương trình ta tìm được tất cả các nghiệm hay còn gọi là tập nghiệm của bất phương trình đó.

– Hai bất phương trình khi có chung tập nghiệm thì được gọi là hai bất phương trình tương đương nhau.

– Phép biến đổi tương đương xảy ra khi biến một bất phương trình thành một bất phương trình tương đương.

Một số quy tắc biến đổi phương trình tương đương thường dùng tới là:

– Chuyển vế : f(x) + h(x) > g(x) ⇔ f(x) > g(x) – h(x)

– Nhân (chia ) :

+ f(x) > g(x) ⇔ f(x) .h(x) > g(x).h(x) nếu h(x) > 0 với mọi x

+ f(x) > g(x) ⇔ f(x) .h(x) < g(x).h(x) nếu h(x) < 0 với mọi x

2. Bất phương trình bậc nhất một ẩn:

– Bất phương trình một ẩn là kiểu bất phương trình mà có dạng là ax + b > 0 ( hoặc ax + b < 0; ax + b ≥ 0; ax + b ≤ 0) trong đó số a, số b là các số cho trước và a ≠ 0.

– Giải bất phương trình ax + b > 0 (1)

Ta có (1) ⇔ ax > -b

+ Nếu a > 0 thì (1) ⇔ x > -b/a.

3. Bất phương bậc hai một ẩn:

– Phương trình bậc hai một ẩn có dạng: ax² + bx + c < 0 (hoặc  ax² + bx + c > 0,  ax² + bx + c ≤ 0,  ax² + bx + c ≥ 0)

Trong đó, x được gọi là ẩn; a, b, c là những số thực với a ≠ 0.

– Giải bất phương trình bậc hai ax² + bx + c < 0 thực chất là tìm các khoảng mà trong đó f(x) = ax² + bx + c < 0 cùng dấu với hệ số a (trong trường hợp a < 0) hoặc trái dấu với hệ số a (trong trường hợp a > 0)

Ví dụ 1: Giải bất phương trình sau: 3x² + 2x + 5 > 0

Đặt f(x) = 3x² + 2x + 5, ta có f(x) > 0 và a = 3 > 0, vậy nên f(x) luôn dương

Do đó tập nghiệm của bất phương trình là S = (-∞, +∞)

Ví dụ 2: f(x) = -2x² + 3x + 5, ta có a = -2 < 0 và f(x) = 0 ⇔ x = -1 hoặc x = 5/2

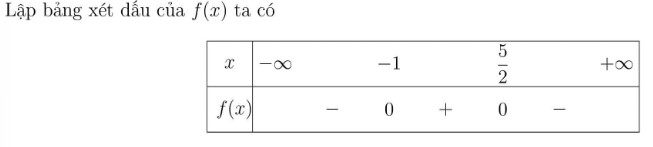
Dựa vào bảng xét dấu ta có tập nghiệm của bất phương trình là: S = (-1;5/2)

4. Tập nghiệm của bất phương trình:

– Số x = 0 gọi là nghiệm của một bất phương trình nào đó nếu ta thay x = 0 vào bất phương trình và kết quả ta được là một bất đẳng thức đúng.

+ Tập nghiệm của bất phương trình là tập hợp tất cả các nghiệm của bất phương trình đó. Khi ta có đề bài là giải bất phương trình thì có nghĩa là tìm tập nghiệm của bất phương trình đó.

+Hai bất phương trình được cho là tương đương nhau khi hai bất phương trình có cùng tập nghiệm.

Ví dụ:

+ Hình 1a biểu diễn tập nghiệm của bất phương trình x > 2

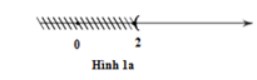
+ Hình 1b biểu diễn tập nghiệm của bất phương trình x ≤ 4

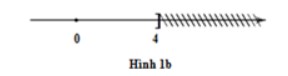
5. Những quy tắc cần nhớ

Quy tắc chuyển vế: Khi chuyển vế một hạng tử trong một bất phương trình từ vế bên này sang vế bên kia thì ta phải đổi dấu hạng tử đó.

Quy tắc nhân với một số:

Khi nhân hai vế của một bất phương trình với cùng một số khác số không,  ta phải:

+ Nếu số đó là số dương thì ta giữ nguyên chiều của bất phương trình.

+ Nếu số đó là số âm thì ta phải đổi chiều của bất phương trình.

6. Các dạng toán và phương pháp giải bất phương trình

Dạng 1: Xác định nghiệm hoặc tập nghiệm của một bất phương trình và biểu diễn nghiệm hoặc tập nghiệm đó trên trục số:

Phương pháp:

Ta sử dụng các quy tắc sau:

* Quy tắc chuyển vế: Khi chuyển vế một hạng tử trong một bất phương trình từ vế bên này sang vế bên kia thì ta phải đổi dấu hạng tử đó.

* Quy tắc nhân với một số: Khi nhân hai vế của một bất phương trình với cùng một số khác số không,  ta phải:

+ Nếu số đó là số dương thì ta giữ nguyên chiều của bất phương trình.

+ Nếu số đó là số âm thì ta phải đổi chiều của bất phương trình.

Ngoài ra, ta còn có thể sử dụng hằng đẳng thức hoặc quy đồng mẫu số để biến đổi bất phương trình.

Dạng 2: Xác định hai bất phương trình tương đương:

Phương pháp:

Bất phương trình tương đương: Hai bất phương trình được cho là tương đương nhau khi hai bất phương trình có cùng tập nghiệm.

Dạng 3: Giải bất phương trình bậc hai.

Phương pháp:

– Bước 1: Biến đổi bất phương trình về dạng một vế là tam thức bậc hai, một vế bằng 0

– Bước 2: Xét dấu vế trái của tam thức bậc hai và kết luận nghiệm.

Dạng 4: Giải bất phương trình tích.

Phương pháp:

– Bước 1: Biến đổi bất phương trình về dạng tích các nhị thức bậc nhất và tam thức bậc hai.

– Bước 2: Xét dấu các nhị thức bậc nhất và tam thức bậc hai ở trên và kết luận nghiệm.

Dạng 5: Giải bất phương trình chứa ẩn ở mẫu

Phương pháp:

– Bước 1: Biến đổi bất phương trình đã cho về dạng tích, thương các nhị thức bậc nhất và tam thức bậc hai.

– Bước 2: Xét dấu các nhị thức bậc nhất và tam thức bậc hai ở trên và kết luận nghiệm.

Chú ý: Cần chú ý điều kiện xác định của bất phương trình.

Dạng 6: Tìm điều kiện của tham số để bất phương trình vô nghiệm – có nghiệm – nghiệm đúng

Phương pháp:

– Sử dụng một số tính chất: Bình phương, căn bậc hai, giá trị tuyệt đối của một biểu thức luôn không âm.

Dạng 7: Giải hệ bất phương trình bậc hai

Phương pháp:

– Bước 1: Giải từng bất phương trình có trong hệ.

– Bước 2: Kết hợp nghiệm và kết luận.

B. BÀI TẬP BẤT PHƯƠNG TRÌNH

I. TRẮC NGHIỆM VỀ BẤT PHƯƠNG TRÌNH

Câu 1: Bất phương trình ax + b > 0 vô nghiệm khi:

A) a ≠ 0 và b = 0

B) a > 0 và b = 0

C) a = 0 và b ≠ 0

D) a = 0 và b ≠ 0

Đáp án chính xác là: D

Câu 2: Tập nghiệm S của bất phương trình: 5x – 1 ≥ (2x/5) + 3 là?

A) S = R

B) x > 2

C) x < (-5)/2

D) x ≥ 20/23

Đáp án chính xác là: D

Câu 3: Bất phương trình [(3x + 5)/2] -1 ≤ [(x + 2)/3 + x] có bao nhiêu nghiệm là nghiệm nguyên lớn hơn 10?

A) 4

B) 5

C) 9

D) 10

Đáp án chính xác là: B

Câu 4: Tập nghiệm S của bất phương trình: (1 – √2)x < √2 – 2 là?

A) x > 2

B) x > √2

C) x < -√2

D) S = R

Đáp án chính xác là: B

Câu 5: Bất phương trình (2x – 1)(x + 3) – 3x + 1 ≤ (x – 1)(x + 3) + x² – 5 có tập nghiệm là?

A) x < -2/3

B) x ≥ -2/3

C) S = R

D) S = Ø

Đáp án chính xác là: D

Câu 6: Giải bất phương trình: 2x + 4 < 16

A) x > 6

B) x < 6

C) x < 8

D) x > 8

Đáp án chính xác là: B

Câu 7: Giải bất phương trình: 8x + 4 > 2(x + 5)

A) x > 2

B) x < -1

C) x > -1

D) x > 1

Đáp án chính xác là: D

Câu 8: Giải bất phương trình: (x + 2)/3 +3x + 1 > (x – 2)/2

A) x > -6/7

B) x < 6/5

C) x > -16/17

D) x > -6/11

Đáp án chính xác là: C

Câu 9: Giải bất phương trình: (x + 2)(x – 3) > (2 – x)(6 – x)

A) x > 18/7

B) x > 11/7

C) x < 15/7

D) x < 8/7

Đáp án chính xác là: A

Câu 10: Tìm m để x = 2 là nghiệm của bất phương trình: mx + 2 < x + 3 + m

A) m = 2

B) m < 3

C) m > 1

D) m < -3

Đáp án chính xác là: B

Câu 11: Những bất phương trình nào là bất phương trình một ẩn?

A) 2x – 3 < 0

B) 0.x + 5 > 0

C) 5x – 15 ≥ 0

D) x² > 0

Đáp án chính xác là: A và C

II. TỰ LUẬN VỀ BẤT PHƯƠNG TRÌNH:

Bài 1: Giải các bất phương trình (theo quy tắc chuyển vế)

a) x – 3 > 5

b) 2x ≥ x + 2

c) 2x – 4 < 3x – 2

d) 2,5 – 2x ≤ -x – 3,5

e) 3x – 5 > 2(x – 1) + x

Hướng dẫn giải bài:

a) x – 3 > 5

⇔ x > 5 + 3

⇔ x > 8

Vậy tập nghiệm của bất phương trình là S = {x|x > 8}

b) 2x ≥ x + 2 

⇔ 2x – x ≥ 2

⇔ x ≥ 2

Vậy tập nghiệm của bất phương trình là: S = {x|x ≥ 2}

c) 2x – 4 < 3x – 2

⇔ 3x – 2x > -4 + 2

⇔ x > -2

Vậy tập nghiệm của bất phương trình là: S = {x|x > -2}

d) 2,5 – 2x ≤ -x – 3,5

⇔ 2,5 + 3,5 ≤ -x + 2x

⇔ x ≥ 6

Vậy tập nghiệm của bất phương trình là: S = {x|x ≥ 6}

e) 3x – 5 > 2(x – 1) + x

⇔ 3x – 5 > 2x – x + x

⇔ 3x – 3x > -2 + 5

⇔ 0x > 3

Vậy bất phương trình vô nghiệm

Bài 2: Giải các bất phương trình sau và biểu diễn tập nghiệm của mỗi bất phương trình trên một trục số:

a) 2x – 3 > 3(x – 2)

b) (12x + 1)/12 ≤ (9x + 1)/3 – (8x + 1)/4

c) 5(x – 1) ≤ 6(x – 5/3)

d) (2x – 1)/2 – (x + 1)/6 ≥ (4x – 5)/3

Hướng dẫn giải bài:

a) Ta có:

2x – 3 > 3(x – 2)

⇔ 2x – 3 > 3x – 6

⇔ 6 – 3 > 3x – 2x

⇔ x < 3

Vậy tập nghiệm của bất phương trình là: S = {x|x < 3}

+ Biểu diễn trục số:

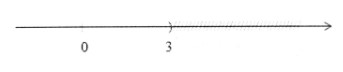
b) Ta có:

(12x + 1)/12 ≤ (9x + 1)/3 – (8x + 1)/4

⇔ (12x + 1)/12 ≤ [4(9x + 1) – 3(8x + 1)]/12

⇔ 12x + 1 ≤ 36x + 4 – 24x – 3

⇔ 12x + 1 ≤ 12x + 1 (luôn đúng với mọi giá trị x)

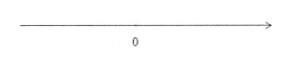
Vậy tập nghiệm của bất phương trình là S = R

+ Biểu diễn trên trục số:

c) ta có:

5(x – 1) ≤ 6(x – 5/3)

⇔ 5x – 5 ≤ 6x – 10

⇔ 10 – 5  ≤ 6x – 5x

⇔ x ≥ 5

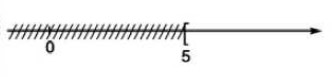
Vậy tập nghiệm của bất phương trình là: S = {x|x ≥ 5}

+ Biểu diễn trục số:

d) Ta có:

(2x – 1)/2 – (x + 1)/6 ≥ (4x – 5)/3

⇔ [3(2x – 1) – (x + 1)]/6 ≥ [2(4x – 5)]/6

⇔ 3(2x – 1) – (x + 1) ≥ 2(4x – 5)

⇔ 6x – 3 – x – 1 ≥ 8x – 10

⇔ 3x ≤ 6

⇔ x ≤ 2

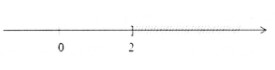
Vậy tập nghiệm của bất phương trình là: S = {x|x ≤ 2}

+ Biểu diễn trục số:

Bài 3: Giải các bất phương trình bậc hai một ẩn sau:

a) -3x² + 2x + 1 < 0

b) x² + x – 12 < 0

c) 5x² -6√5x + 9 > 0

d) -36x² + 12x -1 ≥ 0

Hướng dẫn giải bài:

Bài 4: Tìm m để mọi x ∈ [-1;1] đều là nghiệm của bất phương trình:

3x² – 2(m + 5)x – m² + 2m + 8 ≤ 0

Hướng dẫn giải bài:

Bài viết xem thêm:

Giải phương trình và bất phương trình chứa dấu giá trị tuyệt đối

Trên đây là cách giải bất phương trình mà HOCMAI muốn các em khối 8 tham khảo là luyện tập theo. Những lý thuyết bên trên rất cô đọng và được biên soạn sát sườn với sách giáo khoa của cá em vậy nên chúng rất thực tiễn và áp dụng được vào bài tập của các em ở trên lớp. Những bài tập trên tuy rất cơ bản nhưng các em chỉ cần luyện tập nhiều lần là có thể ghi nhớ được kiến thức bất phương trình này. Các em cũng đừng quên truy cập vào website hoctot.hocmai.vn để tìm thêm cho mình nhiều bài học bổ ích nữa nhé!