Công thức nghiệm thu gọn của phương trình bậc 2 – Toán lớp 9

A. Lý thuyết về công thức nghiệm thu gọn 

1. Nhắc lại kiến thức công thức nghiệm

Đối với phương trình có dạng ax² + bx + c = 0 (a ≠ 0)

Ta có biệt thức của phương trình là: Δ = b² – 4ac

• Trường hợp 1: Nếu Δ > 0 thì ta có phương trình có 2 nghiệm phân biệt

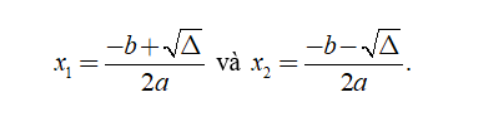
• Trường hợp 2: Nếu Δ = 0 thì ta có phương trình có nghiệm kép

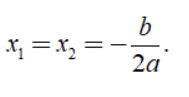
• Trường hợp 3:  Nếu Δ < 0 thì ta có phương trình đã cho vô nghiệm

Chi tiết về kiến thức và các dạng bài về công thức nghiệm xem tại: Công thức nghiệm của phương trình bậc 2

2. Công thức nghiệm rút gọn

Đối với phương trình ax² + bx + c = 0 (a ≠ 0) và b = 2b’; Δ’ = b’² – ac.

• Trường hợp 1: Δ’ > 0, phương trình có hai nghiệm phân biệt

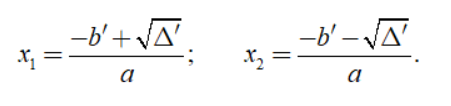
• Trường hợp 2: Δ’ = 0, phương trình có 1 nghiệm duy nhất (hoặc 2 nghiệm trùng nhau)

x₁ = x₂ = -b’/a

• Trường hợp 3: Δ’ < 0, phương trình bậc 2 vô nghiệm

Lưu ý:

• Khi a > 0 mà phương trình ax² + bx + c = 0 là phương trình vô nghiệm thì ax² + bx + c > 0 với mọi x
• Đối với phương trình bậc 2 khuyết thiếu có dạng ax² + bx = 0 hoặc ax² + c = 0 các em học sinh tiến hành giải trực tiếp không qua biệt số sẽ nhanh và dễ giải hơn

B. Các dạng bài thương gặp về công thức nghiệm phương trình bậc 2 thu gọn

Dạng bài tập 1: Giải phương trình bậc 2 một ẩn bằng phương pháp dùng công thức nghiệm thu gọn

Xét phương trình bậc 2 một ẩn có dạng ax² + bx + c = 0 (a ≠ 0) và b = 2b’; Δ’ = b’² – ac.

• Nếu Δ’ > 0, phương trình có hai nghiệm phân biệt

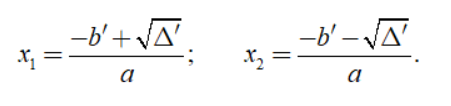
• Nếu Δ’ = 0, phương trình có 1 nghiệm duy nhất x₁ = x₂ = -b’/a

• Trường hợp 3: Δ’ < 0, phương trình bậc 2 vô nghiệm

Dạng bài tập 2: Khảo sát số nghiệm của hàm số bậc 2

Xét phương trình bậc 2 một ẩn có dạng ax² + bx + c = 0 (a ≠ 0) và b = 2b’

• Phương trình có nghiệm kép khi:
  a ≠ 0
  Δ’ = 0
• Phương trình có 2 nghiệm:
  a ≠ 0
  Δ’ > 0
• Phương trình vô nghiệm khi:
  Δ’ < 0 hoặc a = 0; b = 0 và c ≠ 0

Dạng bài tập 3: Biện luận số nghiệm của phương trình theo ẩn m

Đây là dạng bài có biến số m thay đổi và các em học sinh phải tìm điều kiện để thỏa mãn các điều kiện như: phương trình có 2 nghiệm, phương trình có 1 nghiệm duy nhất hay phương trình vô nghiệm.

Xét phương trình bậc 2 một ẩn có dạng ax² + bx + c = 0 (a ≠ 0) và Δ = b² – 4ac (hoặc có  b = 2b’; Δ’ = b’² – ac)

• Nếu Δ > 0 (hoặc Δ’ > 0), phương trình có hai nghiệm phân biệt
• Nếu Δ = 0 (hoặc Δ’ = 0), phương trình có 1 nghiệm duy nhất
• Nếu Δ < 0 (hoặc Δ’ < 0), phương trình bậc 2 vô nghiệm

C. Một số bài tập thực hành

Bài tập cơ bản

Bài tập chứa tham số

Hướng dẫn giải

Hướng dẫn giải

Hướng dẫn giải

 Trên đây là toàn bộ kiến thức về công thức nghiệm thu gọn. Hy vọng bài viết sẽ giúp các em học sinh có thêm kiến thức phục vụ cho quá trình giải bài tập Toán lớp 9 cũng như là cuốn sổ tay trong quá trình ôn thi Toán vào 10.