Đề cương ôn thi học kì 2 toán 7 (Có đề thi + hướng dẫn giải)

Đề cương ôn thi học kì 2 Toán 7 là tài liệu ôn thi hay, giúp học sinh hệ thống toàn bộ kiến thức đã được học trong học kì 2 Toán lớp 7. Tài liệu bao gồm các dạng Toán trọng tâm, bài tập ôn luyện cùng đề tham khảo (có đáp án) giúp các bạn ôn tập lại lý thuyết và luyện tập các dạng bài khác nhau để chuẩn bị tốt nhất cho bài thi học kì 2 sắp tới. 

Bài viết tham khảo thêm:

• Đề cương ôn thi học kì 2 tiếng anh 7
• Đề cương ôn thi học kì 2 Văn 7

 

A. Lý thuyết ôn thi học kì 2 toán 7

I – Phần đại số – Toán 7

Trong phần đại số học kỳ II toán lớp 7, các em cần ôn tập kĩ một số kiến thức sau:

1) Dấu hiệu điều tra, tần số, mốt và Công thức tính số trung bình cộng của dấu hiệu.

– Dấu hiệu điều tra, tần số, mốt của dấu hiệu:

• Dấu hiệu điều tra là vấn đề hoặc hiện tượng mà người điều tra quan tâm, tìm hiểu.
• Tần số của giá trị là số lần một giá trị xuất hiện trong dãy các giá trị của dấu hiệu.
• Mốt của dấu hiệu là giá trị có tần số lớn nhất ở trong bảng ”tần số”. Ký hiệu là Mo.

– Công thức tính số TBC (Trung bình cộng):

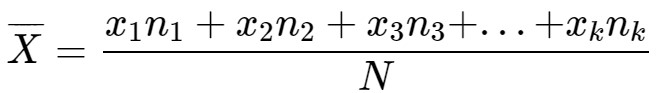
2) Vẽ biểu đồ đoạn thẳng (dạng cột, hình chữ nhật)

a) Cách dựng biểu đồ đoạn thẳng:

• Dựng hệ trục tọa độ: Trục hoành biểu diễn các giá trị x và trục tung biểu diễn tần số n (độ dài đơn vị ở trên hai trục có thể khác nhau).
• Xác định các điểm có tọa độ là cặp số bao gồm giá trị và tần số của nó (giá trị viết trước còn tần số viết sau).
• Nối mỗi điểm đó cùng với điểm trên trục hoành có cùng hoành độ.

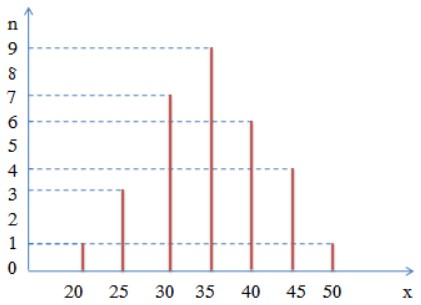
b) Cách dựng biểu đồ hình chữ nhật:

Cách dựng như biểu đồ đoạn thẳng, các đoạn thẳng trong biểu đồ đoạn thẳng được thay bằng hình chữ nhật.

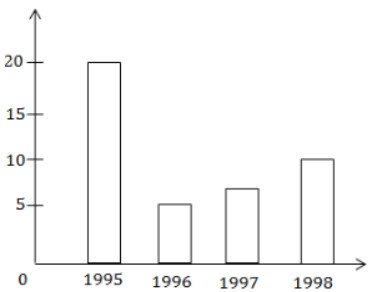
3) Biểu thức đại số, Giá trị biểu thức đại số

a) Biểu thức đại số là những biểu thức bao gồm các phép tính toán cộng, trừ, nhân, chia, nâng lên lũy thừa không chỉ trên những số mà còn có thể ở trên những chữ (đại diện cho các số).

Vd: 2x-5,…

Trong một biểu thức đại số:

• Biến số là những chữ đại diện cho một số tùy ý 
• Hằng số là những chữ đại diện cho một số xác định

b) Tính giá trị của một biểu thức đại số theo các bước sau:

• Bước 1: Thay chữ bởi các giá trị số đã cho (chú ý đến các trường hợp phải đặt số ở trong dấu ngoặc).
• Bước 2: Thực hiện các phép tính (chú ý tới thứ tự thực hiện các phép tính: thực hiện các phép lũy thừa, rồi đến phép nhân chia và sau đó là phép cộng trừ).

4) Đơn thức

a) Đơn thức là biểu thức đại số gồm chỉ một số, hoặc một biến, hoặc là một tích giữa các số và các biến. Số 0 gọi là đơn thức không.

b) Bậc của đơn thức: Với một đơn thức bất kỳ (≠0) thì bậc của đơn thức chính là tổng của số mũ của tất cả các biến chứa ở trong đơn thức đó. Mọi số thực (≠0) luôn có bậc bằng 0 và số 0 được xem là một đơn thức không có bậc.

c) Hai đơn thức đồng dạng là hai đơn thức có hệ số ≠ 0 và có cùng phần biến. Các số ≠ 0 được coi là những đơn thức đồng dạng. Chú ý: Mọi số ≠ 0 được coi là các đơn thức đồng dạng với nhau. 

d) Tính cộng trừ đơn thức đồng dạng: Để cộng (hoặc trừ) các đơn thức đồng dạng, ta cộng (hoặc trừ) các hệ số cùng với nhau và giữ nguyên phần biến.

5) Đa thức

a) Đa thức là biểu thức bao gồm các biến và các hệ số, chỉ sử dụng các phép cộng, phép trừ, phép nhân, và lũy thừa cùng với số mũ tự nhiên của các biến.

b) Bậc của đa thức là bậc của hạng tử có bậc cao nhất ở trong dạng thu gọn của đa thức đó.

c) Thu gọn đa thức:

– Nếu trong đa thức có chứa những đơn thức đồng dạng thì ta cần thu gọn các đơn thức đồng dạng đó để thu được một đa thức thu gọn.

– Đa thức được gọi là đã thu gọn nếu như trong đa thức không còn 2 hạng tử nào đồng dạng.

→ Cách thu gọn đa thức: Ta cần gom nhóm các hạng tử đồng hạng và thực hiện các phép cộng những hạng tử đồng hạng này.

6) Đa thức một biến

a) Đa thức 1 biến là tổng của những đơn thức của cùng một biến. Một số được gọi là một đa thức một biến. Bậc của đa thức một biến (khác đa thức không, đã được thu gọn) là số mũ lớn nhất của biến ở trong đa thức đó. 

b) Sắp xếp đa thức 1 biến: Để thuận lợi cho việc tính toán đối với những đa thức một biến, người ta thường sắp xếp các hạng tử của chúng theo lũy thừa tăng hoặc giảm của biến.

Mọi đa thức bậc 2 của biến x, sau khi ta sắp xếp các hạng tử của chúng theo lũy thừa giảm của biến, đều sẽ có dạng: ax2 + bx + c. Trong đó a,b và c là các số cho trước và a ≠ 0.

Chú ý:

• Để sắp xếp các hạng tử của 1 đa thức, trước hết cần phải thu gọn đa thức đó.
• Các chữ đại diện cho những số xác định cho trước được gọi là hằng số.

c) Tính tổng hiệu đa thức 1 biến

Để cộng (hoặc trừ) các đa thức một biến, ta có thể làm một trong hai cách sau:

• Cách 1: Cộng hoặc trừ đa thức theo “hàng ngang”
• Cách 2: Sắp xếp các hạng tử của cả 2 đa thức cùng theo lũy thừa giảm (hay tăng) của biến rồi đặt phép tính theo cột dọc tương ứng như cộng hoặc trừ các số (chú ý đặt các đơn thức đồng dạng cùng một cột).

d) Nghiệm của đa thức 1 biến: Nếu tại x=a, đa thức P(x) có giá trị = 0 ⇒ Ta nói a (hoặc x = a) là một nghiệm của đa thức đó.

Một nghiệm có thể có 1,2,3,n,… nghiệm hoặc không có nghiệm nào ⇒ Số nghiệm của một đa thức (khác đa thức ≠0) không vượt quá bậc của nó.

 

II – Phần Hình học – Toán 7

Trong phần toán hình học học kỳ II lớp 7, các em cần ôn tập kĩ một số kiến thức sau:

1) Các trường hợp bằng nhau của hai tam giác:

• Cạnh – cạnh – cạnh (c.c.c)
• Cạnh – góc – cạnh (c.g.c)
• Góc – cạnh – góc (g.c.g)

2) Tam giác cân

a) Tam giác cân là tam giác có 2 cạnh bằng nhau. 

b) Tính chất: Trong một  tam giác cân, hai góc đáy bằng nhau.

c) Dấu hiệu nhận biết:

• Nếu một tam giác có 2 cạnh bằng nhau ⇒ Tam giác đó là tam giác cân.
• Nếu một tam giác có 2 góc bằng nhau ⇒ Tam giác đó là tam giác cân.

3)Tam giác đều

a) Tam giác đều là tam giác có 3 cạnh bằng nhau.

b) Tính chất: Trong một tam giác đều, mỗi góc bằng 60°

c) Dấu hiệu nhận biết:

• Nếu tam giác có 3 cạnh bằng nhau ⇒ Tam giác đó là tam giác đều.
• Nếu tam giác có 3 góc bằng nhau ⇒ Tam giác đó là tam giác đều.
• Nếu một tam giác cân có 1 góc nhọn bằng 60° ⇒ Tam giác đó là tam giác đều.

4) Định lý Pitago

Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương của 2 cạnh góc vuông.

ΔABC vuông góc tại A ⇒ BC² = AB² + AC²

5) Quan hệ cạnh góc trong một tam giác:

Trong một tam giác:

• Góc đối diện cùng với cạnh lớn hơn là góc lớn hơn
• Cạnh đối diện cùng với góc lớn hơn là cạnh lớn hơn

6) Quan hệ giữa đường xiên và hình chiếu | đường vuông góc và đường xiên

Từ điểm A không nằm trên đường thẳng d, kẻ một đường thẳng vuông góc cùng với d tại H. Khi đó:

• Đoạn thẳng AH được gọi là đường vuông góc hay đoạn vuông góc kẻ từ điểm A tới đường thẳng d; điểm H gọi là chân của đường vuông góc hay hình chiếu của A trên đường thẳng d.
• Đoạn thẳng AB được gọi là một đường xiên kẻ từ điểm A tới đường thẳng d.
• Đoạn thẳng HB được gọi là hình chiếu của đường xiên AB ở trên đường thẳng d.

a) Quan hệ giữa Đường vuông góc & Đường xiên

Trong các Đường vuông góc & Đường xiên kẻ từ một điểm nằm ngoài một đường thẳng tới đường thẳng đó, đường vuông góc là đường thẳng ngắn nhất.

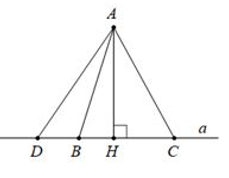
b) Các đường xiên & Hình chiếu của chúng

Trong hai đường xiên kẻ từ một điểm nằm bên ngoài một đường thẳng đến đường thẳng đó:

1. Đường xiên nào có hình chiếu lớn hơn ⇒ lớn hơn.

AH ⊥ a, HD > HC ⇒ AD > AC

2. Đường xiên nào lớn hơn ⇒ Có hình chiếu lớn hơn.

AH ⊥ a, AD > AC ⇒ HD > HC

3. Nếu hai đường xiên bằng nhau ⇒ Hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau ⇒ Hai đường xiên bằng nhau.

AB = AC ⇔ HB = HC

7) Bất đẳng thức trong tam giác

Định lý: Trong một tam giác, tổng độ dài của hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài của cạnh còn lại.

8) Tính chất 3 đường trung tuyến

Định lý: 

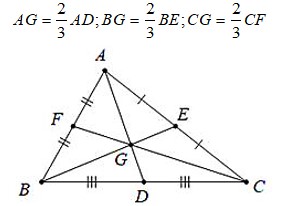
– Giao điểm của 3 đường trung tuyến của tam giác được gọi là trọng tâm.

– 3 đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.

Ví dụ: Với G là trọng tâm của tam giác ABC:

9) Tính chất phân giác của một góc

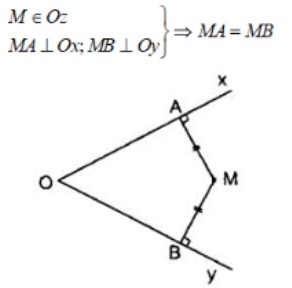
Tia phân giác của một góc chia góc đó trở thành 2 góc nhỏ có số đo bằng nhau và bằng một nửa (1/2) góc ban đầu. Tất cả các điểm nằm ở trên tia phân giác của một góc sẽ cách đều 2 tia tạo thành góc.

10) Tính chất 3 đường phân giác tròn tam giác

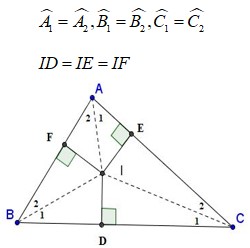
Trong tam giác cân, đường phân giác xuất phát từ đỉnh đối diện cùng với đáy đồng thời là đường trung tuyến ứng với cạnh đáy. Ba đường phân giác của một Δ cùng đi qua một điểm. Điểm này cách đều 3 cạnh của tam giác đó.

11) Tính chất 3 đường trung trực của tam giác

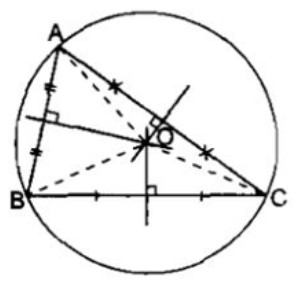
Trong tam giác, 3 đường trung trực đồng quy tại một điểm, điểm đó cách đều 3 đỉnh của Δ và là tâm của đường tròn ngoại tiếp tam giác ấy. 

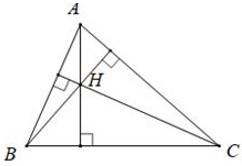
12) Tính chất 3 đường cao trong một tam giác

Ba đường cao của Δ cùng đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác.

Ví dụ: H là giao điểm của 3 đường cao của tam giác ABC. H là trực tâm của ΔABC

B. Bài tập ôn thi học kì 2 toán 7

I – Thống kê

Câu 1: Điểm kiểm tra môn toán học kỳ I của học sinh tại lớp 7A được ghi lại như sau:

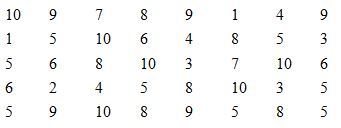
a) Dấu hiệu cần tìm là gì?

b) Hãy lập bảng tần số và tìm số trung bình cộng.

c) Tìm mốt của dấu hiệu.

d) Dựng biểu đồ đoạn thẳng (trục tung biểu diễn tần số, trục hoành biểu diễn điểm số).

Câu 2. Một giáo viên theo dõi thời gian làm bài tập (thời gian được tính theo phút) của 30 học sinh của một trường (ai cũng làm được).  Người ta lập bảng sau:

Thời gian (x)	5	7	8	9	10	14
Tần số (n)	4	3	8	8	4	3	N = 30

a) Dấu hiệu là gì? Tính mốt của dấu hiệu?

b) Tính thời gian trung bình của 30 học sinh khi làm bài tập?

c) Nhận xét về thời gian để làm bài tập của học sinh so với thời gian trung bình.

Câu 3. Số học sinh giỏi của các lớp khối 7 được ghi lại như sau:

Lớp	7A	7B	7C	7D	7E	7G	7H
Số HS giỏi	32	28	32	35	28	26	28

a) Dấu hiệu ở đây là gì? Đơn vị điều tra là gì?

b) Lập bảng tần số và cho nhận xét.

c) Vẽ biểu đồ đoạn thẳng.

Câu 4: Tổng số điểm của 4 môn thi của các học sinh trong một phòng thi được liệt kê trong bảng dưới đây.

32	30	22	30	30	22	31	35
35	19	28	22	30	39	32	30
30	30	31	28	35	30	22	28

a) Dấu hiệu ở đây là gì? Số tất cả các giá trị bằng bao nhiêu? số giá trị khác nhau của dấu hiệu?

b) Lập bảng tần số, cho nhận xét

c) Tính trung bình cộng của dấu hiệu và tìm mốt

Câu 5: Lớp 7A góp tiền ủng hộ đồng bào bị ảnh hưởng bởi thiên tai. Số tiền góp của mỗi bạn được thống kê trong bảng dưới đây (Đơn vị: Nghìn đồng)

1	2	1	4	2	5	2	3	4	1	5	2
3	5	2	2	4	1	3	3	2	4	2	3
4	2	3	10	5	3	2	1	5	3	2	2

a) Dấu hiệu ở đây là gì?

b) Lập bảng tần số và tìm trung bình cộng

Câu 6: Thời gian làm bài tập của các bạn học sinh lớp 7 tính bằng phút được thống kê dưới bảng sau:

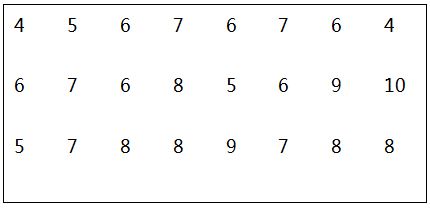
a) Dấu hiệu là gì? Số các giá trị bằng bao nhiêu?

b) Lập bảng tần số? Tìm mốt của dấu hiệu? Tìm số trung bình cộng?

c) Vẽ biểu đồ đoạn thẳng?

Câu 7: Số cơn bão hàng năm đổ bộ vào lãnh thổ của Việt Nam trong suốt 20 năm cuối cùng của thế kỷ XX được ghi lại ở trong bảng sau:

3	3	6	6	3	5	4	3	9	8
2	4	3	4	3	4	3	5	2	2

a) Dấu hiệu ở đây là gì?

b) Lập bảng tần số và tính xem trong thời gian 20 năm, mỗi năm trung bình có bao nhiêu cơn bão đã đổ bộ vào nước ta? Tìm mốt?

c) Biểu diễn bảng tần số nói trên bằng biểu đồ đoạn thẳng.

II – Đơn thức và đa thức

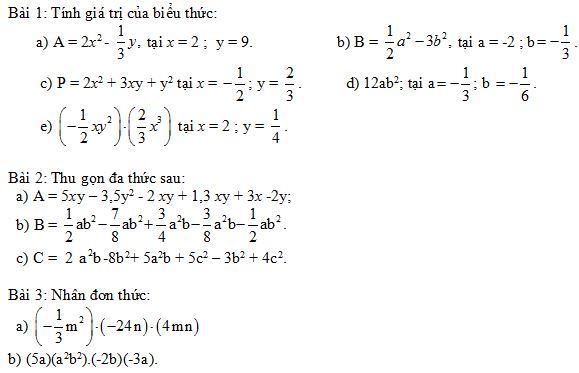
Bài 4: Tính tổng của các đa thức:

• A = x²y – xy² + 3 x² 
• B = x²y + xy² – 2 x² – 1

Bài 5: Cho: 

• P = 2x² – 3xy + 4y² ; 
• Q = 3x² + 4 xy – y² ; 
• R = x² + 2xy + 3 y².

Tính: P – Q + R.

Bài 6: Cho hai đa thức: M = 3,5x²y – 2xy² + 1,5 x²y + 2 xy + 3 xy²

N = 2 x²y + 3,2 xy + xy² – 4 xy² – 1,2 xy.

a) Thu gọn các đa thức M và N.

b) Tính M – N.

Bài 7: Tìm tổng và hiệu của: 

• P(x) = 3x² +x – 4
• Q(x) = -5 x² +x + 3.

Bài 8: Tính tổng các hệ số của tổng hai đa thức:

• K(x) = x³ – mx + m²
• L(x) =(m + 1) x² +3m x + m².

Câu 9. Cho f(x) = (x – 4) – 3(x + 1). Tìm x sao cho f(x) = 4.

Bài 10: Tìm nghiệm của đa thức:

a) g(x) = (6 – 3x)(-2x+ 5) 

b) h(x) = x² + x.

Câu 11. Cho: 

• f(x) = 9 – x^5 + 4 x – 2 x³ + x² – 7 x^4;
• g(x) = x^5 – 9 + 2 x² + 7x^4 + 2 x³ – 3 x.

a) Sắp xếp 2 đa thức f(x) và g(x) theo lũy thừa giảm dần của biến.

b) Tính tổng: h(x) = f(x) + g(x).

c) Tìm nghiệm của đa thức h(x).

Câu 12: Cho các đa thức: f(x) = x³ – 2x² + 3x + 1

g(x) = x³ + x – 1

h(x) = 2×2 – 1

a) Tính: f(x) – g(x) + h(x)

b) Tìm x sao cho f(x) – g(x) + h(x) = 0

Câu 13:

Cho P(x) = x³ – 2x + 1 ; Q(x) = 2x² – 2x³ + x – 5.

Tính: 

a) P(x) + Q(x) 

b) P(x)-Q(x)

Câu 14: Cho hai đa thức:

A(x) = –4x^5 – x³ + 4x² + 5x + 9 + 4x^5 – 6x² – 2

B(x) = –3x^4 – 2x³ + 10x² – 8x + 5x³ – 7 – 2x³ + 8x

a)Thu gọn 2 đa thức trên rồi sắp xếp chúng theo lũy thừa giảm dần của biến

b) Tính P(x) = A(x) + B(x) và Q(x) = A(x) – B(x)

c) Chứng tỏ rằng x = –1 là nghiệm của đa thức P(x).

Câu 15:

Cho f(x) = x³ − 2x + 1 và g(x) = 2x² − x3 + x −3

a) Tính f(x) + g(x) ; f(x)−g(x).

b) Tính f(x) +g(x) tại x = –1; x = -2

Câu 16:  Cho đa thức

M = x² + 5x^4 − 3x³ + x² + 4x^4 + 3x³ − x + 5

N = x − 5x³ − 2x² − 8x^4 + 4x³ − x + 5

a) Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến

b) Tính M + N và M – N

III – Hình học lớp 7 – Học kỳ 2

Bài 1: Cho tam giác ABC có CA = CB = 10cm và AB = 12cm. Kẻ đoạn thẳng CI vuông góc với AB (I ∈ AB)

a) Chứng minh IA = IB

b) Tính độ dài IC.

c) Kẻ IH vuông góc AC (H ∈ AC), kẻ IK vuông góc cùng với BC (K ∈ BC).

So sánh các độ dài cạnh IH và IK.

Bài 2: Cho tam giác ABC cân tại điểm A. Trên cạnh AB lấy điểm D, cạnh AC lấy điểm E sao cho: AD = AE

a) Chứng minh rằng BE = CD.

b) Chứng minh rằng ∠ABE = ∠ACD.

c) Gọi K là giao điểm của đoạn thẳng BE và CD. Tam giác KBC là tam giác gì? Giải thích?

Bài 3: Cho tam giác ABC vuông tại C, có góc A bằng 60°. Tia phân giác của góc BAC cắt BC tại điểm E. Kẻ EK vuông góc với AB (K ∈ AB). Kẻ BD vuông góc cùng với tia AE (D ∈ tia AE). C/M:

a) AC = AK và AE vuông góc CK.

b) KA = KA

c) EB > AC.

d) Ba đường thẳng AC, BD và KE cùng đi qua một điểm

Bài 4: Cho tam giác nhọn ABC. Vẽ ra phía ngoài ΔABC là ΔABD và ΔACE là hai tam giác đều. Gọi giao điểm của BE và DC là M. Chứng minh rằng:

a) ΔABE = ΔADC

b) ∠BMC = 120°

Bài 5: Cho ΔABC vuông tại C, có ∠A = 600, tia phân giác của góc BAC cắt BC tại E, kẻ EK vuông góc với đoạn thẳng AB. (K ∈ AB), kẻ BD vuông góc với AE (D ∈AE). Chứng minh: 

a) AK = KB                 

b) AD = BC

Bài 6: Cho ΔABC cân tại A và hai đường trung tuyến CN, BM cắt nhau tại K

a) Chứng minh ΔBNC = ΔCMB

b) Chứng minh ΔBKC cân tại K

c) Chứng minh BC < 4KM

Bài 7: Cho ΔABC vuông tại A, BD là phân giác, kẻ DE⊥BC (E ∈ BC). Gọi giao điểm của AB và DE là F. Chứng minh rằng:

a) BD là trung trực của AE

b) DF = DC

c) AD < DC;

d) AE // FC.

Bài 8: Cho tam giác ABC vuông tại A, ∠B = 600. Vẽ AH vuông góc với BC, (H ∈ BC).

a) So sánh AB và AC; BH và HC;

b) Lấy điểm D ∈ tia đối của tia HA sao cho: HD = HA. Chứng minh ΔAHC = ΔDHC.

c) Tính số đo của ∠ BDC.

Bài 9: Cho ΔABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc cùng với AB tại E, kẻ MF vuông góc cùng với AC tại F.

a) Chứng minh ΔBEM = ΔCFM.

b) Chứng minh AM là trung trực của EF.

c) Từ B kẻ đường thẳng vuông góc cùng với AB tại B, từ C kẻ đường thẳng vuông góc cùng với AC tại C, hai đường thẳng này cắt nhau tại điểm D. Chứng minh rằng ba điểm A, M, D thẳng hàng với nhau.

Bài 10: Cho tam giác ABC cân tại điểm A, đường cao AH. Biết rằng AB = 5cm, BC = 6 cm.

a) Tính độ dài các đoạn thẳng AH, BH?

b) Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng ba điểm A, G, H thẳng hàng với nhau.

c) Chứng minh hai ∠ABG = ∠ACG

Bài 11: Cho ΔABC (∠A = 900); BD là phân giác của ∠B (D∈AC). Trên tia BC lấy điểm E sao cho AB = EB.

a) Chứng minh DE ⊥ BE.

b) Chứng minh BD là đường trung trực của đoạn AE.

c) Kẻ AH ⊥ BC. So sánh EH và EC.

Bài 12: Cho tam giác nhọn ABC có AB > AC, đường cao AH.

a) Chứng minh HB > HC

b) So sánh ∠BAH và ∠CAH.

c) Vẽ M và N sao cho AB, AC lần lượt là trung trực của các đoạn thẳng HM và HN. Chứng minh rằng tam giác MAN là tam giác cân.

Bài 13: Cho tam giác nhọn ABC có AB > AC và đường cao AH.

a) Chứng minh HB > HC

b) So sánh góc BAH và góc CAH.

c) Vẽ M và N sao cho AB, AC lần lượt là trung trực của hai đoạn thẳng HM, HN.

Chứng minh rằng ΔMAN là tam giác cân.

Bai 14: Cho ∠xOy nhọn, trên 2 cạnh Ox, Oy lần lượt lấy điểm A và B sao cho OA = OB, tia phân giác của ∠xOy cắt AB tại I.

a) Chứng minh OI ⊥ AB .

b) Gọi D là hình chiếu của điểm A trên cạnh Oy, C là giao điểm của AD và OI. Chứng minh BC⊥Ox

Bài 15: Cho tam giác ABC có ∠A = 90o , AB = 8cm, AC = 6cm .

a) Tính BC.

b) Lấy điểm E trên cạnh AC sao cho: AE = 2cm; lấy điểm D trên tia đối của tia AB  sao cho AD = AB. Chứng minh rằng: ΔBEC = ΔDEC.

c) Chứng minh rằng DE đi qua trung điểm của cạnh BC.

C. Đề thi học kì 2 Toán 7 tham khảo (Có đáp án)

Đề ôn thi học kì 2 Toán 7 – Tham khảo:

Đáp án đề ôn thi học kì 2 Toán 7 – Tham khảo:

Trên đây là Đề cương ôn thi học kì 2 toán 7 do HOCTOT tổng hợp và biên soạn. Các bạn học sinh hãy tham khảo và ôn luyện thật kỹ các dạng bài thật chăm chỉ để đạt được kết quả tốt nhất nhé!