Đường kính và dây của đường tròn là kiến thức quan trọng trong chương trình hình học Toán lớp 9. Trong bài viết này, HOCMAI đã tổng hợp những kiến thức lý thuyết cần nhớ và các dạng bài tập quan trọng liên quan đến Đường kính và dây của đường tròn.
A. Tóm tắt lý thuyết về đường kính và dây của đường tròn
1. Cung và dây cung của đường tròn
Cho đường tròn tâm O. Nếu hai điểm A,B phân biệt nằm trên đường tròn thì chúng chia đường tròn thành hai phần, mỗi phần là một cung.
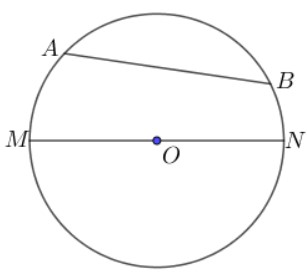
Trong đó:
- Hai điểm A và B chính là hai mút của cung.
- Đoạn thẳng nối hai điểm mút của cung được gọi là dây cung.
- Dây cung đi qua tâm đường tròn gọi là đường kính.
Tham khảo ngay kiến thức cơ bản của đường tròn tại: Đường tròn là gì?
2. Dây cung và đường kính của một đường tròn
a) Trong một đường tròn, đường kính dài gấp đôi bán kính
D = 2r
Định lý 1: Trong tất cả các dây của đường tròn, dây có độ dài lớn nhất là đường kính.
Xét đường tròn (O ; R):
- A thuộc (O ; R)
- B thuộc (O ; R)
Suy ra AB ≤ 2R
b) Quan hệ vuông góc của dây và đường kính
Định lý 2: Trong một đường tròn, đường kính vuông góc với dây nào thì đi qua trung
điểm của dây ấy.
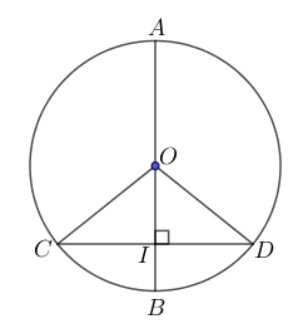
Chứng minh định lý:
- Trường hợp 1: Nếu dây CD là đường kính, chắc chắn AB đi qua trung điểm O của CD.
- Trường hợp 2: Nếu CD không là đường kính.
Gọi giao điểm của AB và CD là I. Tam giác OCD có OC = OD = R
=> Tam giác OCD cân tại O
=> OI đường cao nên cũng là đường trung tuyến
=> IC = ID.
Định lý 3: Trong một đường tròn, đường kính đi qua trung điểm của dây nào mà không
đi qua tâm thì đường kính vuông góc với dây ấy.
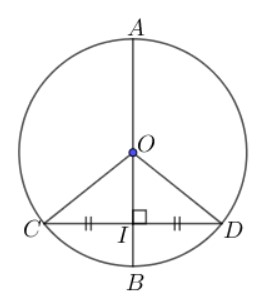
Chứng minh định lý:
Gọi I là giao điểm của dây CD và đường kính AB.
=> ΔOCD cân tại O (Vì OC = OD)
Mà OI là trung tuyến nên OI đồng thời là đường cao. Do đó cạnh OI vuông góc với cạnh CD tại I.
Chú ý: Đường kính đi qua trung điểm của một dây có thể không vuông góc với dây ấy.
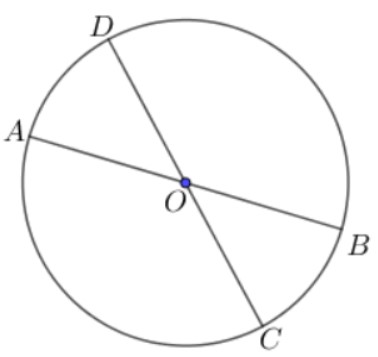
Giả sử AB, CD là đường kính của đường tròn tâm O. Khi đó CD cũng là dây cung của đường tròn.
Mà O thuộc CD và OC = OD (Vì CD là đường kính)
=> O là trung điểm của CD
Khi đó, đường kính AB đi qua trung điểm O của dây CD nhưng AB và CD không vuông góc với nhau.
Liên hệ khoảng cách từ tâm đường tròn đến dây
a) Trong một đường tròn:
+ Hai dây có kích thước bằng nhau thì cách đều tâm.
+ Hai dây cùng cách đều tâm thì bằng nhau.
b) Trong hai dây cùng một đường tròn:
+ Dây nào có kích thước lớn hơn thì dây đó gần tâm hơn.
+ Dây nào gần với tâm hơn thì dây đó có kích thước lớn hơn.
B. Các dạng bài thường gặp liên quan đến đường kính và dây của đường tròn
Để giải được các dạng toán này, chúng ta cần nắm vững và vận dụng một số kiến thức về:
- Quan hệ vuông góc của đường kính và dây
- Định lý Pytago.
- Hệ thức lượng sử dụng trong tam giác vuông.
Dạng 1: Các bài toán có liên quan đến tính toán trong đường tròn
Ví dụ 1: Cho đường tròn (O) có bán kính. Dây HK của (O) vuông góc với OI tại trung điểm của OI. Tính độ dài dây HK?
Lời giải:

Ví dụ 2: Cho đường tròn (O) với đường kính là AD = 2R. Vẽ cung tâm D và bán kính R. Cung này cắt đường tròn (O) tại 2 điểm B và C.
a) Tứ giác OBDC là hình gì? Vì sao?
b) Tính số đo góc CBD, góc CBO, góc OBA?
c) Chứng minh ΔABC là tam giác đều?
Lời giải:

Dạng 2: Chứng minh rằng hai đoạn thẳng không bằng nhau
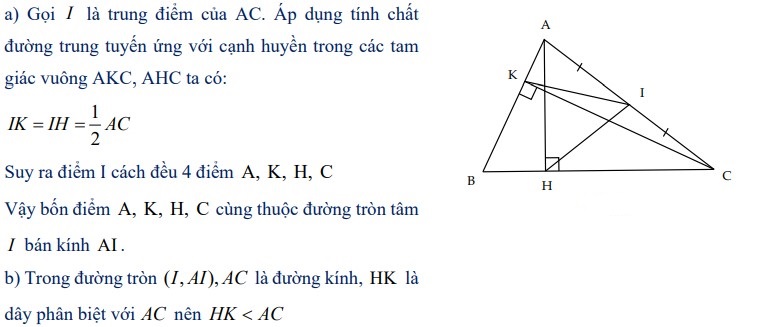
Ví dụ 1: Cho tam giác ABC, các đường cao AH và CK. Chứng minh rằng:
a) 4 điểm A,C, H và K cùng thuộc một đường tròn;
b) HK < AC.
Lời giải:
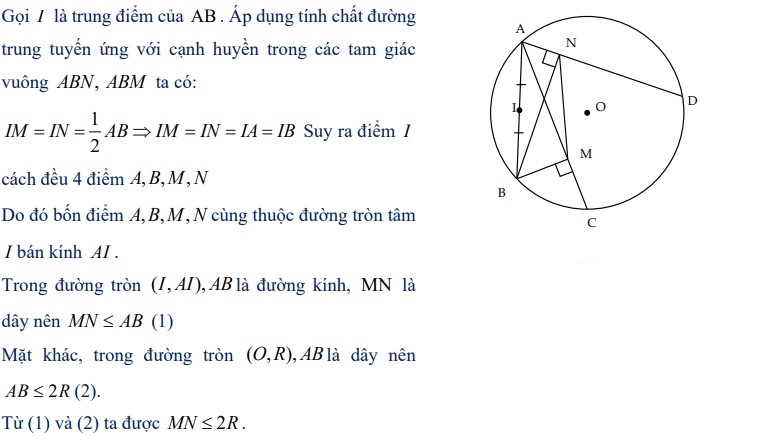
Ví dụ 2: Cho đường tròn (O;R) và ba dây AB, AC, AD; gọi M và N lần lượt là hình chiếu của B trên các đường thẳng AC, AD. Chứng minh rằng MN ≤ 2R.
Dạng 3: Chứng minh rằng hai đoạn thẳng bằng nhau
Ví dụ 1: Cho nửa đường tròn tâm (O), đường kính AB và dây EF không cắt đường kính. Gọi điểm I và điểm K lần lượt là chân các đường vuông góc kẻ từ điểm A và điểm B đến dây EF. Chứng minh rằng IE = KF.
Lời giải:

Ví dụ 2: Cho đường tròn (O) và dây AB không đi qua tâm. Gọi M là trung điểm của AB. Qua điểm M vẽ dây CD (không trùng với AB). Chứng minh rằng điểm M không phải là trung điểm của dây CD.
Lời giải:

Bài viết tham khảo thêm:
- Tổng hợp kiến thức toán 9
- Phương pháp chứng minh tứ giác nội tiếp
- Sự xác định đường tròn. Tính chất đối xứng của đường tròn
HOCMAI cảm ơn bạn đã quan tâm và theo dõi bài viết về chủ đề Đường kính và dây của đường tròn. Mong rằng bài viết sẽ tư liệu tham khảo và ôn tập bổ ích dành cho các bạn học sinh. Đừng bỏ lỡ những bài viết mới nhất trên hoctot.hocmai.vn bạn nhé!


















