Chuyên đề Sự xác định đường tròn. Tính chất đối xứng của đường tròn là một trong những chuyên đề quan trọng trong chương trình Toán lớp 9 và tài liệu ôn thi vào lớp 10. Trong bài viết này, các bạn sẽ cùng HOCMAI ôn lại các kiến thức cần nhớ, các dạng bài tập thường gặp về đường tròn.
I. Kiến thức cần nhớ về sự xác định đường tròn. Tính chất đối xứng của một đường tròn
1. Định nghĩa về đường tròn
Đường tròn tâm O bán kính R (với R >0), kí hiệu (O;R), – Là hình gồm các điểm cách tâm O một khoảng bằng R.
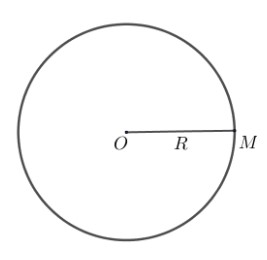
Tổng quát:
Đường tròn (O;R) = {M|OM = R}. Kí hiệu (O;R)
2. Vị trí tương đối giữa một điểm với một đường tròn
Có 3 vị trí của 1 điểm trên đường tròn. Bao gồm:
- Nếu điểm M nằm trên đường tròn (O;R) => OM=R
- Nếu điểm M nằm trong đường tròn (O; R) => OM<R
- Nếu điểm M nằm ngoài đường tròn (O;R) => OM>R.
3. Định lý về cách xác định một đường tròn
a. Đường tròn đi qua 2 điểm
Đường tròn đi qua hai điểm có tâm nằm trên đường trung trực của đoạn thẳng có hai mút là điểm đó.
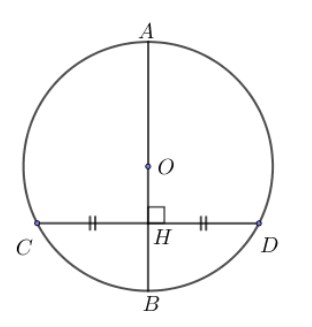
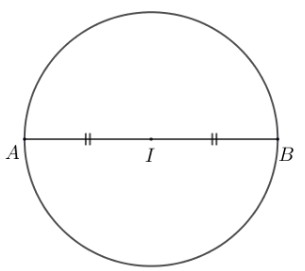
Trường hợp đặc biệt: Tâm của đường tròn là trung điểm của đoạn thẳng AB và bán kính bằng AB/2.
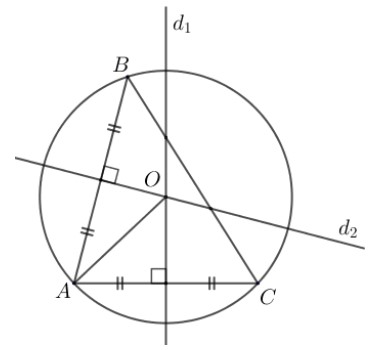
b. Đường tròn đi qua ba điểm
Tâm của đường tròn đi qua ba điểm A, B, C không thẳng hàng chính là giao điểm các đường trung trực của tam giác ABC.
Bán kính là khoảng cách tính từ tâm tới 1 trong 3 đỉnh của tam giác. Kí hiệu: (O; OA).
Vậy nên, một đường tròn chỉ được xác định khi biết tâm và bán kính của đường tròn đó, hoặc khi biết một đoạn thẳng chính là đường kính của đường tròn đó.
Định lý: Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
Chú ý: Không thể vẽ được một đường tròn nào đi qua ba điểm thẳng hàng.
4. Đường tròn ngoại tiếp tam giác
Đường tròn đi qua ba đỉnh A, B, C của ΔABC được gọi là đường tròn ngoại tiếp ΔABC.
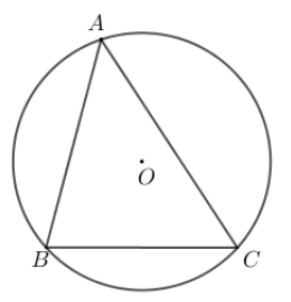
Khi đó ΔABC gọi là tam giác nội tiếp đường tròn.
Trường hợp đặc biệt:
- Tâm của đường tròn ngoại tiếp Δ vuông là trung điểm của cạnh huyền.
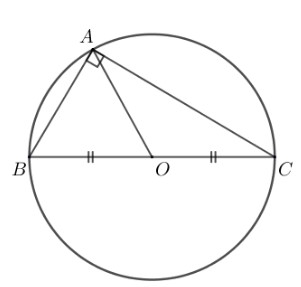
- Tâm của đường tròn ngoại tiếp Δ cân nằm trên đường cao của tam giác cân đó.
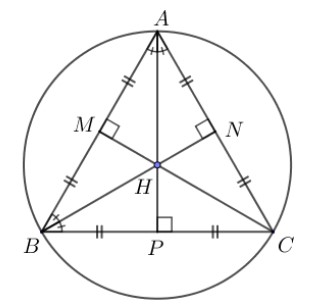
- Tâm của đường tròn ngoại tiếp Δ đều trùng với trong tâm, trực tâm, tâm của đường tròn nội tiếp tam giác đó.
5. Các tính chất đối xứng của một đường tròn
a. Tâm đối xứng của đường tròn
Đường tròn là một hình có tâm đối xứng. Tâm của đường tròn cũng chính là tâm đối xứng của đường tròn đó.

Vậy nên, đường tròn chỉ có duy nhất một tâm đối xứng.
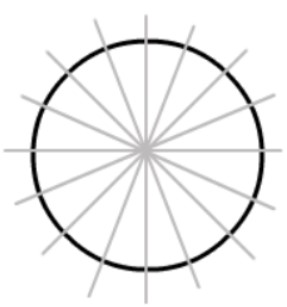
b. Trục đối xứng của đường tròn
Đường tròn là một hình có trục đối xứng. Bất kỳ một đường kính nào cũng sẽ là trục đối xứng của đường tròn. Chính vì vậy, một đường tròn có vô số trục đối xứng!
II. CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1: Chứng minh các điểm cho trước cùng thuộc một đường tròn
Để giải dạng toán này, chúng ta cần chứng minh các điểm cho trước cùng cách đều một điểm nào đó. Điểm đó chính xác là tâm của đường tròn.
Ví dụ: Cho ΔABC (vuông tại A). Lấy điểm D trên cạnh AC. Hình chiếu của điểm D lên BC là điểm E, điểm đối xứng của E qua cạnh BD là F. Chứng minh rằng 5 điểm A, B, E, D và F cùng nằm trên một đường tròn. Sau đó hãy xác định tâm O của đường tròn đó.
Lời giải:
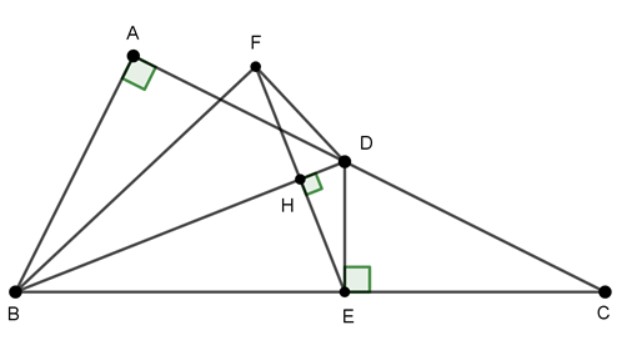
Theo bài ra ta có: ΔBAD có góc A bằng 90 độ và A nằm trên đường tròn đường kính BD.
- ΔBED có góc E bằng 90 độ (E là hình chiếu của D lên BC) ⇒ E nằm trên đường tròn đường kính BD.
- F đối xứng với E qua cạnh BD nên điểm F cũng nằm trên đường tròn đường kính BD (tính chất đối xứng của đường tròn).
Vậy: Năm điểm A, B, E, D, F cùng nằm trên đường tròn đường kính BD và tâm O là trung điểm của BD.
Dạng 2: Xác định vị trí tương đối giữa một điểm đối với đường tròn
Để xác định vị trí tương đối của điểm M đối với đường tròn (O ; R), ta sẽ so sánh độ dài khoảng cách OM với bán kính R theo:
| Vị trí tương đối | Hệ thức |
| M nằm trên đường tròn (O ; R) | OM=R |
| M nằm trong đường tròn (O ; R) | OM<R |
| M nằm ngoài đường tròn (O ; R) | OM>R |
Ví dụ:

Dạng 3: Đường kính và dây của một đường tròn. Liên hệ khoảng cách tính từ tâm đến dây
Để làm dạng toán này, chúng ta sẽ cần sử dụng:
- Tính chất về đường trung tuyến trong một tam giác vuông.
- Định lý Pytago.
- Hệ thức lượng về góc và cạnh trong một tam giác vuông.
Ví dụ: Cho đường tròn tâm O, bán kính bằng 5 cm và dây AB = 8 cm .
- a) Tìm khoảng cách tính từ O đến AB .
- b) Gọi I là một điểm thuộc dây AB với AI = 1 cm. Kẻ dây CD đi qua điểm I và vuông góc với cạnh AB. Chứng minh CD = AB.
Lời giải:

Tham khảo thêm:
Bài viết này là bài tổng hợp các kiến thức trọng tâm, liệt kê và chỉ dẫn giải các dạng bài tập thường gặp của chuyên đề Sự xác định đường tròn. Tính chất đối xứng của đường tròn. Mong rằng bài viết của HOCMAI sẽ hỗ trợ cho các bạn học sinh trong quá trình học tập chương trình Toán 9 và ôn thi vào lớp 10 môn toán.





















