Tỉ số lượng giác của góc nhọn (hay còn gọi hệ thức lượng giác) được Bộ Giáo dục đưa vào chương trình học từ lớp 9 đến đến hết lớp 12. Vì vậy, các em học sinh cần phải hiểu được khái niệm, tính chất, và các công thức vận dụng về lượng giác. Dưới đây sẽ là những kiến thức chi tiết và cơ bản nhất về lượng giác mà HOCMAI đã tổng hợp cho các em học sinh tham khảo. Cùng vào bài thôi nào!
I. Khái niệm về tỉ số lượng giác góc nhọn
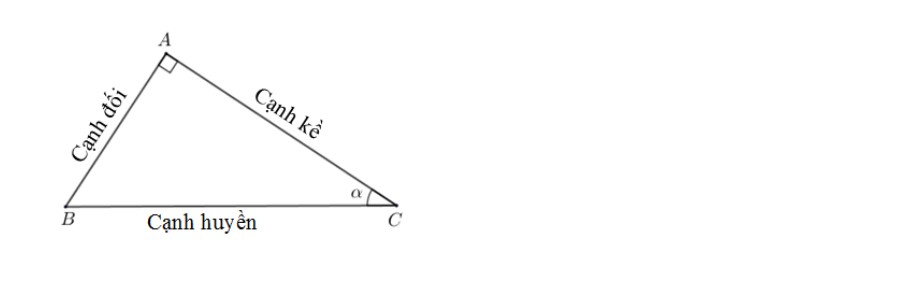
1. Định nghĩa về tỉ số lượng giác của góc nhọn
Tỉ số lượng giác của góc nhọn là các tỉ số của góc nhọn và các cạnh tương ứng xuất hiện trong các tam giác vuông.
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sin α.
Tỉ số giữa cạnh kề và cạnh huyền được gọi là cos (cosin) của góc α, kí hiệu là cos α.
Tỉ số giữa cạnh đối và cạnh kề được gọi là tan (tang) của góc α, kí hiệu là tan α.
Tỉ số giữa cạnh kề và cạnh đối được gọi là cot (côtang) của góc α, kí hiệu là cot α.
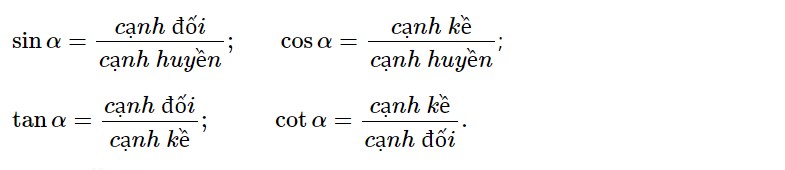
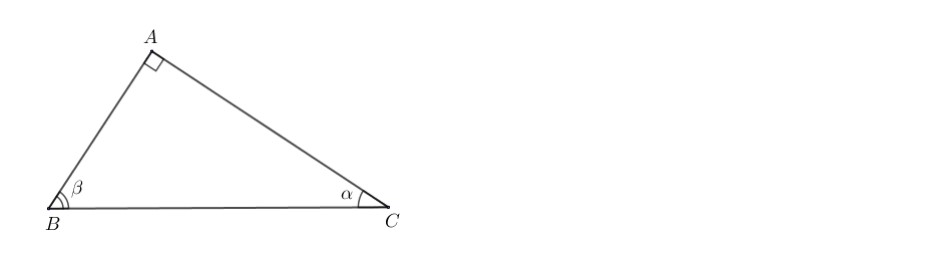
Ví dụ: Cho tam giác ABC vuông tại A, gọi góc ACB là α. (như hình 1)
Góc α có:
- AC là cạnh kề
- AB là cạnh đối
- BC là canh huyền
Sin α = AB/BC (tỉ số cạnh đối với cạnh huyền)
Cos α = AC/BC (tỉ số cạnh kề với cạnh huyền)
Tan α = AB/AC (tỉ số cạnh đối với cạnh kề)
Cot α = AC/AB (tỉ số cạnh kề với cạnh đối)
2. Tính chất của tỉ số lượng giác của góc nhọn
Tính chất 1:
Nếu hai góc phụ nhau (tổng hai góc bằng 90 độ), thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
Ví dụ: Cho 2 góc α β, α + β = 90o
Khi đó:
sinα = cosβ, cosα = sinβ, tanα = cotβ, cotα = tanβ
Tính chất 2:
Nếu: hai góc α = β
Thì: sinα = sinβ, cosα = cosβ
Tính chất 3:
Nếu α là góc nhọn bất kỳ trong một tam giác vuông, ta có những công thức sau:
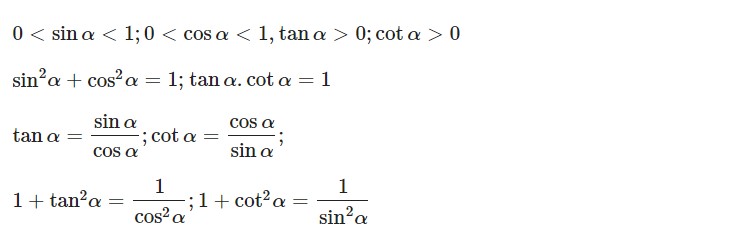
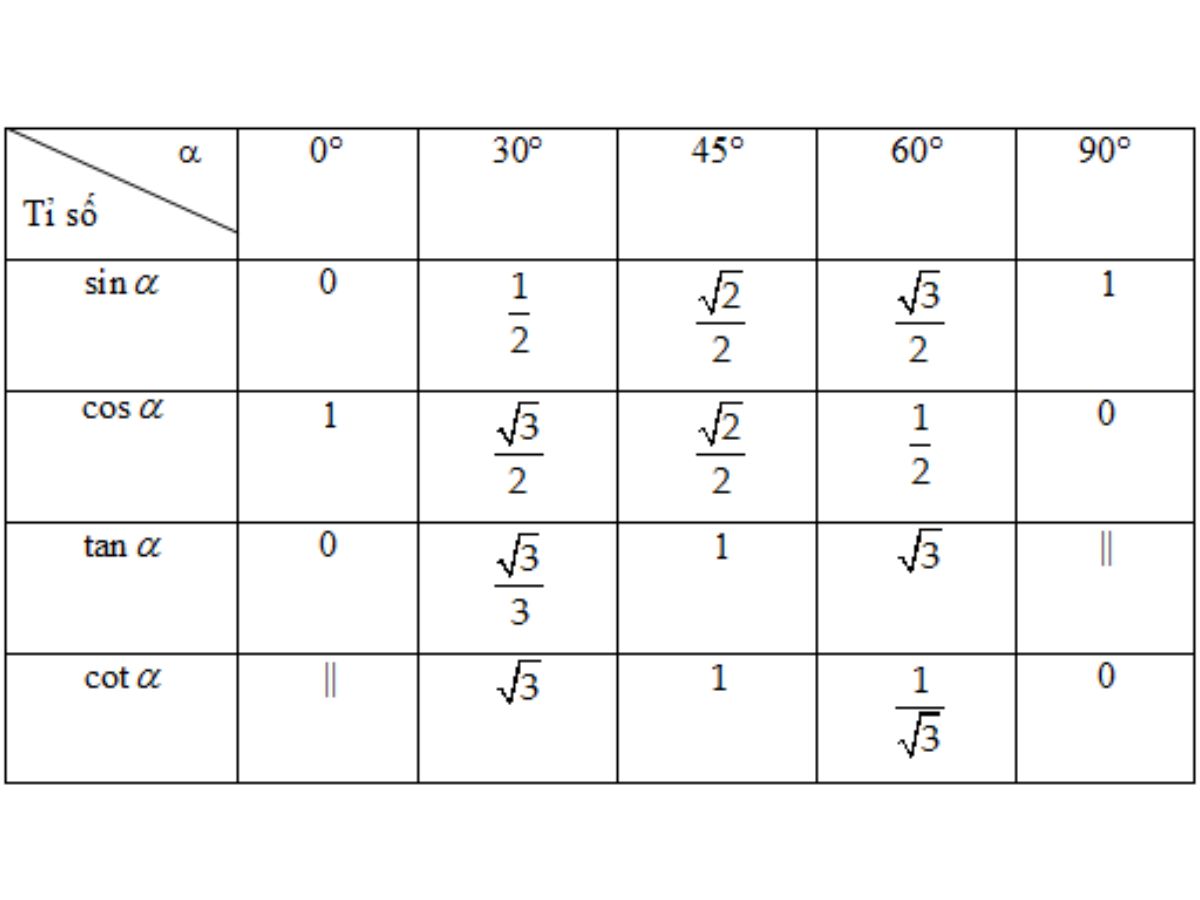
Bảng tỉ số lượng giác các góc đặc biệt
Tỉ số lượng giác của góc nhọn trong tam giác đều
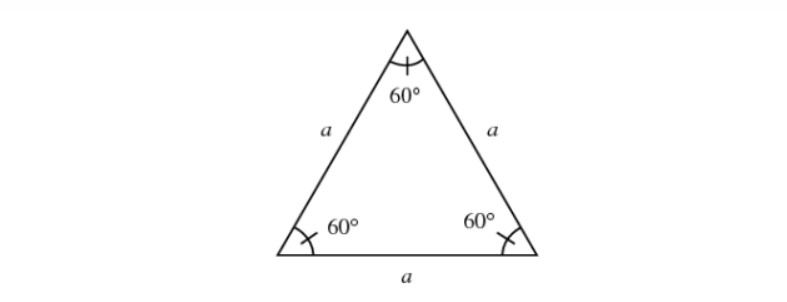
Ta có tam giác đều có ba góc đều bằng α = 60o
Vậy suy ra:
Sin α = √3/2
Cos α = 1/2
Tan α = √3
Cot α = 1/√3
3. Một số hệ thức cơ bản
Cho α là một góc nhọn bất kỳ, ta được những hệ thức như sau:
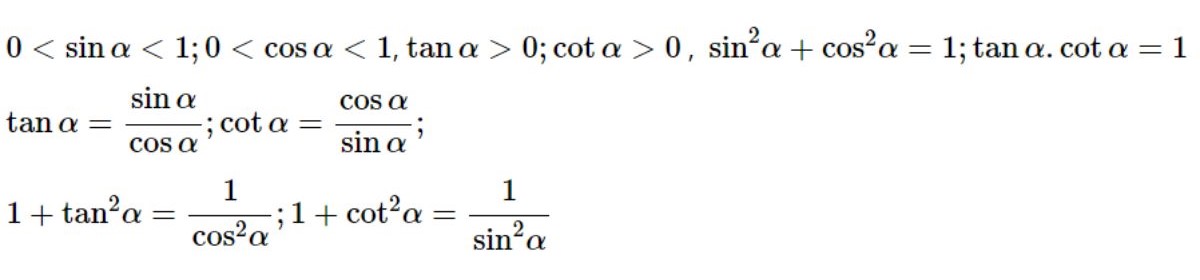
4. So sánh các tỉ số lượng giác
- a) Cho hai góc nhọn của một tam giác vuông là α,β. Nếu α < β thì
sinα < sinβ; tanα < tanβ
cosα > cosβ; cotα > cotβ
- b) sinα < tanα; cosα < cotα
5. Hệ thức về góc và cạnh trong tam giác vuông

II. Một số bài tập minh họa về tỉ số lượng giác của góc nhọn
Bài 1: Cho tam giác ABC, góc BAC bằng 90 độ, góc ACB bằng 30 độ, biết BC = 10cm. Tính AB, AC.
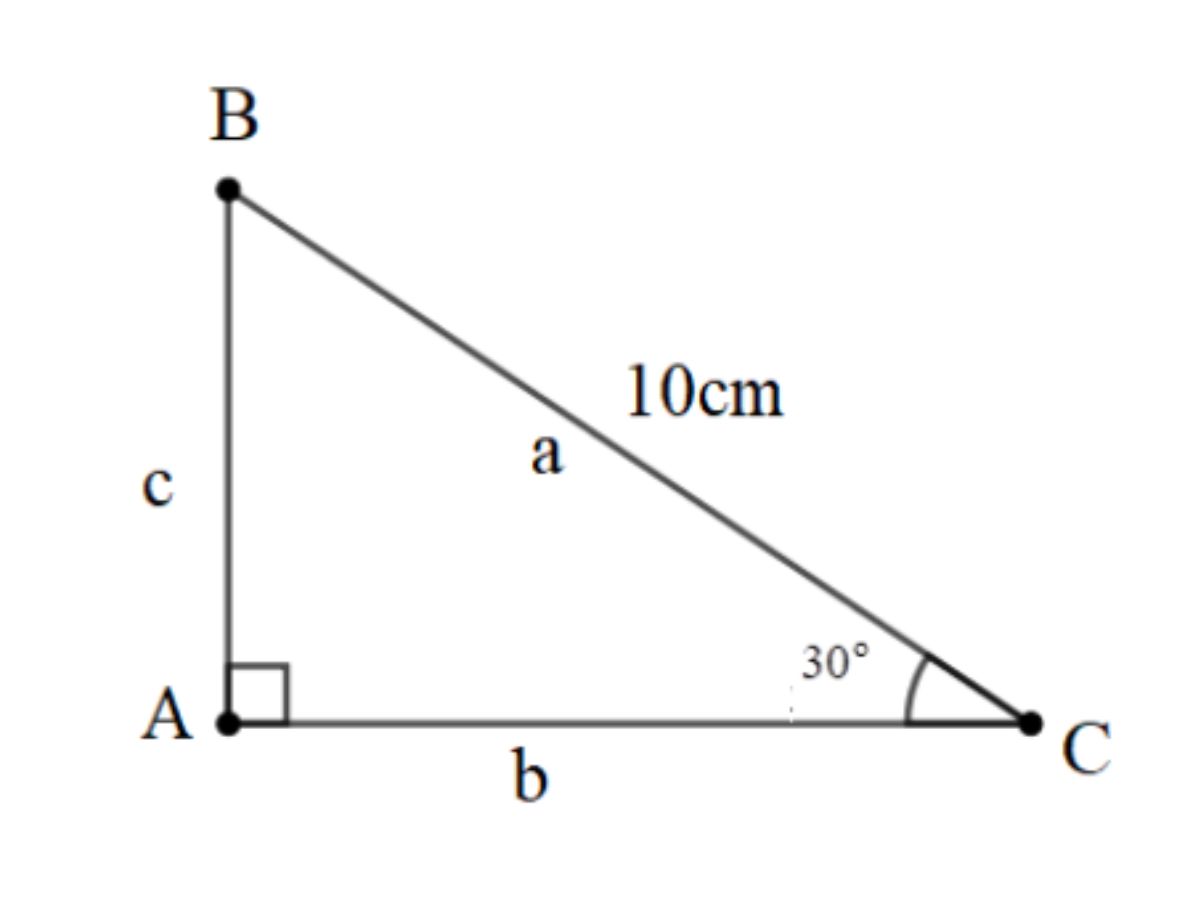
Hướng dẫn giải:
Ta có:
c = a.sinC
⇒c = 10.sin30°
⇒c = 10.1/2
⇒c = AB = 5 (cm)
b = a.cosC
⇒b = 10.cos30°
⇒b = 10.√3/2
⇒b = AC = 5√3 (cm)
Bài 2: Cho tam giác ABC có AH là đường cao ứng với cạnh BC. Biết góc ABC bằng 30 độ, AB = 10cm. Tính BH.
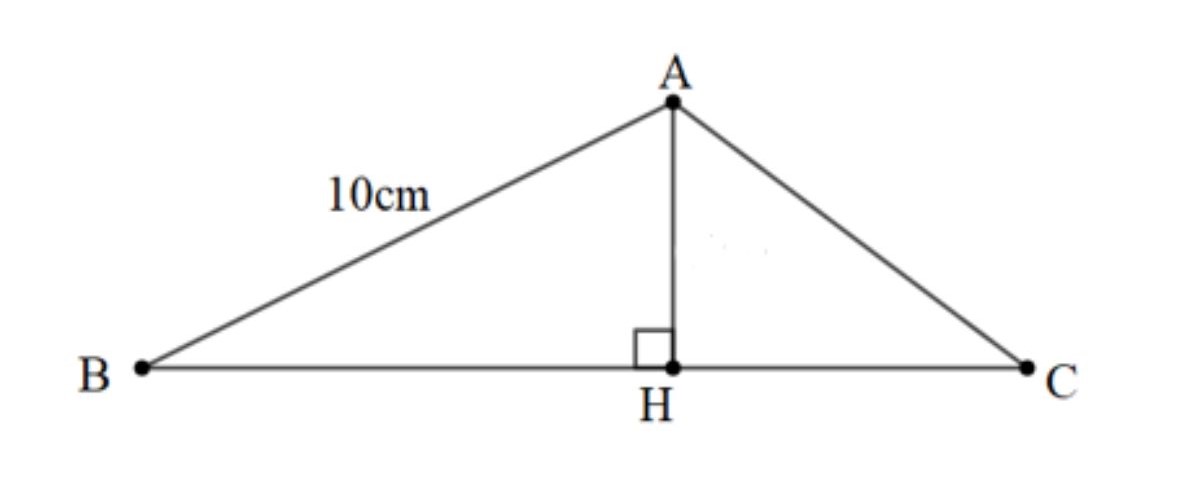
Hướng dẫn giải:
Xem tam giác ABH vuông tại H (do AH là đường cao)
Áp dụng hệ thức giữa góc và cạnh trong tam giác vuông:
BH = AB cosB
⇒BH = 10.cos30°
⇒BH = 10.√3/2 = 5√3 (cm)
Bài 3: Cho tam giác ABC có góc ABC bằng 60 độ. Hình chiếu của cạnh AB trên BC có độ dài là 4cm, AB dài gấp đôi AC. Tính độ dài AB, AC và góc ACB.
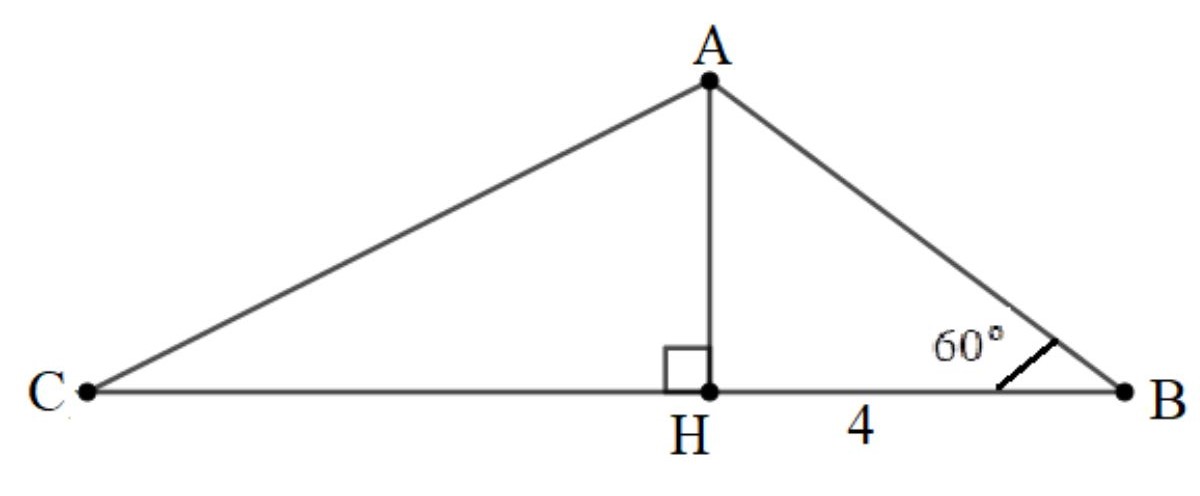
Tạo đường cao AH, HB là hình chiếu của AB trên BC
Xét tam giác AHB có góc AHB bằng 90 độ, có:
HB = AB.cosB
⇒AB = HB/cosB
⇒AB = 4/cos40°
⇒AB = 8 (cm)
AH = AB.sinB
⇒AH = 8.sin60°
⇒AH = 8.√3/2 = 4√3 (cm)
Theo đề bài ta có: AC = 2AB AC = 2.8 = 16 (cm)
Xét tam giác AHC có:
AH = AC.sinC
⇒sinC = AH/AC
⇒sinC = 4√3/16 = √3/4
⇒góc ACB ≈ 25°39’
Những kiến thức bổ ích khác các em có thể tham khảo:
Một số hệ thức về cạnh và đường cao trong tam giác vuông
Bài viết trên đây đã tổng hợp đầy đủ kiến thức, công thức và một số bài tập tham khảo về tỉ số lượng giác của góc nhọn. Các em học sinh hãy cố gắng chăm chỉ luyện các dạng bài tập về lượng giác nhé, vì chúng rất hay xuất hiện trong các bài thi. Đừng quên truy cập vào hoctot.hocmai.vn để có thêm cho mình thật nhiều kiến thức bổ ích nữa nhé!
















