Là một trong những kiến thức vô cùng quan trọng trong Toán cấp THCS và chương trình học Toán 9. Hệ thức Viet thường xuất hiện trong các cuộc thi học sinh giỏi hay kỳ thi tuyển sinh vào lớp 10. Trong bài viết này, HOCMAI sẽ chia sẻ các dạng bài hệ thức Viet kèm theo ví dụ giải các dạng này để các em học sinh có thể tham khảo!
I. Lý thuyết quan trọng về Hệ thức Viet
Hệ thức Viet hay định lý Viet được một nhà toán học người Pháp – François Viète tìm ra. Định lý này thể hiện mối quan hệ giữa các nghiệm trong một phương trình đa thức. Bao gồm Định lý Viet thuận, Hệ thức Viet ngược và Hệ thức Viet đảo.
1. Hệ thức Viet thuận
Cho phương trình bậc hai một ẩn: ax^2 + bx + c = 0 (a0) có 2 nghiệm x1 và x2. Khi đó, 2 nghiệm x1,x2 thỏa mãn hệ thức sau:
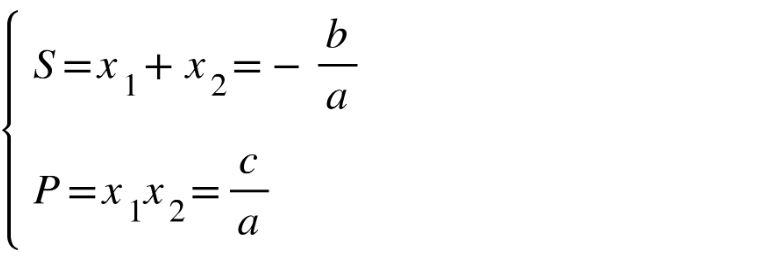
Hệ quả: Dựa vào hệ thức Viet, ta có thể nhẩm luôn nghiệm của phương trình trong một số trường hợp đặc biệt khi phương trình bậc 2 một ẩn có nghiệm:

2. Hệ thức Viet đảo
Giả sử hai số thực x1, x2 thỏa mãn hệ thức:
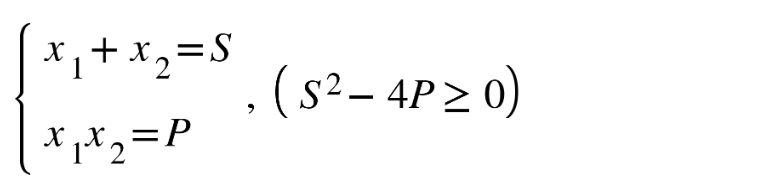
=> x1,x2 là nghiệm của phương trình bậc 2 một ẩn: x^2 – Sx + P = 0
Chú ý: S^2 – 4P ≥ 0 là điều kiện bắt buộc để phương trình bậc hai tồn tại 2 nghiệm là x1 và x2.
II. Các dạng bài tập hệ thức Viet (có kèm ví dụ)
Sau khi bạn đã nắm được những kiến thức quan trọng, tiếp theo chúng ta sẽ cùng tìm hiểu về các dạng bài tập hệ thức Viet hay gặp.
Dạng 1: Tính nhẩm nghiệm dựa vào hệ thức Viet
Khi giải các bài toán giải phương trình bậc 2, chúng ta thường sử dụng biệt thức Δ để suy ra các nghiệm x1, x2 (nếu có). Tuy nhiên bạn có thể dễ dàng tính nhẩm nhanh hơn nhờ hệ thức Viet. (Áp dụng hệ quả của hệ thức Viet thuận ở phần I)

Nhận xét: Qua 2 ví dụ, phương pháp này có thể giúp bạn giải các phương trình đặc biệt trở nên dễ dàng và nhanh chóng.
Dạng 2. Tìm giá trị của biểu thức giữa các nghiệm
Nếu phương trình ax^2 + bx + c = 0 ( a ≠ 0) có hai nghiệm x1 và x2, ta có thể thể hiện các biểu thức đối xứng giữa các nghiệm theo S = x1 + x2 và P = x1.x2.

Chú ý: Khi tìm giá trị một biểu thức giữa các nghiệm thông thường, ta phải biến đổi sao cho xuất hiện tổng và tích các nghiệm trong biểu thức đó rồi áp dụng định lý Viet.
Dạng 3: Tìm hai số sau khi biết tổng và tích
Theo hệ thức Vi-ét, ta có:
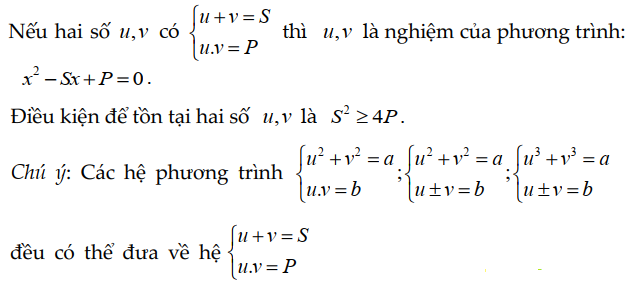
Ví dụ: Cho hình chữ nhật ABCD với diện tích và chu vi lần lượt là là 2a2 và 6a. Hãy tìm các kích thước của hình chữ nhật.
Lời giải
Gọi x, y lần lượt là các kích thước của hình chữ nhật ABCD ( x, y > 0)

Dạng 4: Ứng dụng phân tích tam thức bậc hai thành nhân tử
Thí dụ ta có: ax^2 + bx + c = 0 có Δ ≥ 0 ( a ≠ 0)
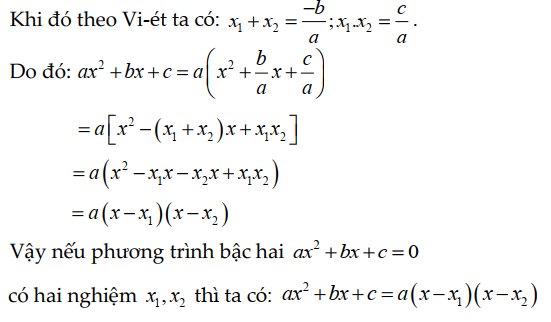
Ví dụ: Phân tích phương trình: 3x^2+ 5x – 8 thành nhân tử?
Lời giải:
Dựa vào đề ta có: 3x^2+ 5x – 8 = 0 có a + b + c = 3 + 5 – 8 = 0 => Phương trình có 2 nghiệm là x1 = 1 và x2 = c/a = -8/3.
=> Tam thức bậc hai: 3x^2 + 5x – 8 = (x – 1)(x + 83)
Dạng 5. Tìm ĐK của tham số để phương trình bậc 2 có một nghiệm x = x1 cho trước. Tìm nghiệm thứ hai
Tìm ĐK để phương trình có nghiệm x = x1 cho trước
Có 2 cách tìm đ.kiện để phương trình có nghiệm x = x1 cho trước:
Cách 1:
- Bước 1: Tìm điều kiện để phương trình có hai nghiệm (Điều kiện ).
- Bước 2: Tìm giá trị của tham số bằng cách thay x = x1 vào phương trình.
- Bước 3: Đối chiếu giá trị tham số vừa tìm được với điều kiện (Δ ≥ 0) và kết luận
Cách 2:
- Bước 1. Thay x = x1 vào phương trình đã cho để tìm giá trị của tham số.
- Bước 2. Thay giá trị tham số vừa tìm được vào phương trình và giải.
Chú ý: Nếu Δ < 0 sau khi thay giá trị của tham số vào phương trình đã cho => Kết luận: Không có giá trị nào của tham số để phương trình có nghiệm x1 cho trước.
Tìm nghiệm thứ hai
Sau khi tìm được điều kiện, chúng ta sẽ tiến hành tìm nghiệm thứ hai bằng 3 cách:
- Cách 1: Thay giá trị của tham số vừa tìm được rồi giải phương trình.
- Cách 2: Thay g.trị của tham số vừa tìm được vào công thức tổng 2 nghiệm => nghiệm thứ 2.
- Cách 3: Thay g.trị của tham số vừa tìm được vào công thức tích hai nghiệm => nghiệm thứ 2.
Ví dụ: Với giá trị k nào thì:
a) Phương trình 2x^2 + kx – 10 = 0 có một nghiệm x = 2. Tìm nghiệm kia?
b) Phương trình (k – 5)x^2 – (k – 2)x + 2k = 0 có một nghiệm x = – 2. Tìm nghiệm kia?
c) Phương trình kx^2 – kx – 72 có một nghiệm x = – 3. Tìm nghiệm kia?
Lời giải

Dạng 6. Xác định tham số sao cho các nghiệm của phương trình bậc 2 thỏa mãn hệ một điều kiện cho trước.
“Điều kiện cho trước” là các nghiệm của phương trình bậc hai, thỏa mãn một đẳng thức hoặc bất đẳng thức hoặc để một biểu thức của các nghiệm của phương trình bậc hai đạt giá trị lớn nhất, giá trị nhỏ nhất,…

Chú ý: Khi đã tìm được tham số, bạn phải đối chiếu với điều kiện phương trình có nghiệm.
Ví dụ: Cho phương trình: x^2 – 6x + m = 0. Tìm giá trị của m biết phương trình có hai nghiệm x1, x2 thỏa mãn điều kiện: x1 – x2 = 4.
Lời giải

Dạng 7. Lập phương trình bậc hai một ẩn khi biết hai nghiệm của nó hoặc hai nghiệm có liên quan tới hai nghiệm của một phương trình đã cho.
Khi đã biết hai nghiệm là a và b, để lập phương trình bậc hai cần phải tính a + b và a.b.
Áp dụng hệ thức Viet đảo ta có: x^2 – (a + b)x + a.b = 0
Ví dụ: phương trình x2 – 7x + 3 = 0 có hai nghiệm là x1 và x2. Hãy lập phương trình bậc hai có hai nghiệm là 2×1 – x2 và 2x^2 – x1.
Lời giải

Dạng 8. Tìm hệ thức liên hệ giữa hai nghiệm của PT bậc hai không phụ thuộc vào tham số
Cách tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc vào tham số trong phương trình bậc 2:

Ví dụ: Cho phương trình 8x^2 – 4(m – 2)x + m(m – 4) = 0. Tìm m để p.trình có hai nghiệm là x1, x2. Tìm hệ thức giữa hai nghiệm độc lập với m, Từ đó suy ra vị trí của các nghiệm với hai số 1 và – 1.
Lời giải
Theo đề bài ta có phương trình bậc 2:

Dạng 9. C/m hệ thức giữa các nghiệm của PT bậc 2 hoặc hai PT bậc 2
Ví dụ: Chứng minh rằng nếu a1, a2 là các nghiệm của phương trình x^2 + px + 1 = 0 và b1, b2 là các nghiệm của phương trình x^2 + qx + 1 = 0 thì:
(a1 – b1)(a2 – b1)(a1 + b2)(a2 + b2) = q2 – p2
Lời giải

Dạng 10: Xét dấu các nghiệm của PT bậc 2, so sánh nghiệm của PT bậc 2 với một số cho trước.
Sử dụng hệ thức Viet để xét dấu các nghiệm của phương trình bậc 2: ax^2 + bx + c = 0 ( a ≠ 0) dựa trên các kết quả sau:

Ngoài ra bạn còn có thể áp dụng hệ thức Vi-ét để so sánh được nghiệm của phương trình bậc 2 với một số cho trước.
Ví dụ: Cho phương trình x^2 – (2m + 3)x + m2 + 3m + 2 = 0. Tìm m để p.trình có hai nghiệm đối nhau.
Lời giải

Dạng 11. Nghiệm chung của hai hay nhiều PT, hai PT tương đương
Ví dụ: Xác định m để hai p.trình sau tương đương với nhau:
- x^2 + 2x – m = 0
- 2x^2 + mx + 1 = 0
Lời giải

Dạng 12. Giải các bài toán số học
Ví dụ: Tìm các số nguyên dương x, y thỏa mãn phương trình x^3 + y^3 + 1 = 3xy
Lời giải

Dạng 13. Giải phương trình, hệ phương trình dựa vào hệ thức Viet

Vậy phương trình đã cho có nghiệm S= { -3;0}.
Dạng 14. Giải các bài toán tìm gtln, gtnn, chứng minh đẳng thức, bất đẳng thức.
Các bạn học sinh đã được làm quen với bất đẳng thức Cô-si, ta có thể chứng minh bất đẳng thức này dựa vào hệ thức Vi-ét:

Ví dụ: Các số x, y thỏa mãn điều kiện: x + y = 2. Hãy tìm GTNN của F = x^3 + y^3
Lời giải
Vận dụng hệ thức Viet, ta có:

Dạng 15. Vận dụng hệ thức Viet trong mặt phẳng tọa độ
Vận dụng hệ thức Viet ta có thể giải một số dạng toán trong mặt phẳng tọa độ như: viết phương trình đường thẳng; khảo sát hàm số; xét vị trí tương đối của parabol và đường thẳng.
Ví dụ: Cho (P): y = – x^2 và đường thẳng (D) có hệ số góc là a đi qua điểm M(– 1; – 2).
- a) Chứng minh: Với mọi giá trị của a thì (D) luôn cắt (P) tại hai điểm phân biệt A và B.
- b) Xác định a để A, B nằm về hai phía trục tung
Lời giải

Dạng 16. Ứng dụng hệ thức Viet trong giải toán hình học
Một trong những phương pháp giải toán hình học là “phương pháp đai số”, phương pháp được sử dụng hiệu quả trong một số dạng bài như: tính độ dài đoạn thẳng, một số bài toán cực trị hình học. Khi kết hợp với hệ thức Viet, ta sẽ có những lời giải hay và thú vị.
Ví dụ: Cho hình vuông ABCD có cạnh a và hai điểm M, N theo thứ tự chuyển động trên cạnh BC và CD sao cho góc MAN = 45 độ. Tìm GTNN và GTLN của diện tích ΔAMN.
Lời giải

Vừa rồi là bài viết các dạng bài hệ thức Viet có kèm ví dụ và lời giải cụ thể HOCMAI gửi đến bạn. Viet là hệ thức ứng dụng được trong rất nhiều dạng bài tập, vì vậy hãy tham khảo thật kỹ bài viết để phân biệt và sử dụng hợp lý hệ thực này để làm bài nhé!
















