Định lý Viet là một trong những kiến thức cơ bản nhưng cũng vô cùng quan trọng của chương trình toán Trung học cơ sở nói chung và trong chương trình Toán 9. Đây cũng là chuyên đề thường xuyên được ứng dụng trong các bài tập trong các kì thi học sinh giỏi, ôn thi tuyển sinh lớp 10 môn Toán. Chính vì vậy, bài viết này HOCMAI sẽ chia sẻ toàn bộ kiến thức cơ bản cần nhớ và các dạng bài tập về định lý Viet để các em học sinh có thể tham khảo!
A. Lý thuyết về định lý Viet
1. Định nghĩa
Cho cho một phương trình bậc 2 một ẩn có dạng:
ax² + bx + c = 0 (điều kiện: a≠0)
Khi phương trình trên có 2 nghiệm x1 và x2 thì 2 nghiệm của phương trình này thỏa mãn hệ thức sau:
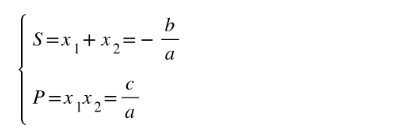
Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP
2. Hệ quả của định lý Viet:
Dựa vào hệ thức Viet ta có: Với một phương trình bậc 2 một ẩn có nghiệm, ta hoàn toàn có thể nhẩm nhanh trực tiếp nghiệm của phương trình bậc 2 một ẩn đã cho trong một số trường hợp sau:
- Nếu a+b+c=0 thì phương trình ax² + bx + c có 1 nghiệm x1 = 1 và x2 = c/a
- Nếu a-b+c=0 thì phương trình ax² + bx + c có 2 nghiệm x1 = -1 và x2 = -c/a
3. Định lý đảo của định lý Viet
Giả sử hai số thực x1 và x2 xác định thỏa mãn hệ thức sau:
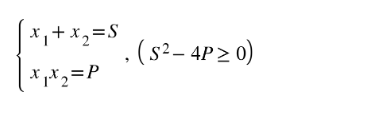
Thì 2 số thực x1 và x2 đã cho là 2 nghiệm của phương trình bậc 2 một ẩn có dạng:
x2 – Sx + P = 0
B. Các dạng bài tập ứng dụng định lý Viet
Dạng bài tập 1: Vận dụng hệ thức Viet đề hai số khi biết được tổng và tích.
Hướng dẫn giải
Nếu có 2 số u và v xác định thỏa mãn điều kiện

thì 2 số u, v sẽ là nghiệm của phương trình bậc 2 một ẩn có dạng: x² – Sx + P = 0.
Như vậy, thông qua việc xác định hai số u, v , các em học sinh sẽ quay về dạng bài toán giải phương trình bậc 2 có một ẩn:
- Nếu S2 – 4P ≥ 0 thì tồn tại u và v.
- Nếu S2 – 4P < 0 sẽ không tồn tại 2 số thỏa mãn yêu cầu
Dạng bài tập 2: Áp dụng định ý Viet để tính giá trị của biểu thức đối xứng
Hướng dẫn giải:
Các nhận biết biểu thức đối xứng: Một biểu thức là biểu thức đối xứng với 2 giá trị x1, x2 khi ta đổi chỗ x1, x2 cho nhau thì giá trị biểu thức không thay đổi:
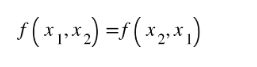
Nếu f là một biểu thức đối xứng thì biểu thức này sẽ luôn tồn tại các cách biểu diễn thông qua biểu thức đối xứng có ẩn là S=x1+x2 và P=x1x2
Một số cách biểu diễn S và P thường gặp là:
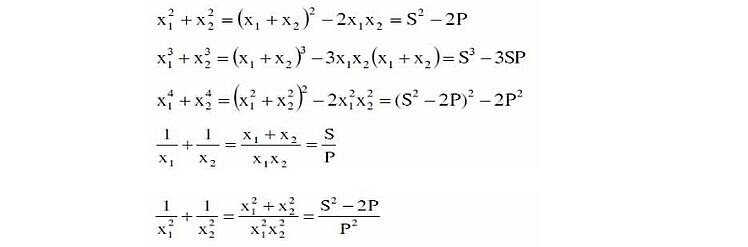
Sau đó, áp dụng định lý Viet, ta có ta tính được giá trị biểu thức cần tìm
Dạng bài tập 3: Áp dụng định lý Viet vào các dạng bài tập có chứa tham số
Đối với các bài tập thuộc dạng phương trình có chứa tham số, điều kiện đầu tiên là phải xét các trường hợp để phương trình bậc 2 tồn tại nghiệm. Sau đó áp dụng định lý Viet đã nói ở trên cho phương trình, ta sẽ có được các hệ thức của hai nghiệm x1, x2 theo tham số đã cho của đề bài, sau đó kết hợp với các dữ kiện đề bài đề tìm ra đáp án.
C. Bài tập thực hành về hệ thức Viet và ứng dụng
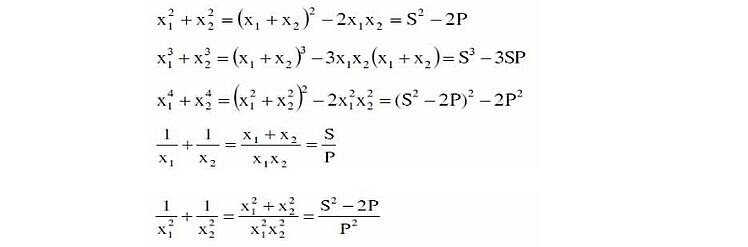


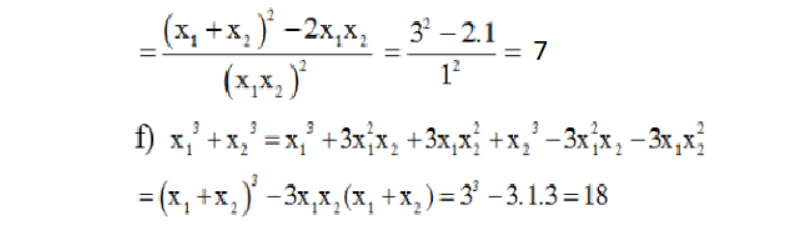

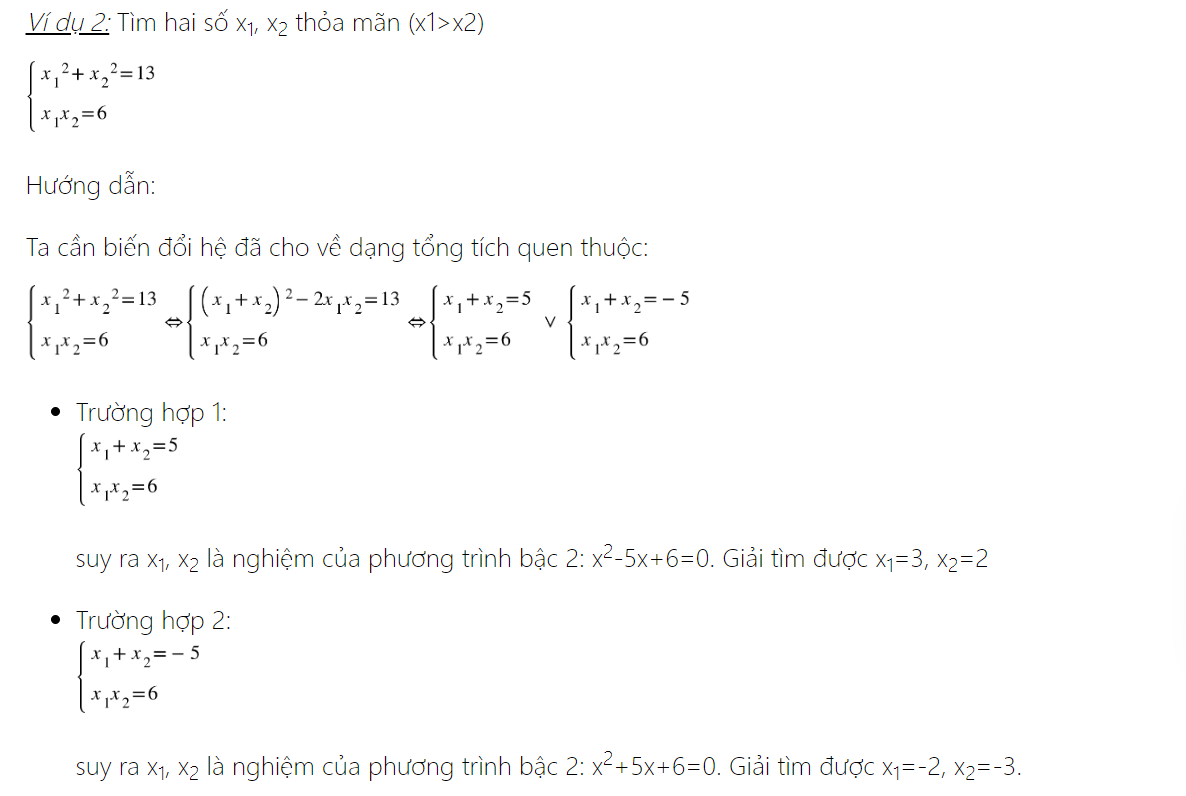


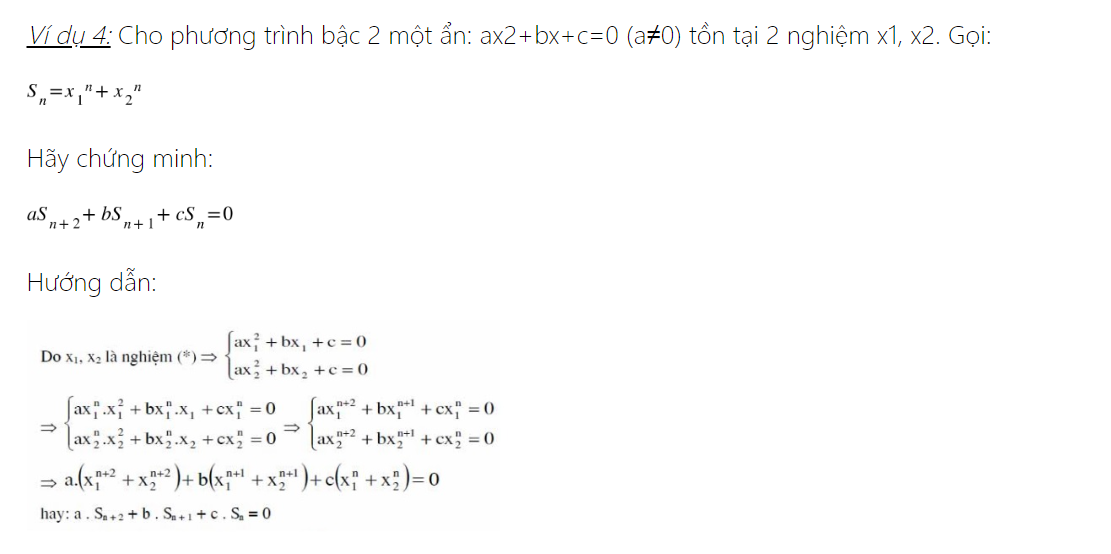




Tham khảo thêm:
















