A. Quy tắc giải hệ phương trình bằng phương pháp cộng đại số
Để áp dụng phương pháp cộng đại số khi giải hệ phương trình, các em học sinh thực hiện bằng các bước sau:
Bước 1: Cộng trừ các vế của hệ phương trình đã cho với cùng một số hoặc phương trình để ra một phương trình mới (phương trình mới có thể rút gọn hoặc các ẩn số được tối giản)
Bước 2: Thế phương trình mới sau khi được rút gọn vào 1 trong 2 phương trình và giữ nguyên phương trình còn lại rồi tiến hành giải hệ phương trình mới để tìm ra kết quả.
B. Các dạng bài thường gặp về giải hệ phương trình bằng phương pháp cộng đại số
Dạng bài tập 1: Sử dụng trực tiếp phương pháp cộng đại số
Phương pháp làm bài: Từ quy tắc cộng đại số, để giải hệ phương trình, các em học sinh cần làm các bước sau:
Bước 1: Nhân hoặc chia cả 2 vế của 1 trong 2 phương trình với một số thích hợp sao cho hệ số của một ẩn của 2 phương trình bằng nhau hoặc đối nhau
Bước 2: Tiến hành cộng (trong trường hợp 2 ẩn đối nhau) hoặc trừ (trong trường hợp 2 ẩn bằng nhau) để triệt tiêu 1 ẩn. Từ đó ta được một phương trình mới chỉ còn 1 ẩn duy nhất.
Bước 3: Tiến hành giải phương trình 1 ẩn. Sau đó thế kết quả vào 1 trong 2 phương trình đã cho để tìm ra ẩn còn lại
Dạng bài tập 2: Đưa hệ phương trình về dạng phương trình bậc nhất 2 ẩn
Bước 1: Biến đổi hệ phương trình đã cho ở đề bài về hệ dạng phương trình bậc nhất hai ẩn.
Bước 2: Tìm ra mối liên hệ giữa 2 ẩn của hệ phương trình thông qua phương trình bậc nhất 2 ẩn
Bước 3: Sử dụng phương pháp thế vào 1 trong 2 phương trình của hệ. Ta được một phương trình 1 ẩn mới
Bước 4: Tiến hành giải phương trình 1 ẩn. Sau đó thế kết quả vào 1 trong 2 phương trình đã cho để tìm ra ẩn còn lại
Dạng bài tập 3: Giải hệ phương trình bằng phương pháp đặt ẩn phụ
Bước 1: Biến đổi (nếu cần) để tìm biểu thức chung của các phương trình của hệ
Bước 2: Tiến hành đặt ẩn phụ của biểu thức chung để ra hệ phương trình bậc nhất 2 ẩn mới
Bước 3: Giải hệ phương trình bậc nhất mới thông qua các phương pháp đã nói ở trên để tìm ra giá trịnh của ẩn phụ
Bước 4: Tính đáp án của hệ phương trình thông qua ẩn phụ
Dạng 4: Tìm điều kiện của tham số để thỏa mãn yêu cầu cho trước
Để làm được dạng bài này, các em học sinh cần nhớ một số lưu ý sau:
%22%3E%20%3Cpath%20d%3D%22M685%201299l614-614q19-19%2019-45t-19-45l-102-102q-19-19-45-19t-45%2019L640%20960%20429%20749q-19-19-45-19t-45%2019L237%20851q-19%2019-19%2045t19%2045l358%20358q19%2019%2045%2019t45-19zm851-883v960q0%20119-84.5%20203.5T1248%201664H288q-119%200-203.5-84.5T0%201376V416q0-119%2084.5-203.5T288%20128h960q119%200%20203.5%2084.5T1536%20416z%22%3E%3C%2Fpath%3E%20%3C%2Fsvg%3E)
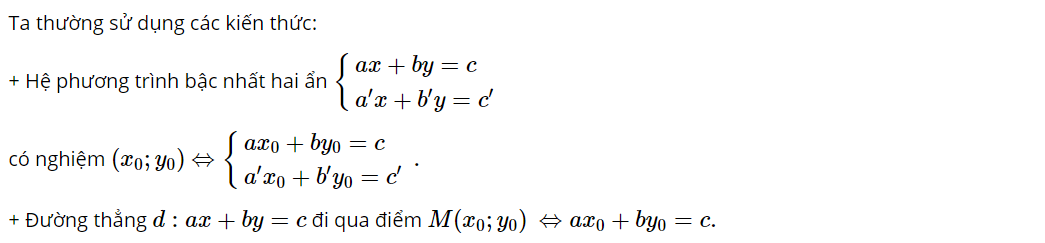
Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU- ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
- TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
- DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP
Ưu đãi đặt chỗ sớm - Giảm đến 45%! Áp dụng cho PHHS đăng ký trong tháng này!
C. Các bài tập thực hành
Bài tập cơ bản
Bài tập nâng cao
Trên đây là toàn bộ kiến thức cơ bản về giải hệ phương trình bằng phương pháp cộng đại số. Hy vọng bài viết này sẽ giúp các em học sinh có thêm kiến thức và phương pháp trong quá trình giải bài tập Toán lớp 9 hay trong quá trình ôn thi vào 10 môn Toán.
