Kỳ thi tuyển thi vào lớp 10 đang đến ngày một gần hơn. Đây cũng là khoảng thời gian mà các bạn học sinh cần tập trung phần lớn thời gian vào hoạt động ôn thi để cải thiện điểm số. Với môn Toán, một trong số những môn thi bắt buộc, HOCMAI sẽ đưa ra một vài gợi ý về phương pháp ôn thi vào lớp 10 cho những ai còn băn khoăn về cách học và luyện thi.
Phương pháp ôn thi Toán vào 10
Để quá trình ôn luyện trở nên hiệu quả hơn, các bạn học sinh cần có phương pháp ôn thi hợp lý nhất. Sau đây là những lời khuyên của thầy giáo Hồng Trí Quang – Giáo viên môn Toán tại Hệ thống Giáo dục HOCMAI muốn gửi đến các bạn học sinh trong những ngày thi cận kề này
Tập trung ôn phần kiến thức trọng tâm
Phần kiến thức trọng tâm là những kiến thức có trong cấu trúc đề thi. Những câu hỏi cơ bản từ câu 1 đến câu 3 phải đảm bảo nhuần nhuyễn, có thể vận dụng linh hoạt lý thuyết đã được học, tránh những lỗi sai nhỏ nhặt dẫn đến trừ điểm đáng tiếc trong bài thi.
Đối với những câu hỏi có chứa vận dụng cao như câu 4 và câu 5, các bạn học sinh nên dành nhiều thời gian để ôn tập hơn, không nên quá ép bản thân phải làm hết các phần ngoài khả năng của mình. Tập trung làm thật chậm và chắc các phần nằm trong khả năng của mình là quan trọng nhất.
Có mục tiêu và lộ trình rõ ràng
Ôn thi vào 10 là một hành trình dài và cần rất nhiều sự cố gắng và nỗ lực tự học từ các bạn học sinh. Theo đó, các bạn nên lập ra kế hoạch và có mục tiêu rõ ràng cho từng giai đoạn, ví dụ như giai đoạn ôn tập, giai đoạn luyện đề, giai đoạn cải thiện điểm.
Trong quá trình luyện đề, các bạn học sinh cũng cần lưu ý lựa chọn tài liệu phù hợp, cập nhật với xu hướng ra đề năm nay. Tài liệu nên có kèm lời giải, đáp án để dễ dàng đối chiếu, điều chỉnh cách làm sao cho đúng, hỗ trợ cho quá trình tự học trở nên hiệu quả hơn.

Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP
Kiến thức trọng tâm ôn thi vào lớp 10 môn Toán
Về kiến thức trọng tâm bao gồm ổng cộng 16 chuyên đề chính trải đều trong 2 phần đại số và hình học. Với những kiến thức này, các em học sinh không chỉ cần nắm vững lý thuyết, các kiến thức liên quan mà còn cần dành thời gian cho việc thực hành trực tiếp trên bài tập hoặc trên đề thi các năm. Điều này không chỉ giúp các em nắm chắc kiến thức một cách Logic mà còn luyện tập thói quyen cũng như phản xạ làm bài một cách nhanh chóng, tiết kiệm thời gian trong quá trình làm bài thi.
Các kiến thức trọng tâm ôn thi tốt nghiệp lớp 10 môn Toán bao gồm có:
Phần I: Chuyên đề Đại số
- Rút gọn và tính giá trị biểu thức
- Giải phương trình và hệ phương trình bậc nhất 2 ẩn
- Phương trình bậc 2 một ẩn
- Giải toán bằng cách lập phương trình hoặc hệ phương trình
- Hàm số và đồ thị
- Chứng minh bất đẳng thức
- Giải bất phương trình
- Tìm giá trị lớn nhất, nhỏ nhất của biểu thức
- Giải bài toán có nội dung số học
Phần II: Chuyên đề hình học
- Chứng minh các hệ thức hình học
- Chứng minh tứ giác nội tiếp và nhiều điểm cùng nằm trên đường tròn
- Chứng mình quan hệ tiếp xúc giữa đường thẳng và đường tròn hoặc 2 đường tròn
- Chứng minh các điểm cố định: xác định bao loại yếu tố
- Bài tập hình có nội dung tính toán
- Quỹ tích và dựng hình
- Bài toán về cực trị hình học
- Phần II: Chuyên đề Hình học
- Phần III: Đề thi tham khảo
- Phần IV: Lời giải và đáp số
Tìm hiểu thêm: 16 chuyên đề ôn thi vào 10 môn Toán
Nắm trọn kiến thức các môn ôn thi vào 10 đạt 9+ với bộ sách
Các dạng bài trọng tâm thường gặp ôn thi vào lớp 10 môn Toán
Dạng I: Rút gọn biểu thức có chứa căn thức bậc hai
Trong các dạng toán thi vào lớp 10, đây là dạng toán cơ bản các em học sinh đã được học trong chương trình Toán lớp 9. Đề làm được dạng này đòi hỏiu các em phải nắm chắc định nghĩa căn bậc hai số học và các quy tắc để biến đổi căn bậc hai. Để thuận tiện cho việc ôn tập, HOCMAI chia dạng này thành 2 loại bao gồm: biểu thức số học và biểu thức đại số.
1/ Biểu thức số học
Phương pháp làm bài:
Sử dụng các công thức biến đổi căn thức được học: đưa ra phân tích ; đưa vào ;khử căn thức; trục căn thức; cộng, trừ những căn thức đồng dạng; rút gọn phân số…) để rút gọn biểu thức một cách ngắn nhất.
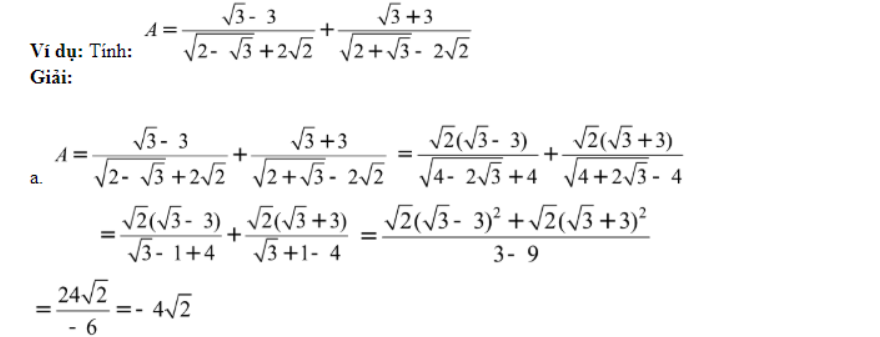
2/ Biểu thức đại số:
Phương pháp làm bài:
– Phân tích đa thức phân số với tử và mẫu thành nhân tử;
– Tìm điều kiện xác định đa thức
– Tiến hành rút gọn từng phân thức
– Sử dụng các phương pháp biến đổi đồng nhất như:
+ Quy đồng (sử dụng trong các dạng bài cộng trừ) ; nhân ,chia.
+ Bỏ ngoặc đơn, ngoặc kép: bằng cách nhân đơn hay đa thức hoặc sử dụng hằng đẳng thức đáng nhớ
+ Thu gọn: cộng, trừ các hạng tử đồng dạng.
+ Sử dụng phương pháp phân tích đa thức thành nhân tử

Dạng II: Đồ thị y = ax + b (a ≠ 0) và y = ax2 (a ≠ 0), tương quan giữa chúng
Trong các dạng trong đề thi toán vào lớp 10, để làm các dạng toán có liên quan tới đồ thị hàm số em học sinh bắt buộc phải nắm được định nghĩa và hình thái của các dạng đồ thị hàm bậc nhất (dạng đường thẳng), hàm bậc hai (parabol), hàm bậc 3 (dấu ngã) hay các dạng đồ thị đối xứng. Một số dạng bài về đồ thị bao gồm có:
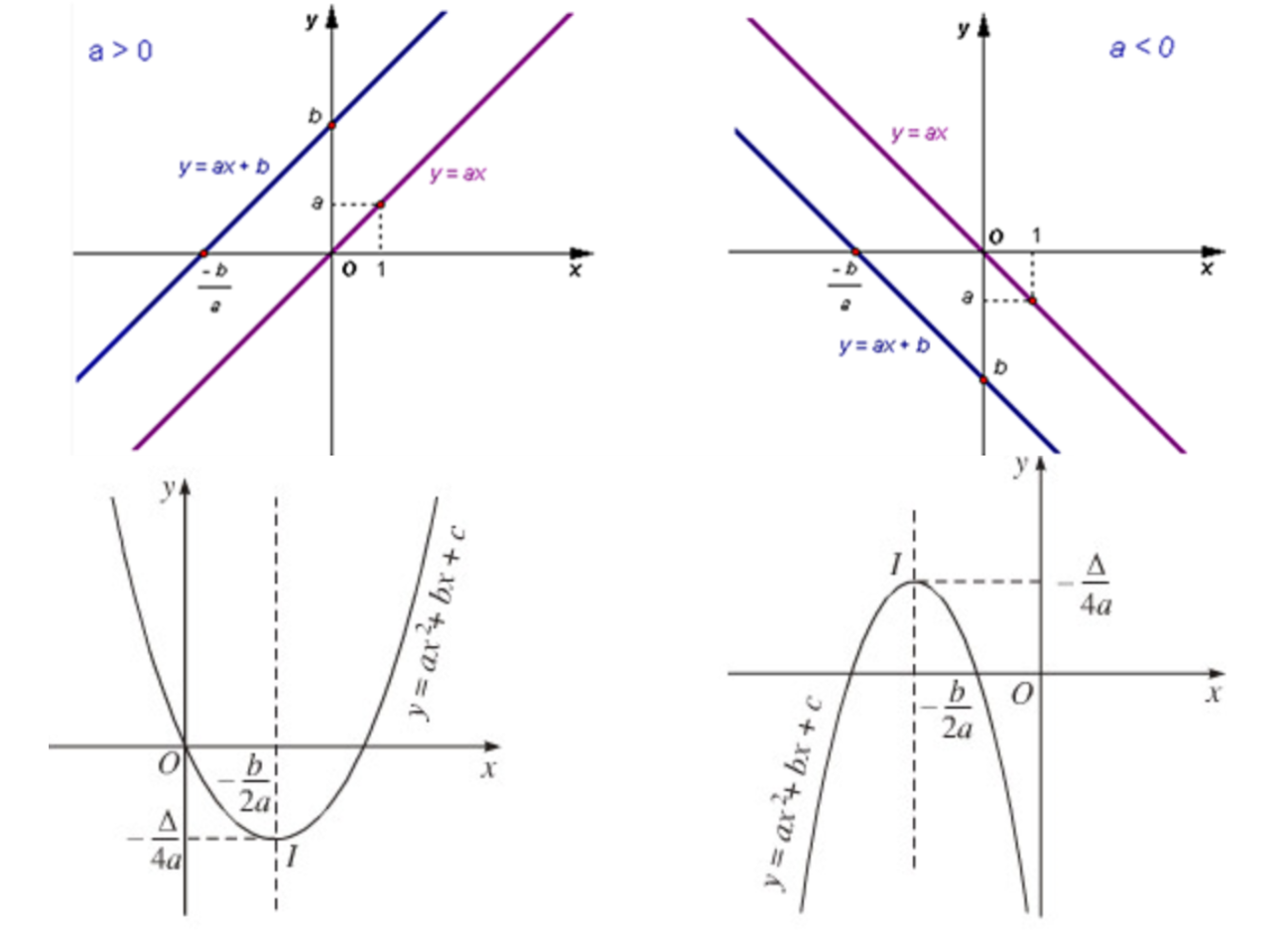
1. Điểm thuộc đường – đường đi qua điểm.
Phương pháp giải bài tập: Điểm A(xA; yA) thuộc đồ thị hàm số y = f(x) yA = f(xA).
VD: Tìm hệ số a của hàm số: y = ax2 biết đồ thị hàm số của nó đi qua điểm A(2;4)
Giải:
Do đồ thị hàm số đi qua điểm A(2;4) nên: 4 = a.22 ⇔ a = 1
2. Cách tìm giao điểm của hai đường y = f(x) và y = g(x).
Phương pháp giải bài tập: để làm được dạng bài này, các em học sinh thực hiện theo các bước sau:
Bước 1: Tìm hoành độ giao điểm: đây là nghiệm của phương trình f(x) = g(x) (*)
Bước 2: Sử dụng x đã tìm được tìm được thay vào 1 trong hai công thức y = f(x) hoặc y = g(x) để tìm tung độ giao nhau của 2 đồ thị đường thẳng
Lưu ý: Số nghiệm của phương trình (*) đã lập ở trên chính là số giao điểm giữa 2 đường thẳng y = f(x) và y = g(x)
3. Dạng bài tìm mối quan hệ giữa (d): y = ax + b và (P): y = a’x² (a’0).
3.1. Tìm tọa độ giao điểm của (d) và (P).
Phương pháp làm bài:
Bước 1: Tìm hoành độ giao điểm là nghiệm của pt:
a’x² = ax + b (#) ⇔ a’x² – ax – b = 0 (1)
Bước 2: Sử dụng nghiệm đã tìm thay vào hàm số y = ax +b hoặc y = ax² để xác định tung độ y của giao điểm.
Lưu ý: Số nghiệm của pt (1) đã tạo ở trên chính là số giao điểm của 2 đường thẳng (d) và (P).
3.2. Tìm điều kiện để (d) và (P) cắt; tiếp xúc; không cắt nhau:
Phương pháp làm bài:
Từ phương trình (#) ta xét các điều kiện để phương trình: ax² – ax – b = 0 có nghiệm, vô nghiệm. Xét Δ = (-a)² + 4ab
a) Nếu phương trình (d) và (P) cắt nhau ⇔ pt có hai nghiệm phân biệt ⇔ Δ > 0
b) Nếu phương trình (d) và (P) tiếp xúc với nhau ⇔ pt có nghiệm kép ⇔ Δ = 0
c) Nếu 2 phương trình (d) và (P) không giao nhau ⇔ pt vô nghiệm ⇔ Δ < 0
Nắm trọn mọi dạng đề thi vào 10 với khóa học HM10 Luyện đề
Dạng III: Hệ phương trình và phương trình
Giải hệ phương trình và phương trình là một trong những dạng toán cơ bản nhất trong các dạng bài xuất hiện trong đề thi vào lớp 10 môn Toán. Giải hệ phương trình sử dụng 2 phương pháp là cộng đại số hoặc thế, giải pt bậc hai ta sử dụng công thức nghiệm. bên cạnh đó, HOCMAI sẽ giới thiệu thêm một số dạng bài chứa tham số liên quan đến phương trình.
1. Hệ phương trình bậc nhất 2 ẩn
Phương pháp giải bài:
+ Dạng tổng quát:
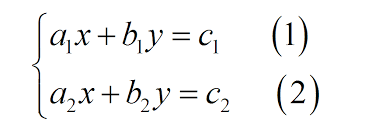
+ Cách giải: Để giải phương trình bậc nhất, ta chủ yếu sử dụng 2 phương pháp chủ yếu là
- Phương pháp thế.
- Phương pháp cộng đại số.
2. PT bậc hai + Hệ thức Vi-ét
2.1. Cách giải pt bậc hai có dạng: ax² + bx + c = 0 ( a ≠ 0)
Phương pháp làm bài:

2.2. Định lý Vi-ét:
Phương pháp làm các dạng bài liên quan tới định lý Vi-ét: Áp dụng các hệ quả sau
Nếu x1 và x2 là nghiệm của pt : ax² + bx + c = 0 (a ≠0) thì:
- S = x1 + x2 = -b/a
- p = x1x2 =c/a.
Và ngược lại: Nếu có hai số x1, x2 thỏa mãn điều kiện x1 + x2 = S và x1x2 = p thì hai số trên là nghiệm (nếu có) của pt bậc 2 có dạng: x² – Sx + P = 0
3. Tính giá trị của các biểu thức nghiệm:
Phương pháp làm bài: Biến đổi biểu thức đề bài ra để xuất hiện các biểu thức có dạng: (x1+x2) và x1x2
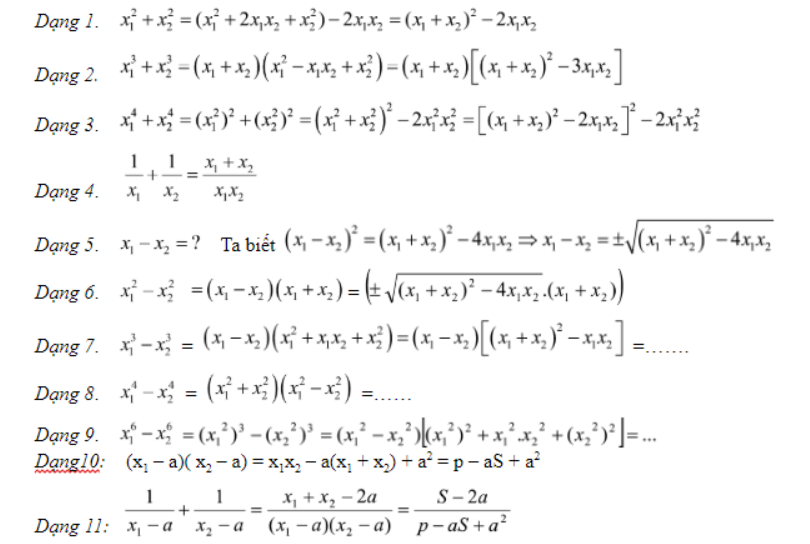
4. Tìm hệ thức liên hệ giữa hai nghiệm của phương trình sao cho nó không phụ thuộc vào tham số
Phương pháp làm bài:
Bước 1: Tìm điều kiện phương trình đã cho có hai nghiệm x1 và x2
(thường là a ≠ 0 và Δ ≥ 0)
Bước 2: Áp dụng hệ thức Vi-ét
Bước 3: Dựa vào hệ thức Vi-ét để rút biểu thức thành dạng tổng nghiệm hoặc tích nghiệm rồi sau đó đồng nhất các vế với nhau.
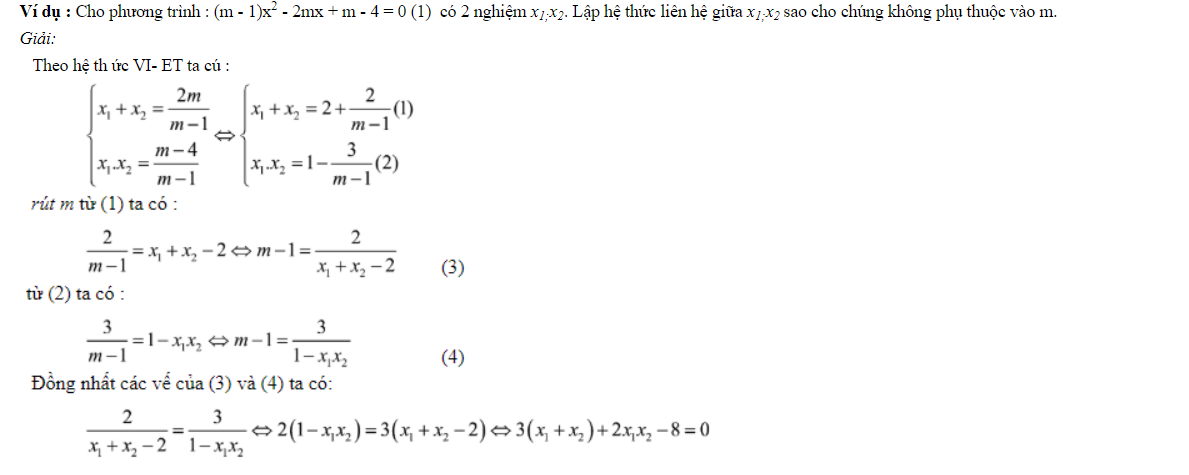
5. Tìm giá trị tham số của phương trình thỏa mãn biểu thức chứa nghiệm đã cho
Phương pháp giải bài tập:
– Tìm điều kiện để pt có hai nghiệm x1 và x2 (Điều kiện thường là a ≠ 0 và Δ ≥ 0)
– Từ biểu thức đã có, áp dụng hệ thức Vi-ét để giải phương trình
– Đối chiếu với tập xác định của điều kiện của tham số đã tìm trước đó để tìm ra đáp án.
Ví dụ minh họa:
Bài 1: Cho phương trình có dạng: x2 – 2(m + 3)x + m2 + 3 = 0
a) Giải pt khi m = -1 và m = 3
b) Tìm m để phương trình có một nghiệm x = 4
c) Tìm m để phương trình có hai nghiệm phân biệt với nhau
d) Tìm m để phương trình có hai nghiệm thoả mãn điều kiện x1 = x2
Bài 2: Cho phương trình có dạng : ( m + 1) x2 + 4mx + 4m – 1 = 0
a) Giải phương trình khi m = -2
b) Tìm m để phương trình có hai nghiệm phân biệt
c) Tìm m để phương trình có hai nghiệm thoã mãn điều kiện x1 = 2x2
Dạng IV: Giải bài toán bằng cách lập phương trình ôn thi tuyển sinh vào lớp 10 môn Toán
Trong các dạng bài xuất hiện trong đề thi toán vào lớp 10, đây là một trong các dạng toán rất được quan tâm trong thời gian gần đây vì dạng bài này có thể ứng dụng thực tế. Điều này đòi hỏi các em học sinh cần phải biết suy luận từ thực tế để đưa vào công thức toán.
Phương pháp giải bài tập dạng này:
Bước 1: Lập hệ phương trình hoặc phương trình dựa trên các dữ kiện có sẵn đề bài ra
- Chọn ẩn, đơn vị của ẩn, các điều kiện và tập xác định của ẩn đã đặt.
- Biểu đạt các đại lượng và dữ kiện khác dựa vào ẩn (lưu ý cần phải đồng nhất đơn vị).
- Dựa vào các dữ kiện, điều kiện của đề bài đã ra để tạo ra phương trình hoặc hệ phương trình.
Bước 2: Tiến hành giải hệ phương trình hoặc hệ phương trình đã tạo lập từ bước 1
Bước 3: Kết hợp với điều kiện hoặc tập xác định để đưa ra kết luận về nghiệm
Các công thức cơ bản cần nhớ đối trong quá trình giải các bài tập thuộc dạng bài vận dụng


Cấu trúc đề thi tuyển sinh vào lớp 10 môn Toán
Nắm chắc cấu trúc của đề thi là cách tốt nhất để các bạn học sinh đưa ra chiến thuật làm bài hợp lí, giúp tận dụng tối đa thời gian làm bài thi của mình. Với môn Toán, cấu trúc đề thi qua từng năm không có quá nhiều thay đổi và sự khác biệt giữa các tỉnh thành cũng không quá nhiều. Đề thi thường có 5 câu. Cụ thể:
Cấu trúc cơ bản của đề thi toán vào lớp 10
- Câu 1: Chiếm khoảng 20% tổng điểm. Đây là câu hỏi mang tính kiểm tra khả năng thông hiểu của học sinh về các dạng bài thuộc các chuyên đề như:
+ biểu thức,
+ phương trình,
+ bất phương trình,
+ tìm giá trị x để thỏa mãn yêu cầu,..
Lưu ý: Dạng bài về bất phương trình và tìm giá trị x để thỏa mãn đều là những dạng bài nâng cao và thường chiếm 0,5 điểm. - Câu 2: Chiếm khoảng 20% tổng điểm. Thường là các bài toán thực tế, vận dụng kiến thức về phương trình hoặc hệ phương trình để giải quyết bài tập. Câu 2 thường có thể sẽ bao gồm 2 yêu cầu nhỏ, thứ tự được xếp lần lượt theo độ khó tăng dần, từ thông hiểu đến vận dụng.
Lưu ý: Trong những năm gần đây, đề bài thuộc dạng này thường có 2 ý chính. Ý thứ nhất thuộc mức độ thông hiểu, bắt buộc các em học sinh cần phải nắm vững kiến thức mới có thể giải quyết được. Ý thứ hai nằm trong mức độ vận dụng thấp, không quá khó khăn đối các em học sinh. Tuy nhiên, các em học sinh cần phải đọc kỹ đề và cẩn thận vận dụng và kết hợp được các kiến thức để giải quyết bài toán.
- Câu 3: Chiếm khoảng 25% tổng điểm. Để làm được câu này, các bạn học sinh cần có đầy đủ kiến thức liên quan đến giải hệ phương trình, bài toán về đường thẳng, đồ thị, hệ thức Vi-et. Câu hỏi sẽ gồm nhiều ý nhỏ theo thứ tự từ dễ đến khó nhằm phân hóa năng lực của thí sinh.
- Câu 4: Chiếm khoảng 33% tổng điểm. Các kiến thức về hình học sẽ tập trung trong câu hỏi này. Bao gồm các phần nội dung liên quan đến chứng minh điểm, chứng minh tứ giác nội tiếp, tính góc, độ dài đoạn thẳng,… Các ý càng về cuối càng có mức độ phân hóa cao hơn. Các bạn học sinh lưu ý khi làm bài
- Câu 5: Chiếm khoảng 5% tổng điểm. Câu hỏi cuối sẽ cần học sinh tư duy nhiều hơn, nắm vững các kiến thức cơ bản là chưa đủ, cần vận dụng các kiến thức nâng cao để giải các dạng bài như chứng minh bất đẳng thức, tìm giá trị lớn nhất, nhỏ nhất,..Tuy nhiên câu hỏi này có giá trị điểm không cao nên các bạn thí sinh có thể lựa chọn làm hay không dựa theo khả năng.
Nắm trọn các dạng bài trong đề thi toán vào 10, tham khảo ngay:
Tổng quan về kiến thức:
Phần Đại số:
- Trong đề thi vào lớp 10 môn toán, phần đại số chiếm từ 6 đến 6,5 điểm. Trong đó, có khoảng từ 5 – 6,5 điểm đến từ những kiến thức cơ bản hoặc các câu hỏi ở mức độ vận dụng thấp giúp các em học sinh có thể dễ dàng “ăn điểm” trọn vẹn trong trường hợp làm tỉ mỉ, chi tiết và cẩn thận.
- Lời khuyên trong phần Đại số này là các em học sinh cần ôn tập một cách kĩ càng, hiểu bản chất của kiến thức để có thể nắm trọn điện tuyệt đối của phần này.
Phần Hình học:
- Phần hình học là phần các em học sinh cần đặc biệt lưu ý. Bên cạnh việc nắm chắc các kiến thức về hình học, các em cũng cần vẽ hình chính xác theo đúng yêu cầu bài toán vì nếu vẽ hình không chính xác, các em sẽ gặp phải rất nhiều khó khăn trong việc thực hiện các yêu cầu mà đề bài ra.
- Tận dụng và khai thác triệt để tất cả các tính chất của các dạng hình theo dữ kiện mà đề bài đã ra và cách chứng minh của từng loại theo yêu cầu. Khi thực hiện trọn vẹn các điều này thì khi gặp bất cứ các bài tập hình học nào, các em học sinh sẽ có nhiều ý tưởng và phương hướng giải quyết bài toán.
- Trong các bài toán về Toán hình học thường trong đề thi vào 10 môn toán có từ 3 đến 4 ý và được phân chia theo từng cấp độ và độ khó được nâng lên theo từng câu. Câu cuối cùng phần lớn luôn là câu khó nhất chỉ chiếm 0,5 điểm, còn các ý trên chủ yếu là những câu có giá trị 1 điểm.
Chi tiết về cấu trúc đề thi, các em học sinh có thể tham khảo bài viết: Cấu trúc đề thi vào 10 mới nhất
Bên cạnh đó, việc thực hành trực tiếp đề thi các năm là điều rất quan trọng để giúp các em học sinh có thể hiểu rõ nhất cấu trúc và ma trận đề thi, từ đó đưa ra lộ trình và phương pháp ôn thi phù hợp nhất dành cho bản thân. Các em học sinh có thể tham khảo trọn bộ tài liệu: Đề thi tuyển sinh lớp 10 môn Toán được HOCMAI sưu tầm để thực hành và đánh giá hệ thống kiến thức mà các em đã ôn tập.
Bài viết trên đã cung cấp cho các bạn những thông tin liên quan đến ôn thi vào 10 làm sao cho hiệu quả. Hy vọng những chia sẻ trên từ HOCMAI đã phần nào giúp các bạn học sinh có thêm tinh thần và năng lượng để chuẩn bị sẵn sàng cho kỳ thi tuyển sinh lớp 10 năm 2022. Chúc các bạn thành công!
Tham khảo thêm:


















