Hình cầu là một hình dạng được ứng dụng phổ biến trong đời sống thường ngày. Bạn có thể bắt gặp hình cầu qua hình dạng của quả bóng bàn, viên bi, quả địa cầu,… Trong bài viết này, HOCMAI sẽ giới thiệu đến các bạn học sinh những kiến thức về hình cầu trong toán học.
I. Khái niệm hình cầu
1. Hình cầu là gì?
Hình cầu là hình được tạo ra khi ta xoay nửa hình tròn một vòng quanh đường kính của hình tròn.
Khi xoay nửa hình tròn tâm O, bán kính R một vòng quanh trục (đường kính) AB cố định trong không gian ba chiều. Ta sẽ tạo thành một hình cầu.
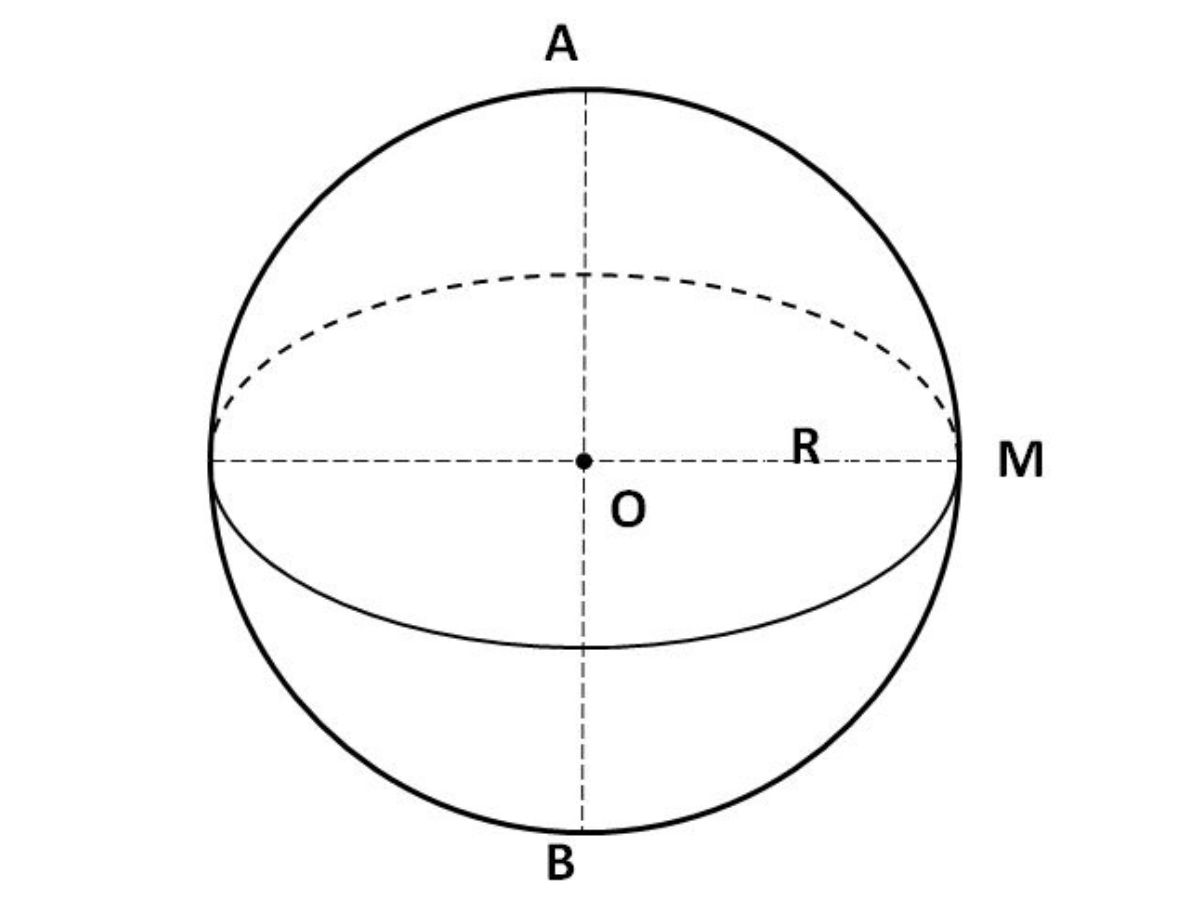
Khi đó O được gọi tâm hình cầu, R là bán kính của hình cầu hay mặt cầu đó.
2. Mặt cầu là gì?
Tập hợp các điểm cách đều tâm O với khoảng cách không đổi bằng R (bán kính) được gọi là mặt cầu.
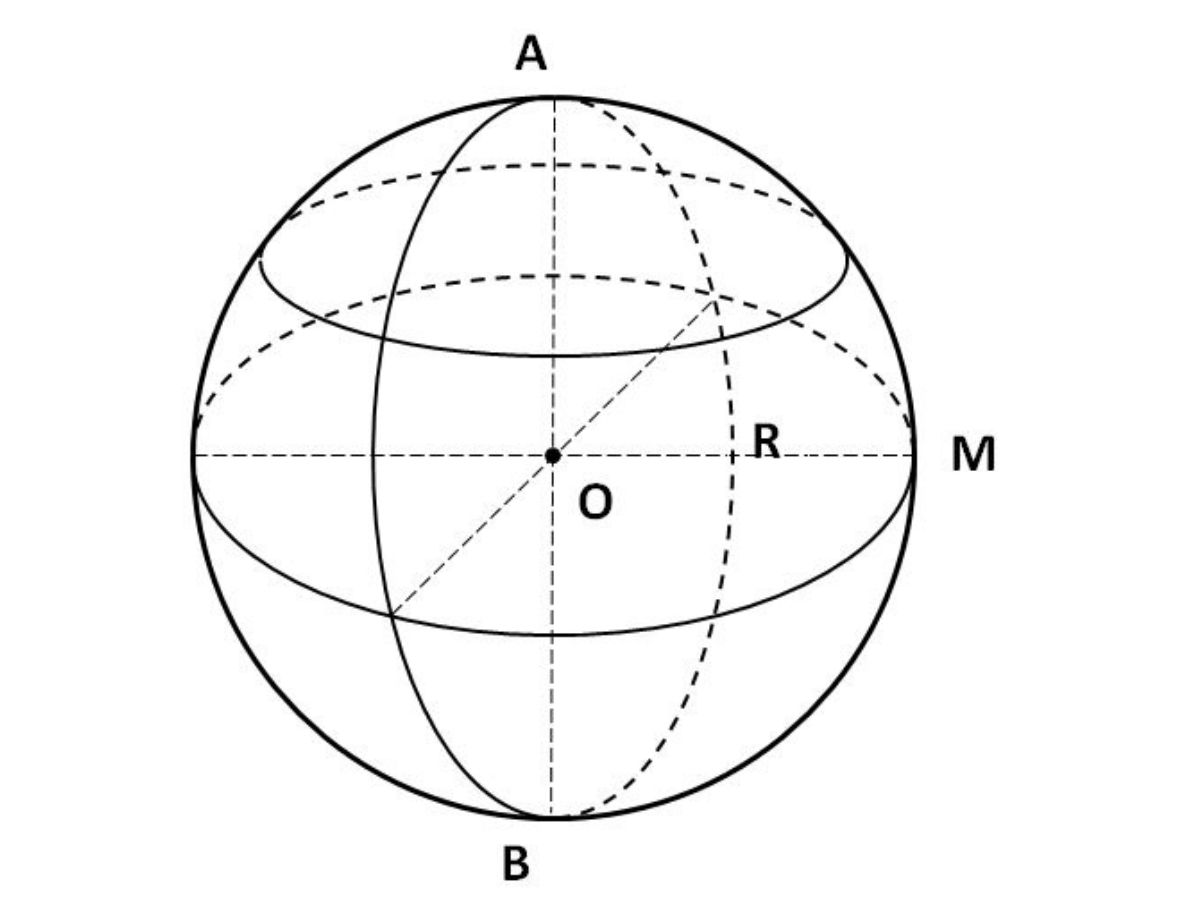
Khi ta cắt mặt cầu bởi một mặt phẳng, mặt cắt trong hình cầu đó luôn luôn là một hình tròn. Có 2 trường hợp:
- Nếu mặt phẳng cắt mặt cầu đi qua tâm O thì đường tròn có bán kính bằng R. Đây được gọi là đường tròn lớn.
- Nếu mặt phẳng cắt mặt cầu không đi qua tâm O thì đường tròn có bán kính bé hơn R. Đây được gọi là đường tròn nhỏ.
3. Tính chất của hình cầu
Hình cầu có 2 tính chất chính:
- Bất kể đường thẳng nào đi qua tâm của nó là trục đối xứng và giao với hình cầu. Khi ta xoay một quả cầu quanh trục này ở bất cứ góc độ nào, nó sẽ vẫn biến thành chính nó.
- Mặt phẳng cắt hình hình cầu qua tâm sẽ chia hình cầu đó thành hai phần bằng nhau. Được gọi là mặt phẳng phản xạ.
II. Công thức và cách tính diện tích hình cầu
Diện tích xung quanh hay diện tích hình cầu chính là diện tích mặt cầu bên trong hình cầu.
1. Công thức tính diện tích hình cầu:
Được tính theo công thức:
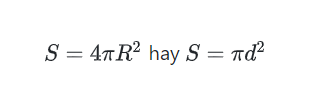
Trong đó:
- S là diện tích hình cầu
- π là hằng số Pi, với Pi xấp xỉ bằng 3,14
- R là bán kính hình cầu
- d là đường kính hình cầu
2. Ví dụ về bài tập tính toán diện tích hình cầu
Bài tập ví dụ 1: Cho một hình cầu có bán kính R = 6cm. Tính diện tích của mặt cầu?
Hướng dẫn giải
Theo đề bài, ta đã có bán kính của hình cầu là 6cm. Áp dụng theo công thức tính diện tích hình cầu ở trên. Ta có:
Diện tích hình cầu: S = 4 x π x R^2= 4 x π x 6^2 = ~ 452 (cm2)
Bài tập ví dụ 2: Cho một hình cầu có đường kính d = 6cm. Tính diện tích của mặt cầu?
Theo đề bài, ta đã có đường kính của hình cầu là 6cm. Áp dụng theo công thức tính diện tích hình cầu ở trên. Ta có:
Diện tích hình cầu: S = π x d^2 = π x 6^2 = ~ 114 (cm2)
III. Công thức và cách tính thể tích hình cầu
Lượng không gian mà hình cầu chiếm chính là thể tích của hình cầu. Để tính được thể tích hình cầu, chúng ta cần sử dụng đơn vị đo lập phương của khoảng cách (mũ 3).
1. Công thức tính thể tích hình cầu
Để biết được cách tính thể tích hình cầu, các bạn học sinh cùng tham khảo qua hình ảnh sau đây:
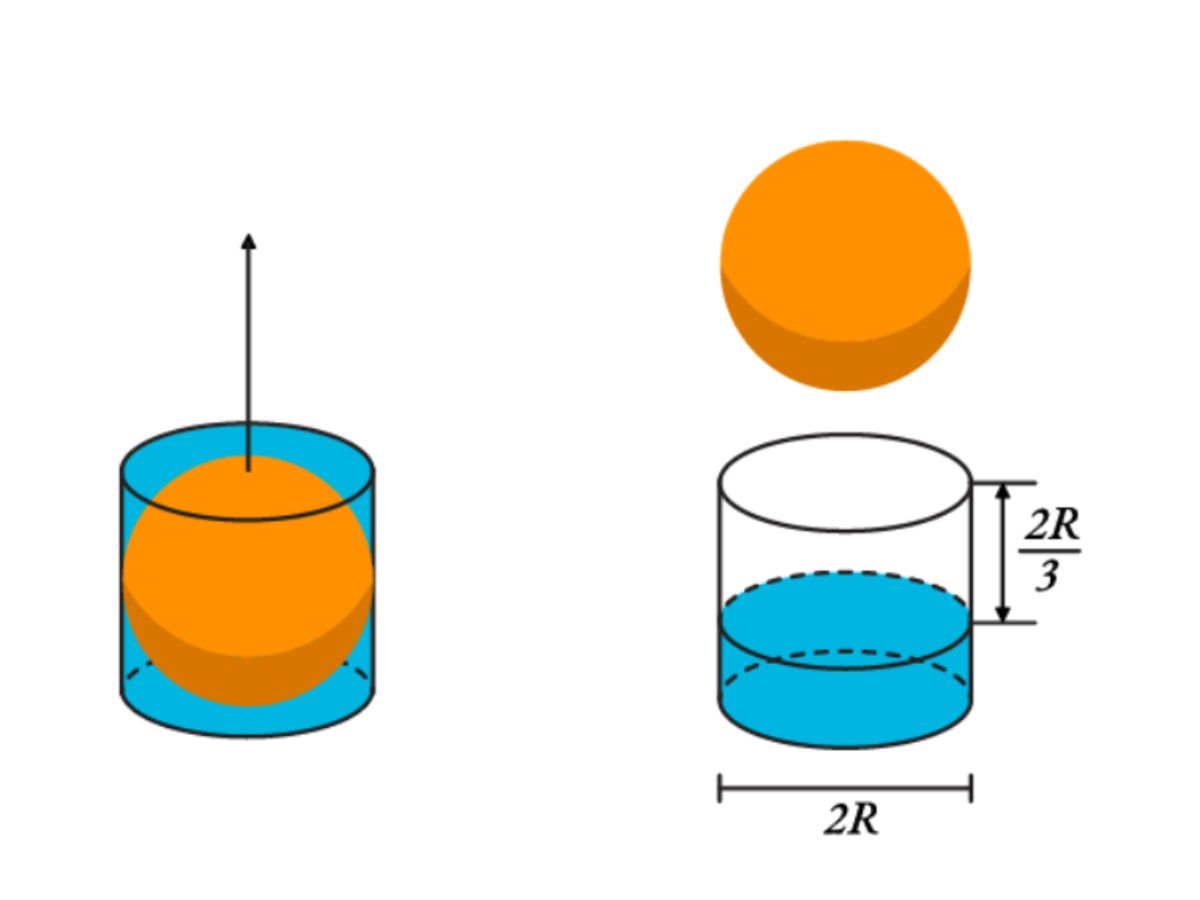
Hình ảnh trên chúng ta thấy được một quả bóng bán hình cầu có bán kính R và một cốc nước hình trụ có kích thước như trên. Trong đó:
- Hình quả bóng nằm gọn trong cốc nước
- Khi đưa quả bóng ra khỏi mặt nước, ta thấy lượng nước bị giảm đi một khoảng chính xác bằng 1/3 hình trụ.
Từ đó suy ra, thể tích của hình cầu bằng 2/3 thể tích của hình trụ. Cụ thể:
V = 4/3πR^3
Trong đó:
- V là thể tích hình cầu
- π là hằng số Pi, với Pi xấp xỉ bằng 3,14
- R là bán kính hình cầu
2. Ví dụ về bài tập tính toán diện tích hình cầu
Bài tập: Cho hình tròn A có chu vi là 30 cm. Tìm thể tích hình cầu có bán kính bằng bán kính của hình tròn vừa cho.
Hướng dẫn giải
Để tìm được thể tích của hình nón này, đầu tiên ta cần tìm bán kính r của hình tròn có chu vi = 30cm.
Chu vi hình tròn A = 2π x r = 30 cm => Bán kính r = C/2π = ~ 4,8 cm
Thể tích hình cầu cần tìm là: V = 4/3π x r^3 = 4/3π x 4,8^3 = ~ 463 (cm3)
Bài viết liên quan:
Vừa rồi là bài viết chia sẻ những thông tin và các công thức tính liên quan của hình cầu. Qua bài viết, mong rằng các bạn có thể dễ dàng tiếp thu và ứng dụng để giải các bài tập. Nếu bạn đang có thắc mắc hoặc vấn đề gì cần giải đáp, hãy để lại bình luận ở cuối bài viết. Cảm ơn bạn đã theo dõi bài viết, hẹn gặp lại các bạn ở các bài viết sau tại hoctot.hocmai.vn.

















