Hình nón là là một hình đặc biệt trong hình học không gian. Bài viết dưới đây của HOCMAI sẽ chia sẻ đến bạn những kiến thức thú vị về hình nón cũng như hướng dẫn cụ thể cách giải các dạng bài tập như tính diện tích, thể tích của hình nón.
I. Khái niệm hình nón
Trong Toán học, hình nón là một dạng hình học không gian ba chiều đặc biệt. Hình học này có 1 bề mặt phẳng gọi là đáy và 1 bề mặt cong hướng lên phía trên được gọi là đỉnh.
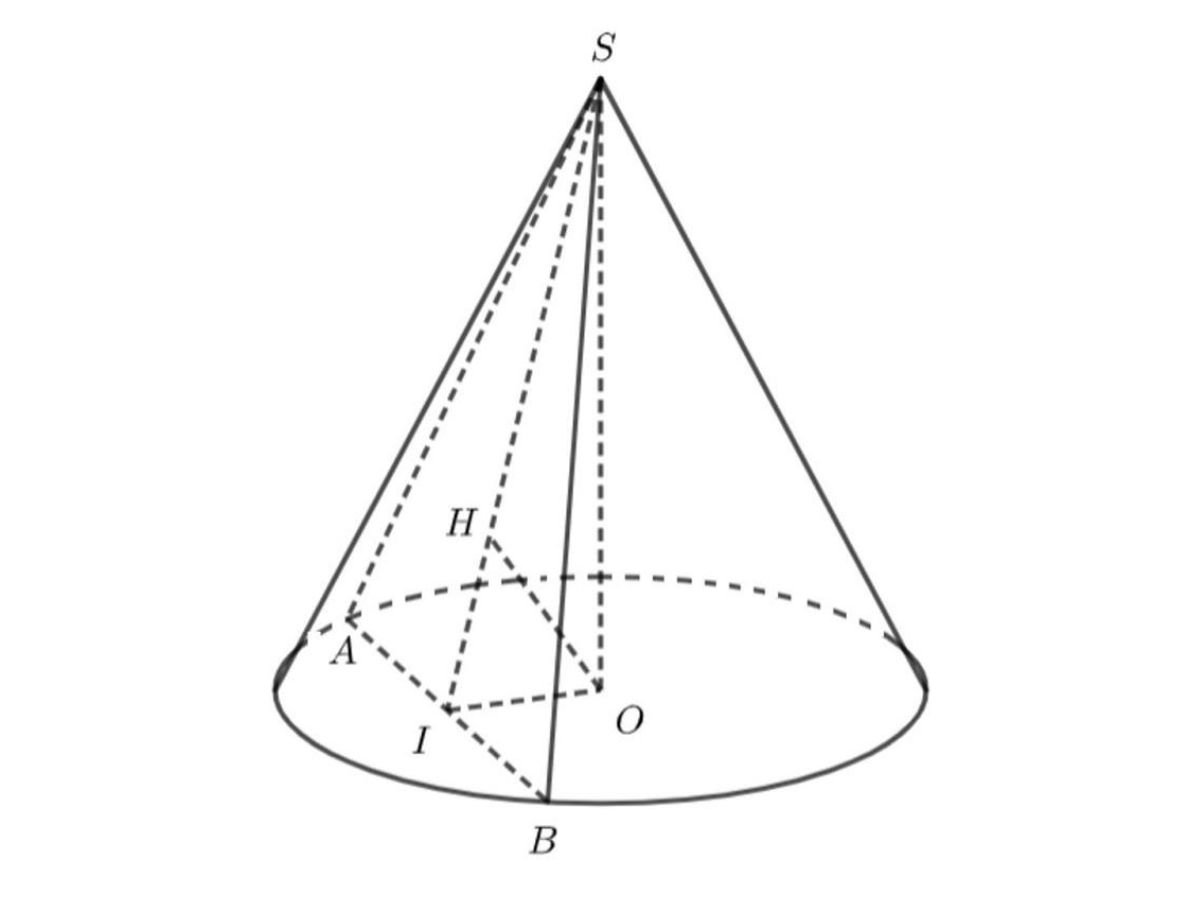
Trong đời sống hằng ngày, các bạn học sinh có thể bắt gặp các ứng dụng có thiết kế hình nón như nón lá, mũ sinh nhật, đế của cây kem ốc quế,…
Tính chất của hình nón
Bạn có thể dễ dàng nhận biết hình nón qua một số tính chất của nó. Bao gồm:
- Hình có một đỉnh là hình tam giác.
- Đáy hình nón là hình tròn.
- Hình nón là hình đặc biệt không hề có bất cứ cạnh nào.
- Khoảng cách tính từ tâm của vòng tròn đáy đến đỉnh được gọi là chiều cao (h) của hình nón. Trong hình nón, hình tạo bởi bán kính đáy và đường cao là một tam giác vuông.
Các loại hình nón thường gặp
Căn cứ vào hình dạng và vị trí của đỉnh nón, hình nón sẽ bao gồm những loại sau:
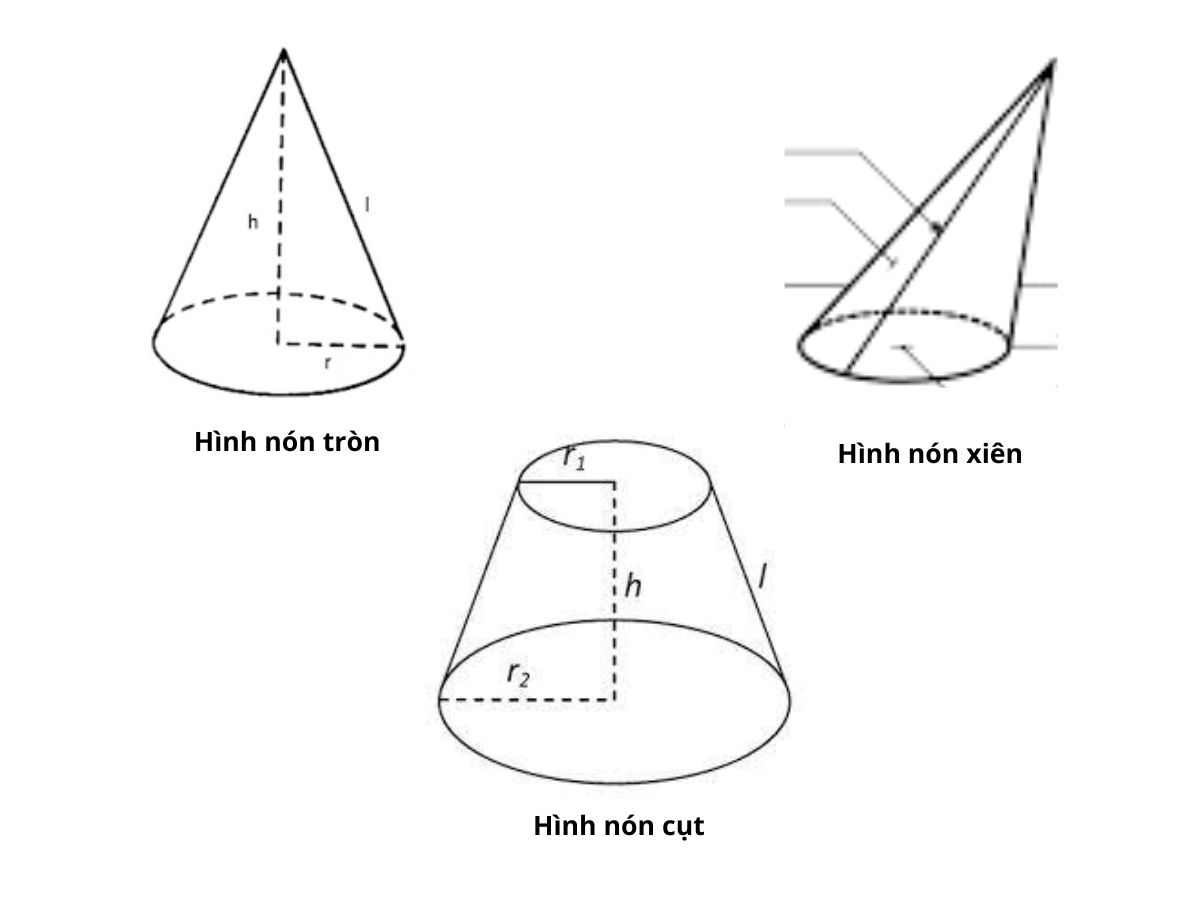
- Hình nón tròn: Là kiểu hình nón có đỉnh nằm thẳng lên và vuông góc với mặt đáy.
- Hình nón xiên: Là kiểu hình nón có đỉnh nằm xiên và không vuông góc với mặt đáy.
- Hình nón cụt: Là kiểu hình nón bị cắt mất phần đỉnh. Giống như khi hình nón bị cắt bởi một mặt phẳng song song với đáy, phần mặt phẳng nằm trong hình nón sẽ là một hình tròn. Hình tính từ đáy và mặt phẳng hình tròn này được gọi là hình nón cụt.
II. Cách xác định đường sinh, đường cao và bán kính đáy của hình nón
Để xác định được đường cao, đường sinh và bán kính đáy của hình nón. Các bạn phải hiểu được bản chất của các đường này. Cụ thể:
- Khoảng cách tính từ tâm của vòng tròn đáy đến đỉnh được gọi là đường cao (h) của hình nón.
- Khoảng cách tính từ đỉnh nối với một điểm bất kỳ trên đường tròn đáy được gọi là đường sinh (l) của hình nón.
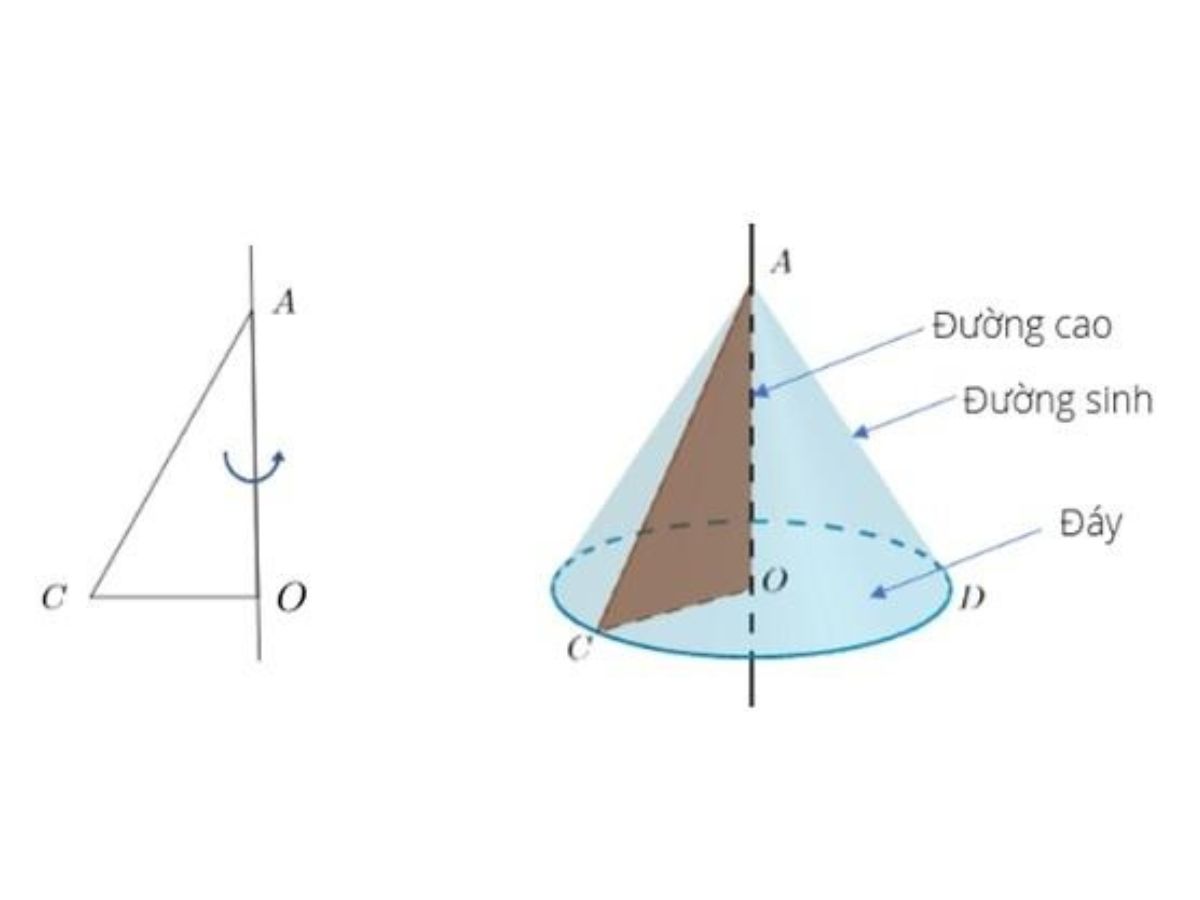
Trong hình nón, hình tạo bởi bán kính đáy và đường cao là một tam giác vuông – Trên ví dụ là tam giác AOC. Vậy nên đường cao (h) và bán kính đáy (r) sẽ là 2 cạnh góc vuông, đường sinh (l) chính là cạnh huyền.
Dựa vào điều này, chỉ cần đề bài cho kích thước của 2 trong 3 kích thước này. Bạn sẽ tính được độ dài của đường còn lại thông qua định lý Pytago. Cụ thể:

Công thức tính diện tích hình nón
Diện tích hình nón bao gồm diện tích xung quanh và diện tích toàn phần của nó. Công thức và cách tính cụ thể sẽ được HOCMAI gửi đến bạn ngay sau đây:
Diện tích xung quanh hình nón
Diện tích xung quanh hình nón chỉ bao gồm diện tích mặt bao quanh hình nón, không bao gồm diện tích mặt đáy.
Công thức tính diện tích xung quanh hình tròn cụ thể như sau:
Sxq = π.r.l
Trong đó:
- Sxq là diện tích xung quanh hình nón
- π là hằng số Pi, với Pi xấp xỉ bằng 3,14
- r là bán kính đáy hình nón
- l là đường sinh hình nón (SB trong hình minh họa là đường sinh)
Diện tích toàn phần hình nón
Diện tích toàn phần hình nón được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích hai đáy tròn.
Diện tích toàn phần được tính là độ lớn của toàn bộ không gian hình nón chiếm giữ, bao gồm diện tích đáy tròn và diện tích xung quanh của nó.
Vậy nên để tính diện tích toàn phần của hình nón, chúng ta sẽ tính tổng diện tích xung quanh và diện tích của đáy. Cụ thể như sau:
Stp = Sxq + Sđ = π.r.l + π.r^2
Trong đó:
- Stp là diện tích toàn phần
- Sxq là diện tích xung quanh
- Sđ là diện tích đáy
- π là hằng số Pi, với Pi xấp xỉ bằng 3,14
- r là bán kính đáy hình nón
- l là đường sinh hình nón
Bài tập ví dụ về tính toán diện tích hình trụ
Cho một hình nón có h = 5cm và r = 3cm. Hãy tính Sxq và Stp của hình nón?
Hướng dẫn giải
Để tính được Sxq và Stp , đầu tiên bạn phải tìm được độ dài đường sinh của hình nón. Theo đề bài, ta đã có chiều cao và bán kính đáy của hình nón. Áp dụng theo định lý PYtago ta sẽ tính được độ dài đường sinh của hình nón:
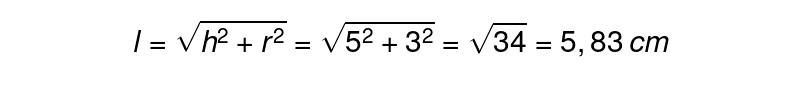
Sau khi đã có độ dài của đường sinh, việc còn lại của chúng ta là áp dụng công thức để tính Sxq và Stp của hình nón:
Diện tích xung quanh nón là:
Sxq = π.r.l = π x 3 x 5,83 = ~ 55 (cm2)
Diện tích toàn phần hình nón là:
Stp = π.r.l + π.r^2 = π x 3 x 5,83 + π x 3^2 = ~ 83 (cm2)
III. Thể tích và công thức tính thể tích hình nón
Thể tích của hình nón là lượng không gian mà hình nón ấy chiếm. Để tính được thể tích hình nón, bạn cần sử dụng đơn vị đo lập phương của khoảng cách (mũ 3 khoảng cách).
Công thức tính thể tích hình nón
Thể tích hình nón sẽ bằng tích của một phần ba diện tích mặt đáy với chiều cao. Cụ thể:
V= 1/3.π.r^2.h
Trong đó:
- V là thể tích hình nón
- π là hằng số Pi, với Pi xấp xỉ bằng 3,14
- r là bán kính đáy hình nón
- h là đường cao hình nón
Ví dụ về tính toán thể tích hình trụ
Cho một hình nón có h = 5cm và r = 3cm. Hãy tính thể tích của hình nón?
Hướng dẫn giải
Theo đề bài, ta đã có chiều cao và bán kính đáy của hình nón. Áp dụng theo công thức tính thể tích hình nón ở trên. Ta có:
Thể tích hình nón là: V= 1/3.π.r^2.h = 1/3 x π x 3^2 x 5 = 47 (cm3)
Tham khảo thêm một số bài viết:
- Hình trụ là gì?
- Cách tính diện tích hình tròn, chu vi hình tròn
- Diện tích hình bình hành, chu vi hình bình hành
- Cách tính diện tích hình thang, chu vi hình thang
Vừa rồi là bài viết về hình nón và các kiến thức thú vị về hình học đặc biệt này. Mong rằng những chia sẻ này sẽ giúp các bạn học sinh hiểu rõ về hình nón và biết cách áp dụng các công thức để giải các bài toán liên quan. Cảm ơn bạn đã theo dõi bài viết, hẹn gặp lại các bạn ở các bài viết sau tại hoctot.hocmai.vn.

















