Kỳ thi giữa kì sắp tới rồi các em học sinh thân mến. HOCMAI biết rằng mỗi mùa ôn thi đều khiến các em cảm thấy vô cùng áp lực. Bài viết Ôn thi giữa học kì 2 toán lớp 9 dưới đây được HOCMAI biên soạn nhằm trợ giúp cho các em trong quá trình ôn thi. Các em tham khảo bài viết nhé!
A. KIẾN THỨC TRỌNG TÂM ÔN THI GIỮA HỌC KÌ 2 TOÁN 9
I. Đại số – Ôn thi giữa học kì 2 toán lớp 9
1. Phương trình bậc nhất hai ẩn
– Phương trình bậc nhất hai ẩn là phương trình ở dạng ax + by = c. Trong đó: a,b,c là các số cho trước, a và b không đồng thời có giá trị bằng 0, x và y là hai ẩn số.
– Phương trình bậc nhất hai ẩn thì luôn có vô số nghiệm. Tập nghiệm của một phương trình ax + by = c được biểu diễn bởi đường thẳng (d): ax + by = c trên mặt phẳng tọa độ.
2. Hệ phương trình bậc nhất hai ẩn
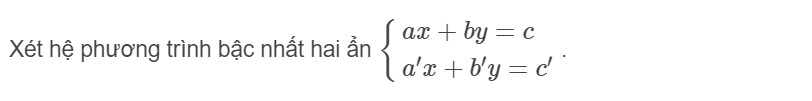
a) Số nghiệm của một hệ phương trình bậc nhất hai ẩn
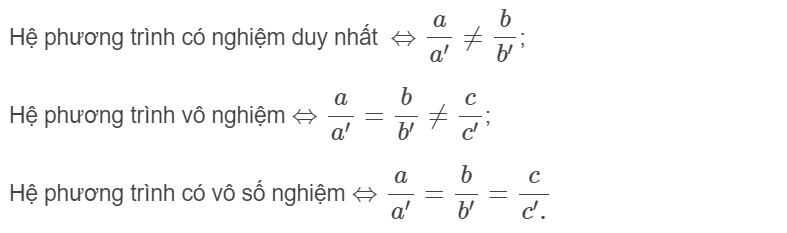
b) Cách giải một hệ phương trình bậc nhất hai ẩn
Cách 1: Phương pháp thế
Để giải được một hệ phương trình, ta biến đổi hệ phương trình đã cho thành một hệ tương đương đơn giản hơn. Phương pháp thế là một trong những cách thức biến đổi tương đương một hệ phương trình, quy tắc thế bao gồm 2 bước như sau:
Bước 1: Từ một phương trình nằm trong hệ phương trình đã cho (phương trình thứ nhất), ta biểu diễn một ẩn y theo ẩn x kia rồi thế vào phương trình thứ hai để ra một phương trình mới (chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế phương trình thứ hai ở trong hệ phương trình và vẫn giữ nguyên phương trình thứ nhất, ta được một hệ phương trình mới tương đương hệ phương trình đã cho.
Cách 2: Phương pháp cộng đại số
Để giải được hệ phương trình bậc nhất hai ẩn bằng phương pháp cộng đại số, ta sẽ sử dụng phương pháp cộng đại số, gồm có hai bước sau đây:
Bước 1: Cộng hoặc trừ từng vế của hai phương trình trong hệ phương trình đã cho để ra được một phương trình mới.
Bước 2: Dùng phương trình mới ấy thay thế cho một phương trình trong hệ phương trình và giữ nguyên phương trình kia, từ đó ta được một hệ mới tương đương với hệ đã cho.
3. Hệ phương trình chứa tham số
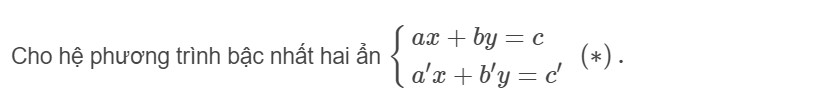
Cách 1: Để giải được hệ phương trình (*), ta thường sử dụng phương pháp cộng đại số hoặc phương pháp thế.
Cách 2: Từ hai phương trình trong hệ phương trình (*), sau khi dùng phương pháp cộng đại số hoặc phương pháp thế, ta đã thu được một phương trình mới (một ẩn). Khi đó số lượng nghiệm của phương trình mới bằng số lượng nghiệm của phương trình đã cho.
4. Giải bài toán bằng cách lập hệ phương trình
Các bước để giải bài toán bằng cách lập hệ phương trình:
Bước 1: Lập hệ phương trình:
– Chọn hai ẩn sau đó đặt điều kiện thích hợp cho chúng.
– Biểu diễn các đại lượng chưa biết dựa theo các ẩn và các đại lượng đã cho trước.
– Tạo lập hai phương trình biểu thị mối quan hệ giữa những đại lượng.
Bước 2: Giải hệ hai phương trình trên.
Bước 3: Trả lời: kiểm tra xem trong những nghiệm của hệ phương trình, nghiệm nào thì thích hợp với bài toán và kết luận.
II. Đề cương ôn thi giữa học kì 2 toán 9 phần Hình học
1. Góc ở tâm
Định nghĩa góc ở tâm
Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn.
Ví dụ: Trong hình dưới đây, có góc AOB là góc ở tâm (của đường tròn tâm O)
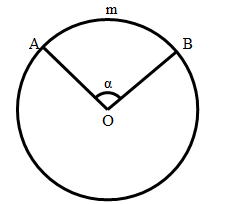
Số đo cung
– Số đo của cung nhỏ và số đo của góc ở tâm chắn cung đó bằng với nhau.
Ví dụ: Ở hình trên, ta có góc AOB bằng số đo cung AB, nghĩa là m = α.
– Số đo của cung lớn được tính bằng phép hiệu, lấy 360º trừ đi số đo của cung nhỏ (có chung 2 mút với cung lớn) thì ta có số đo của cung lớn.
– Số đo của nửa đường tròn là bằng 180º. Cả đường tròn có số đo bằng 360º. Cung không có số đo bằng 0º (cung có 2 mút trùng nhau).
So sánh hai cung
Trong cùng một đường tròn hoặc trong hai đường tròn bằng nhau:
– Hai cung được gọi là bằng nhau khi và chỉ khi chúng có số đo bằng nhau.
– Trong hai cung, cung mà có số đo lớn hơn thì được gọi là cung lớn hơn.
Định lý
Nếu điểm C nằm trên cung AB thì số đo cung AB bằng tổng số đo cung AC với số đo cung BC.
2. Liên hệ giữa dây và cung
Định lý 1:
Với hai cung nhỏ trong cùng một đường tròn hay trong hai đường tròn có số đo bằng nhau:
+) Hai cung bằng nhau thì căng hai dây bằng nhau.
+) Hai dây bằng nhau thì căng hai cung bằng nhau.
Định lý 2:
Với hai cung nhỏ trong cùng một đường tròn hay trong hai đường tròn có số đo bằng nhau:
+) Cung lớn hơn thì căng dây lớn hơn.
+) Dây lớn hơn thì căng cung lớn hơn.
Chú ý
+) Trong một đường tròn, hai cung bị chắn ở giữa hai dây song song thì có số đo bằng nhau.
+) Trong một đường tròn, đường kính mà đi qua điểm nằm chính giữa của một cung thì sẽ đi qua trung điểm của dây căng cung đó.
+) Trong một đường tròn, đường kính mà đi qua trung điểm của một dây (không qua tâm) thì sẽ đi qua điểm chính giữa của cung bị căng bởi dây đó.
+) Trong một đường tròn, đường kính mà đi qua điểm chính giữa của một cung thì sẽ vuông góc với dây căng cung đó và ngược lại.
3. Góc nội tiếp
Định nghĩa:
– Góc nội tiếp là góc mà có đỉnh nằm trên đường tròn và hai cạnh của góc chứa hai dây cung của đường tròn ấy.
– Cung nằm ở bên trong góc nội tiếp thì được gọi là cung bị chắn.
Ví dụ: Ở trong hình dưới đây, chúng ta có góc ACB là góc nội tiếp chắn cung AB.
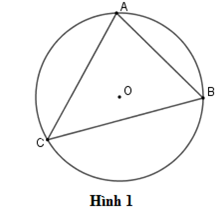
Định lý
Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn bởi góc đó.
Ví dụ: Ở trong hình 1, số đo của góc ACB bằng nửa số đo của cung AB.
Hệ quả
Trong một đường tròn:
a) Các góc nội tiếp số đo bằng nhau thì chắn các cung bằng nhau.
b) Các góc nội tiếp mà cùng chắn một cung hoặc chắn các cung bằng nhau thì có số đo bằng nhau.
c) Góc nội tiếp (có số đo nhỏ hơn hoặc bằng 90º) và góc ở tâm mà cùng chắn một cung, thì góc nội tiếp sẽ có số đo bằng một nửa số đo góc ở tâm.
d) Một góc nội tiếp chắn nửa đường tròn là một góc vuông.
4. Góc tạo bởi dây cung và tia tiếp tuyến
Định nghĩa:
Cho đường tròn có tâm O, cho tia Ax là tia tiếp tuyến tại tiếp điểm A và dây cung AB. Khi ấy, góc xAB là góc tạo bởi dây cung và tia tiếp tuyến.
Ví dụ : Góc xAB (hình 3) là góc được tạo bởi tia tiếp tuyến Ax với dây cung AB.
Định lý:
Số đo của một góc tạo bởi tia tiếp tuyến và dây cung bằng một nửa số đo của cung bị chắn.
Ví dụ: Số đo góc xAB (hình 1) bằng nửa số đo của cung nhỏ AB .
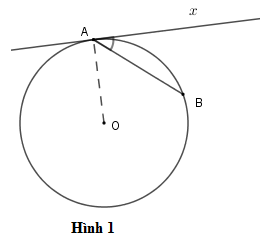
Hệ quả:
Trong cùng một đường tròn, góc được tạo bởi tia tiếp tuyến cùng với dây cung và góc nội tiếp cùng chắn một cung thì có số đo bằng nhau.
5. Góc có đỉnh nằm bên trong đường tròn, góc có đỉnh nằm bên ngoài đường tròn
a) Góc có đỉnh nằm bên trong đường tròn
Định nghĩa: Trong hình bên dưới, góc CIB và góc AID nằm trong đường tròn tâm O. Hai góc đó được gọi là góc có đỉnh nằm ở bên trong đường tròn.
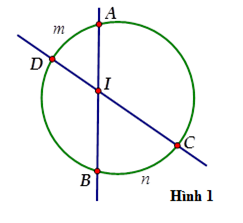
Định lý: Số đo của góc đỉnh nằm ở bên trong đường tròn bằng một nửa tổng số đo của hai cung bị chắn.
Ví dụ: Trong hình bên trên, góc CIB = 1/2(số đo cung AD + số đo cung BC)
b) Góc có đỉnh nằm bên ngoài đường tròn
Định nghĩa: Góc có đỉnh nằm ở bên ngoài đường tròn và các cạnh đều có điểm chung với đường tròn ( như trong hình 2,3,4) là góc có đỉnh nằm bên ngoài đường tròn.
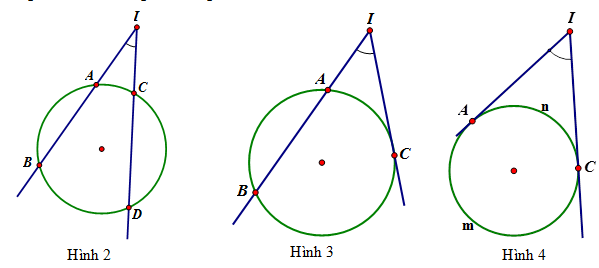
Định lý: Số đo của góc có đỉnh nằm ở bên ngoài đường tròn bằng một nửa hiệu số đo của hai cung bị chắn.
6. Đường tròn nội tiếp và đường tròn ngoại tiếp
Định nghĩa
Đường tròn mà đi qua tất cả các đỉnh của một đa giác thì được gọi là đường tròn ngoại tiếp đa giác và đa giác đó được gọi là đa giác nội tiếp đường tròn.
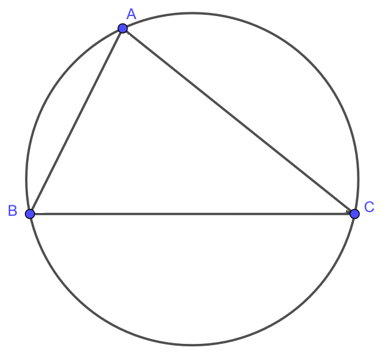
Ví dụ: Như hình trên, ta có đường tròn ngoại tiếp tam giác ABC.
Đường tròn mà tiếp xúc với tất cả các cạnh của một đa giác thì được gọi là đường tròn nội tiếp đa giác và đa giác đó được gọi là đa giác ngoại tiếp đường tròn.
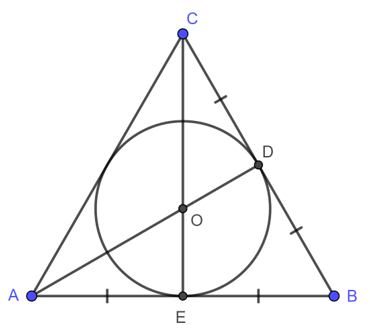
Ví dụ: Như hình trên, ta có đường tròn tâm O nội tiếp tam giác ACB.
Định lý
Bất kì đa giác đều nào thì cũng có duy nhất một đường tròn ngoại tiếp, duy nhất một đường tròn nội tiếp.
7. Tứ giác nội tiếp
Định nghĩa
Tứ giác nội tiếp của một đường tròn là tứ giác có bốn đỉnh nằm ở trên đường tròn đó.
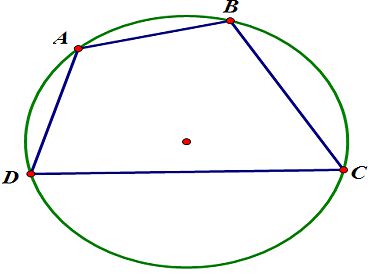
Định lý
– Trong một tứ giác nội tiếp, tổng số đo của hai góc đối diện nhau bằng 180 độ.
Ví dụ: Như trong hình trên, góc ABC + góc ADC = 180 độ; góc DAB + góc BCD = 180 độ.
– Ngược lại, một tứ giác có tổng số đo của hai góc đối diện bằng 180 độ thì tứ giác đó là tứ giác nội tiếp đường tròn.
Một số dấu hiệu nhận biết tứ giác nội tiếp
– Tứ giác có tổng của hai góc đối nhau bằng 180 độ.
– Tứ giác có số đo của góc ngoài tại một đỉnh bằng số đo của góc trong tại đỉnh đối với đỉnh đó.
– Tứ giác có bốn đỉnh cách đều một điểm O (có thể xác định được, O bất kỳ). Điểm O chính là tâm của đường tròn ngoại tiếp tứ giác đó.
– Tứ giác có hai đỉnh kề nhau và cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc là α.
Chú ý : Trong các dạng hình đã học thì hình thang cân, hình chữ nhật và hình vuông là những tứ giác nội tiếp đường tròn.
8. Độ dài của cung tròn, đường tròn
Công thức tính độ dài của đường tròn (chu vi đường tròn)
Cho đường tròn tâm O bán kính R (O;R), độ dài (C) của đường tròn (hay còn gọi là chu vi của đường tròn) chính là: C = 2πR hay C = πd với d = 2R là đường kính của đường tròn tâm (O).
Công thức tính độ dài cung tròn
Trên một đường tròn bán kính R, độ dài l của một cung nº sẽ được tính theo công thức là: l = πRn/180
9. Diện tích của hình quạt tròn, hình tròn
Công thức tính diện tích của hình tròn
Diện tích S của một hình tròn có bán kính R sẽ được tính theo công thức như sau:
S = πR²
Công thức tính diện tích của hình quạt tròn
Diện tích S của hình quạt tròn bán kính R, có cung nº sẽ được tính theo công thức:
S = πR²n/360 hay S = l.R/2 (Với l chính là độ dài cung nº của hình quạt tròn)
B. LUYỆN TẬP ÔN THI GIỮA HỌC KÌ 2 MÔN TOÁN LỚP 9
I. Các dạng toán thi giữa học kì 2 lớp 9
Dạng 1: Phương trình & hệ phương trình.
Dạng 2: Hàm số và đồ thị.

Dạng 3: Giải bài toán bằng cách lập phương trình, lập hệ phương trình.

Dạng 4: Hình học tổng hợp.

Dạng 5: Toán nâng cao.

II. Bài tập ôn thi giữa học kì 2 toán 9
1. Đề bài


2. Bài giải
Câu 1:
Phương pháp giải:
a) Ta sẽ sử dụng công thức nghiệm của phương trình bậc hai để giải đáp án.
b) Đặt x^2 = t (giá trị t lớn hơn hoặc bằng 0) để đưa phương trình ở đề bài thành phương trình bậc hai sau đó dùng công thức nghiệm để tìm t sau đó tìm x.

Câu 2:
Phương pháp giải:
a) Lập bảng giá trị sau đó vẽ đồ thị.
b) Lập phương trình hoành độ giao điểm, sau đó giải phương trình bậc hai để giải.
Bài giải:
a)
| x | -2 | -1 | 0 | 1 | 2 |
| y | -2 | -1/2 | 0 | -1/2 | -2 |
Vậy đồ thị hàm số đã cho là đường cong đi qua các điểm (-2;-2), (-1;-1/2), (0;0), (1;-1/2), (2;-2)
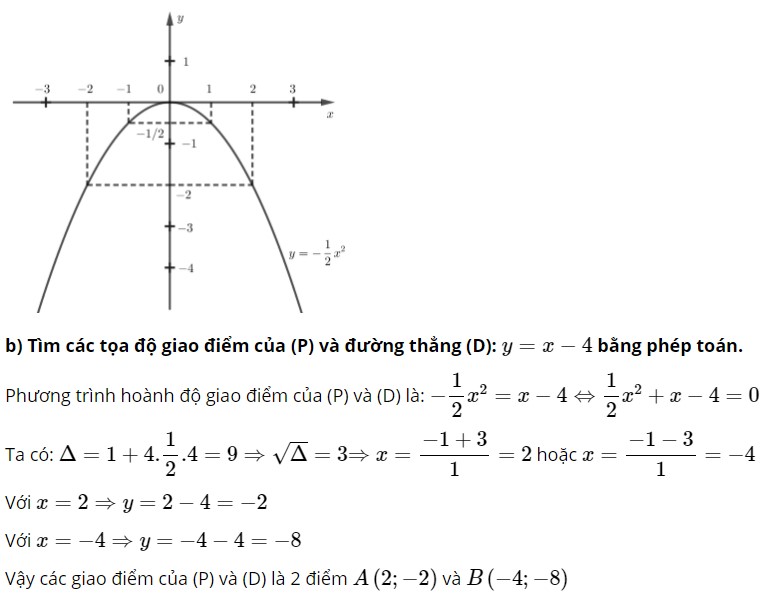
Câu 3:
Phương pháp giải:
Giải bài toán bằng cách lập một hệ phương trình để tìm ra chiều dài và chiều rộng khu vườn, sau đó hãy tính diện tích.
Diện tích của hình chữ nhật tính bằng tích của chiều dài và chiều rộng.

Câu 4:

Câu 5:
Phương pháp giải:
Chứng minh tam giác ABC vuông tại điểm A từ đó sẽ sử dụng mối quan hệ giữa góc và cạnh trong tam giác vuông để tính cạnh AB, cạnh AC.
Để tính ra diện tích của phần tô đậm ta lấy diện tích của nửa hình tròn tâm (O) đường kính BC trừ đi diện tích của tam giác ABC.

Câu 6:
Phương pháp giải:
a) Sử dụng công thức nghiệm thu gọn để thu về phương trình có hai nghiệm, thì delta có giá trị lớn hơn bằng 0.
b) Kết hợp với câu a), biến đổi biểu thức ở đề bài sao cho chỉ còn là: x1 + x2 và x1.x2 sử dụng hệ thức Vi-ét thế vào để tìm giá trị m.

Câu 7:
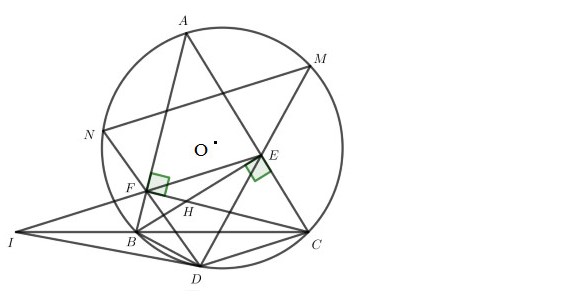
Phương pháp giải:
- Chứng minh bốn điểm A, E, H, F cùng nằm trên một đường tròn để suy ra rằng AEHF là tứ giác nội tiếp, chứng minh rằng tứ giác BCEF có hai đỉnh kề nhau cùng nhìn cạnh mà chứa hai đỉnh còn lại dưới cùng một góc là α.
- Chứng minh tam giác IBD và tam giác IDC là hai tam giác đồng dạng với nhau để suy ra điều phải chứng minh.
- Chứng minh hai góc ở vị trí đồng vị có giá trị bằng nhau dựa theo các định lý talet thuận và đảo để suy ra được các tam giác đồng dạng.
C. ĐỀ THI THAM KHẢO GIỮA HỌC KÌ 2 TOÁN LỚP 9
Trên đây là bài viết Ôn thi giữa học kì 2 toán lớp 9 mà HOCMAI muốn gửi tới các em học sinh. Kỳ thi này sẽ không còn khó nữa khi các em thật sự quyết tâm và chăm chỉ. HOCMAI chúc các em vượt qua kỳ thi thật tốt, đạt được điểm số mà mình đã đề ra. Các em có thể tìm thêm thật nhiều bài học hay khác tại hoctot.hocmai.vn nhé!





















