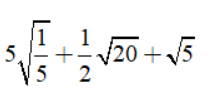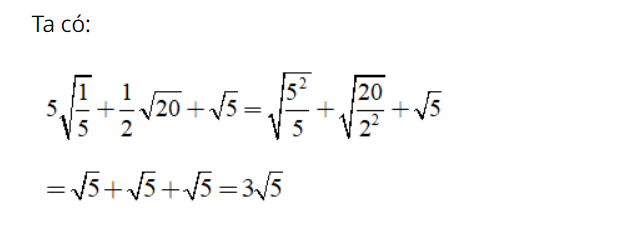A. Lý thuyết rút gọn biểu thức chưa căn bậc 2
1. Phương pháp rút gọn:
– Để có thể rút gọn biểu thức chứa căn bậc hai, các em học sinh cần vận dụng kết hợp các phép tính cũng như những phương pháp khai phương đã được học trong chương trình toán lớp 9.
– Khi đề bài yêu cầu rút gọn một dãy các phép tính cộng, trừ, nhân, chia, lũy thừa và khai phương, các em học sinh thực hiện các bước theo thứ tự sau: tiến hành khai căn trước rồi đến lũy thừa, sau đó đến nhân, chia, cộng, trừ.
2. Một số biểu thức chưa căn cần nhớ
#1. Sử dụng hằng đẳng thức √A²=|A|
#2. Áp dụng các công thức khai phương của một tích hoặc khai phương của một thương
#3. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
3. Một số ví dụ thực hành:
Ví dụ 1: Chứng minh đẳng thức sau
Hướng dẫn giải:
Ví dụ 2: Rút gọn biểu thức
Hướng dẫn giải:
Ví dụ 3: Rút gọn biểu thức sau:
Hướng dẫn giải:
B. Một số bài tập về rút gọn biểu thức chứa căn bậc 2
Hướng dẫn giải:
Hướng dẫn giải:
Tham khảo thêm:
Biến đổi đơn giản biểu thức chứa căn bậc 2
