“Hệ thức lượng trong tam giác vuông” là nội dung kiến thức cực kỳ quan trọng mà học sinh lớp 9 cần lưu ý ghi nhớ kỹ để học tốt và đạt điểm cao trong các bài kiểm tra môn Toán ở năm học cuối cấp. Dưới đây là những nội dung cần nắm vững kèm theo một số bài luyện tập thực hành trong bài giảng của thầy Nguyễn Hoàng Việt – Giáo viên Toán tại Hệ thống Giáo dục HOCMAI tại buổi học livestream của Lớp học online Toán – Văn miễn phí cùng HOCMAI (lớp 6 – 9). Phụ huynh và các con cùng tham khảo, theo dõi nhé.
I/ Hệ thống kiến thức
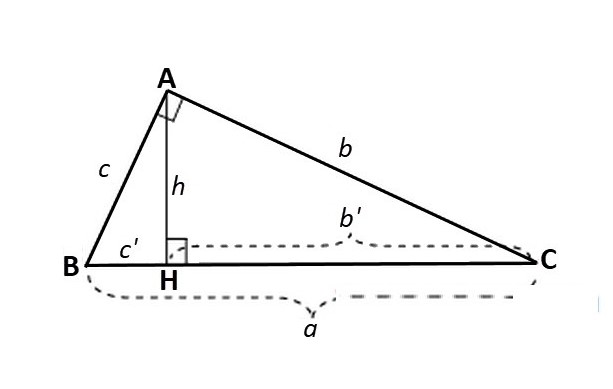
Mở đầu bài học, thầy Việt hệ thống lại một số kiến thức căn bản về hệ thức lượng trong tam giác vuông cho các bạn học sinh ghi nhớ. Theo đó, giả sử cho tam giác ABC vuông tại A, đường cao AH. Khi đó:
AB, AC là các cạnh góc vuông;
BC là cạnh huyền;
BH, CH lần lượt là các hình chiếu của AB, AC lên BC.
Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP
Lúc này, ta có các hệ thức:
– Định lý Py-ta-go (lớp 7): a² = b² + c²
– Hệ thức về cạnh và hình chiếu: c² = c’.a ; b² = b’.a
– Hệ thức về đường cao và hình chiếu: h² = b’.c’
– Hệ thức về cạnh và đường cao: b.c = a.h ; 1/h² = 1/b² + 1/c²
II/ Bài tập vận dụng
Trong buổi học livestream “Một số hệ thức về cạnh và đường cao trong tam giác vuông”, thầy Việt đã chọn lọc và đưa ra một số bài tập có liên quan tới tính toán cạnh, chu vi và diện tích của một tam giác vuông. Với dạng bài này, thầy hướng dẫn thực hành phương pháp giải toán qua 3 bước sau, các em lưu ý ghi nhớ để áp dụng thành thục nhé:
| Bước 1:
Quan sát |
Xác định để tính diện tích tam giác cần biết độ dài cạnh nào, cạnh cần tính thuộc tam giác vuông nào. |
| Bước 2:
Áp dụng |
Sử dụng các hệ thức về cạnh và đường cao trong tam giác vuông phù hợp. |
| Bước 3:
Tính |
Thay số để tính cạnh và chu vi, diện tích (nếu cần). |
Cùng vận dụng kiến thức lý thuyết và áp dụng phương pháp giải toán vào các bài luyện tập dưới đây nhé.
Bài 1: Muốn tính khoảng cách từ điểm A đến điểm B nằm bên kia bờ sông, ông Tuấn vạch từ A đường vuông góc với AB. Trên đường vuông góc này lấy một đoạn thẳng AC = 30m, rồi vạch CD vuông góc với phương BC cắt AB tại D (xem hình vẽ). Đo được AD = 20m, từ đó ông Tuấn tính được khoảng cách từ A đến B. Em hãy tính độ dài AB, BC và CD.
Hướng dẫn:


Bài 2:
Câu a: Cho tam giác ABC vuông tại A; đường cao AH vuông góc với BC; AB = 3; AC = 4. Tính BC; HB; HC; AH.
Hướng dẫn:
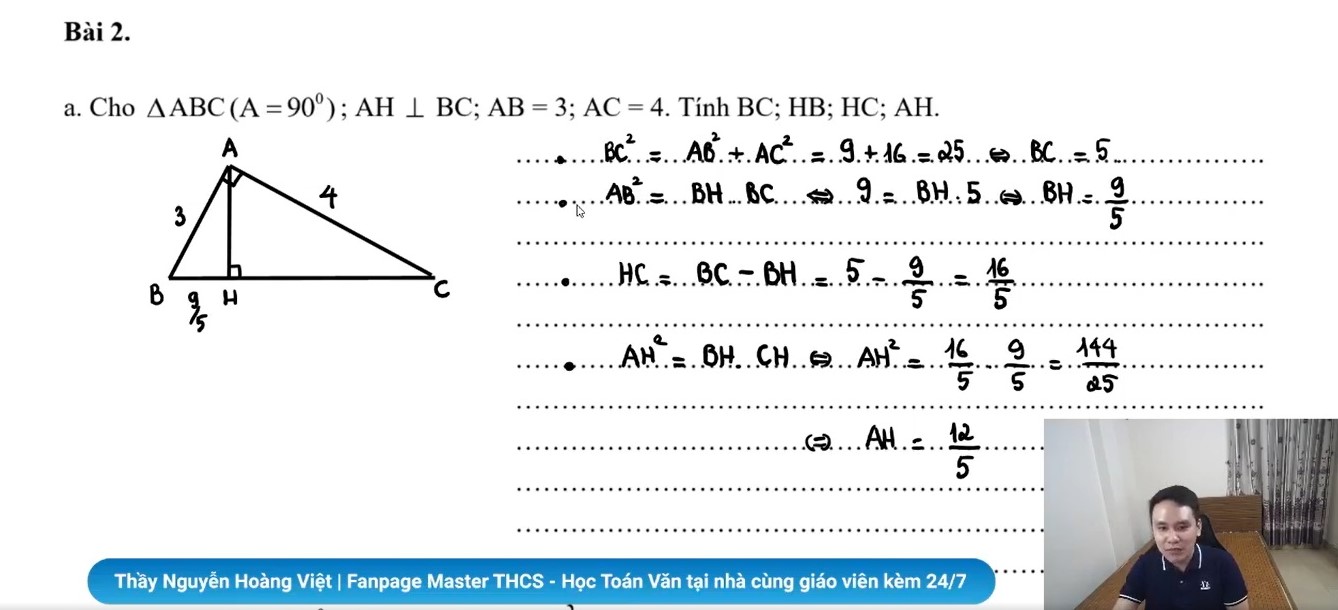
Áp dụng định lý Py-ta-go trong tam giác ABC vuông tại A, ta có:
BC² = AB² + AC² ⇔ BC² = 3² + 4² = 9 + 16 = 25 ⇔ BC = 5
Áp dụng hệ thức về cạnh góc vuông và hình chiếu trong tam giác vuông ABC, ta có:
AB² = BH.BC ⇔ 3² = BH.5 ⇔ 9 = BH.5 ⇔ BH = 9/5
Ta lại có:
CH = BC – BH = 5 – 9/5 = 16/5
Áp dụng hệ thức giữa đường cao và hình chiếu trong tam giác vuông ABC, ta có:
AH² = HB.HC ⇔ AH² = 9/5 x 16/5 = 144/25 ⇔ AH = 12/5
Vậy ta đã tính được độ dài các cạnh BC, AH, BH và CH.
Câu b: Cho tam giác ABC vuông tại A. Đường cao AH vuông góc với BC. Độ dài cạnh AB bằng 3/4 cạnh AC. BC = 30 cm. Tính AB, AC, HB, HC, HA và diện tích tam giác ABC.
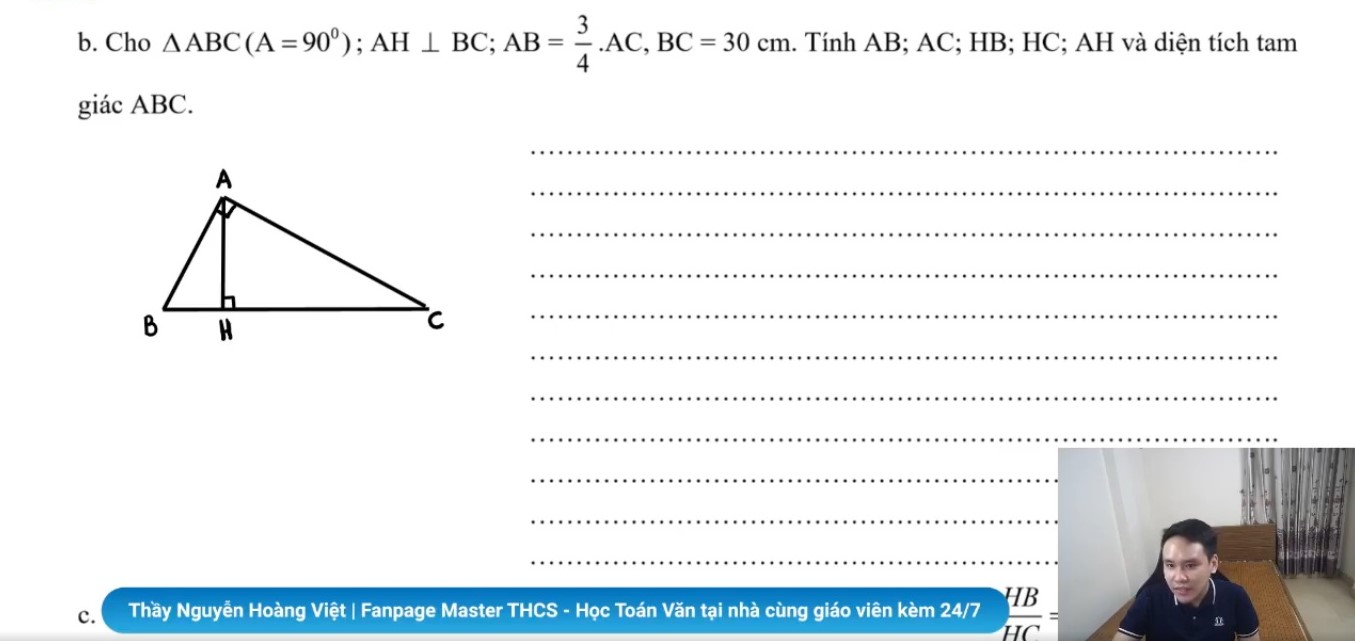
Hướng dẫn:
Áp dụng định lý Py-ta-go trong tam giác vuông ABC, ta có:
BC² = AB² + AC² ⇔ AB² + AC² = 30² = 900
⇔ (3/4 x AC)² + AC² = 900
⇔ 9/16 x AC² + AC² = 900
⇔ 25/16 x AC² = 900
⇔ AC² = 576
⇔ AC = 24 (cm)
Tính AB, ta có: AB = 3/4 x AC = 3/4 x 24 = 18 (cm)
Áp dụng hệ thức giữa cạnh và hình chiếu trong tam giác vuông ABC, ta có:
AB² = BH.BC ⇔ BH = AB² : BC ⇔ BH = 18² : 30 = 54/5 = 10,8 (cm)
Tính HC, ta có: HC = BC – BH = 30 – 54/5 = 96/5 = 19,2 (cm)
Tính AH, ta có: AH² = BH.HC ⇔ AH² = 10,8 x 19,2 = 207,36 ⇔ AH = 14,4 (cm)
Diện tích tam giác ABC là: AB.AC / 2 = 18.24 / 2 = 216 (cm²)
Câu c: Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Tính chu vi tam giác ABC biết AH = 14cm; HB/HC = 1/4
Hướng dẫn:


Câu d: Cho tam giác ABC vuông tại A. Độ dài cạnh AB = 12cm; AC = 16cm. Kẻ đường phân giác AD, đường cao AH. Tính HB, HC, HD và AD.
Hướng dẫn:
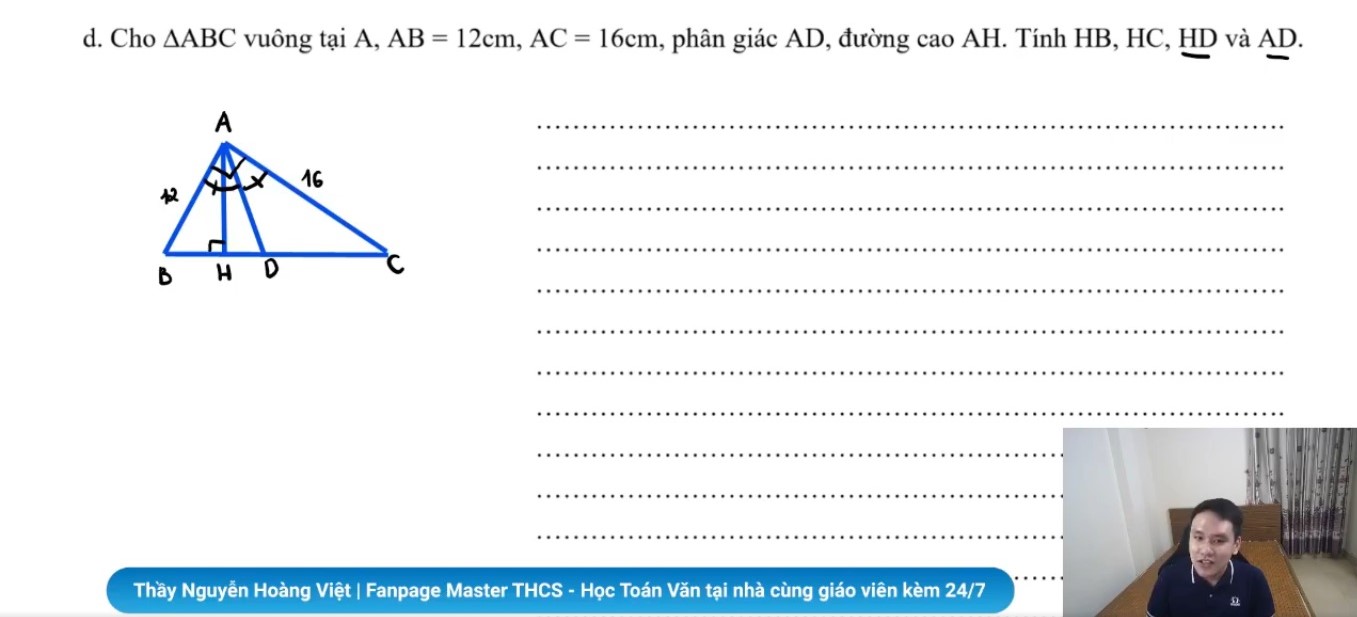
Áp dụng định lý Py-ta-go trong tam giác vuông ABC, ta có:
BC² = AB² + AC² = 12² + 16² = 400 ⇔ BC = 20 (cm)
Áp dụng hệ thức giữa cạnh và hình chiếu trong tam giác vuông, ta có:
AB² = BH.BC ⇔ 144 = BH.20 ⇔ BH = 36/5 (cm)
HC = BC – BH = 20 – 36/5 = 64/5 (cm)
Do AD là đường phân giác của tam giác ABC nên ta có:
BD/AB = DC/AC
= (BD + DC) / (AB + AC)
= BC / (AB + AC)
= 20 / (12 + 16) = 20/28 = 5/7
=> BD/AB = 5/7
=> BD = 12 x 5/7 = 60/7
=> HD = BD – BH = 60/7 – 36/5 = 48/35 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AHB, ta có:
AB² = AH² + HB² ⇔ 12² = AH² + (36/5)²
⇔ AH² = 144 – 1296/25 = 2304/25
⇔ AH = 48/5 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AHD, ta có:
AD² = AH² + HD² = (48/5)² + (48/35)² = 4608/49 => AD =![]()
Vậy ta đã tính được độ dài các cạnh HB, HC, HD và AD.
Trên đây là những kiến thức cần nắm vững và một số bài toán luyện tập trong bài giảng “Một số hệ thức về cạnh và đường cao trong tam giác vuông” của thầy Nguyễn Hoàng Việt. Năm học mới đã chính thức bắt đầu, học sinh các lớp khối THCS có thể tham gia Lớp học online Toán – Văn miễn phí cùng HOCMAI (lớp 6 – 9) để chủ động kiến thức, tự tin đạt điểm số cao.
Đây là lớp học livestream hoàn toàn MIỄN PHÍ cho tất cả học sinh các lớp 6 – 7 – 8 – 9 trên cả nước. Với mỗi buổi học, các em sẽ được trực tiếp tương tác với giáo viên, được hệ thống kiến thức trọng tâm và hướng dẫn giải các dạng bài tập. Đồng thời, các em cũng sẽ được định hướng, tư vấn lộ trình và kế hoạch học tập hợp lý, chuẩn bị cho chương trình môn Toán – Ngữ văn trong năm học mới 2021 – 2022.
>> ĐĂNG KÝ THAM GIA HỌC THỬ LỚP LIVE TOÁN 9 CÙNG THẦY HOÀNG VIỆT TẠI ĐÂY <<
 >> Để biết thêm thông tin chi tiết về khóa học, phụ huynh và học sinh hãy ĐĂNG KÝ NGAY TẠI ĐÂY để được TƯ VẤN MIỄN PHÍ!
>> Để biết thêm thông tin chi tiết về khóa học, phụ huynh và học sinh hãy ĐĂNG KÝ NGAY TẠI ĐÂY để được TƯ VẤN MIỄN PHÍ!

















![[HOCMAI] Chào năm mới 2024: ĐÓN TẾT RỒNG VÀNG – NHẬN QUÀ HOÀNH TRÁNG!](https://hoctot.hocmai.vn/wp-content/uploads/2024/01/1920x1080-100x70.png)

