A. Lý thuyết về hệ số góc của đường thẳng
1. Định nghĩa và khái niệm
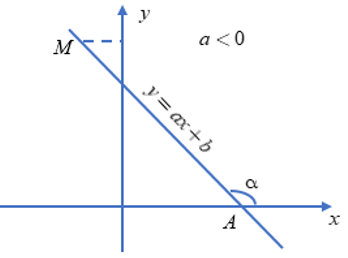
Ta có điểm A là giao điểm của đường thẳng y = ax + b với trục hoành Ox và có điểm M là một điểm thuộc đường thẳng và có tung độ dương. Lúc này ta có: ∠MAx là góc được tạo ả bởi đường thẳng y = ax + b với trục hoành Ox.
Biểu thị trên đồ thị như sau:
Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP

2. Hệ số góc của đường thẳng y = ax+b (a≠0)
Các đường thẳng có hệ số a bằng nhau (với a là hệ số của x) thì sẽ tạo với trục hoành Ox hệ số góc bằng nhau (Hệ quả từ tính chất của 2 đường thẳng song song)
Tham khảo thêm: Đường thẳng song song và đường thẳng cắt nhau
Trong trường hợp a > 0, góc được tạo bởi đường thẳng y = ax + b và trục hoành Ox là góc nhọn. Nếu hệ số a càng lớn thì góc đó càng lớn nhưng không vượt quá 90°.
Trong trường hợp a < 0, góc được tạo bởi đường thẳng y = ax + b và trục hoành Ox là góc Tù. Nếu hệ số a càng lớn thì góc đó càng lớn nhưng không vượt quá 180°.
Như vậy, góc được tạo ra bởi đường thẳng y = ax + b và trục hoành Ox luôn phụ thuộc vào hệ số a.
a cũng được gọi là là hệ số góc của đường thẳng y = ax + b (a≠0)
Lưu ý:
Đường thẳng y = ax + b (a≠0) cắt trục tung và trục hoành trong mặt phẳng Oxy 2 điểm là A (-b/a; 0) và B (0; b)
Vậy ta có một số kết luận sau:
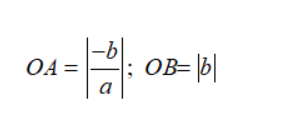
+ Khi a > 0, ta có:
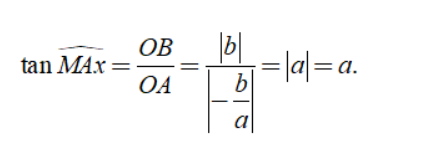
Lúc này, các em học sinh có thể sử dụng bảng lượng giác hay máy tính bỏ túi để tính ra được số đo của ∠MAx.
+ Khi a < 0 ta có:
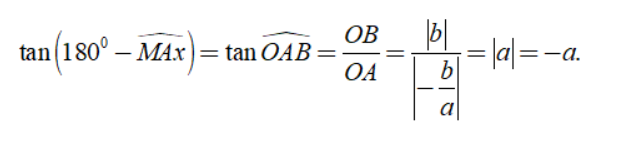
Từ biểu thức trên ta có thể tính được giá trị của (180° – ∠MAx), rồi tính được số đo ∠MAx.
+ Các đường thẳng có hệ số a bằng nhau (a là hệ số của x) thì song song với nhau và cùng tạo với trục Ox các góc bằng nhau.
+ Trong trường hợp b = 0, ta có hàm số y = ax. Đây là hàm số có đồ thị đi qua O là tâm đồ thị và a vẫn là hệ số góc của đường thẳng y = ax
B. Một số dạng bài về hệ số góc của đường thẳng y= ax+b
Dạng bài tập 1: Xác định hoặc tính hệ số góc của đường thẳng
Phương pháp giải:
Đường thẳng (d) có dạng y = ax+b (với a≠0) có a là hệ số góc của đường thẳng.
Ví dụ minh họa: Cho đường thẳng (d) có dạng y = 2x – 6. Vậy hệ số góc của đường thẳng (d) là a=2
Dạng bài tập 2: Tính góc được tạo bởi đường thẳng và trục hoành Ox
Phương pháp giải:
Ta có góc i được tạo bởi trục hoành Ox và đường thẳng (d) vậy ta có a = tani
Dạng bài tập 3: Viết phương trình đường thẳng hoặc tìm tham số m khi biết hệ số góc đã cho
Phương pháp giải:
Gọi phương trình đường thẳng cần tìm là (d): y = ax + b (a ≠ 0)
Dựa trên lý thuyết về hệ số góc, từ đó ta có thể tìm được giá trị của a. Sau đó, kết hợp với các dự kiện khác đã cho của đề bài để tìm ra b
C. Một số bài tập thực hành
Bài tập 1: Cho đường thẳng (d): y = x + 3. Hãy tính góc tạo bởi đường thẳng y = x + 3 với trục hoành Ox (làm tròn đến phút)
Hướng dẫn giải bài tập
Vẽ đồ thị hàm số y = x + 3
Ta có khi x = 0 thì y = 3 ta được điểm A (0; 2). Đây là giao điểm của (d) với trục tung Oy
Cho y = 0 thì x = -2 ta được điểm B (-2; 0).
Đồ thị hàm số đã cho đi qua hai điểm A(0; 2); B(-2; 0). Ta có đồ thị sau:
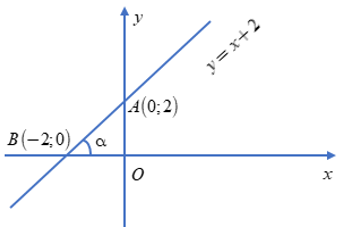
Gọi góc tạo bởi đường thẳng (d) y = x + 2 với trục Ox là α, ta có ∠ABO = α Xét tam giác vuông OAB. Từ đó ta suy ra:
tanα = OA/OB = 2/2 = 1 (1 chính là hệ số góc của đường thẳng d)
Vậy suy ra α = 45º
Bài tập 2: Cho đường thẳng d (d): y = ax + b . Tìm các giá trịnh a, b để đường thẳng (d) đi qua gốc tọa độ O và song song với (d’) biết đường thẳng (d’) có hệ số góc bằng 1
Hướng dẫn giải bài tập:
Theo điều kiện của đề bài đã ra ta có (d) đi qua gốc tọa độ nên đường thẳng (d) có dạng
y = ax
Do đường thẳng (d) song song với (d’) mà (d’) có hệ số góc bằng 1 nên hệ số góc a của đường thẳng d = 1
Vậy đường thẳng (d) có dạng: y = x
Trên đây là toàn bộ kiến thức và các dạng bài tập thường gặp về hệ số góc của đường thẳng y = ax + b trong chương trình Toán lớp 9. Hy vọng bài viết trên sẽ là cuốn sổ tay kiến thức hữu ích giúp các em học sinh dễ dàng giải quyết các dạng bài tập liên quan tới hệ số góc trong quá trình học và ôn thi.
Tham khảo thêm:
Nhắc lại và bổ sung các khái niệm về hàm số





















