Góc nội tiếp là kiến thức vô cùng quan trọng trong chương trình hình học Toán lớp 9. Đặc biệt các dạng bài tập Góc nội tiếp thường hay xuất hiện trong các bài kiểm tra, kỳ thi cuối kỳ hay chuyển cấp. Chính vì vậy, để giúp các em học sinh nhận biết, hiểu rõ và biết cách giải các dạng bài tập này. Hãy cùng HOCMAI tìm hiểu qua bài viết sau đây.
I. Tóm tắt Lý thuyết về Góc nội tiếp
1. Góc nội tiếp
Định nghĩa: Góc nội tiếp là góc có đỉnh nằm trên đường tròn và 2 cạnh chưa 2 dây cung của đường tròn đó.
Cung nằm bên trong góc được gọi là cung bị chắn.
Ví dụ: Xét đường tròn tâm O như hình vẽ:
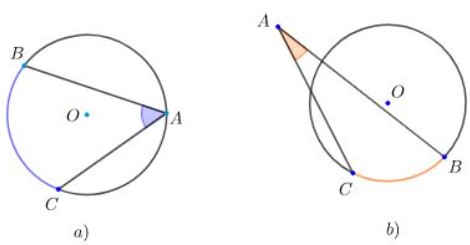
a) Góc BAC ở hình a là góc nội tiếp đường tròn tâm O vì có đỉnh A nằm trên đường tròn, hai dây AB,AC là dây của (O).
Cung BC (phần cung có màu xanh) được gọi là cung bị chắn.
b) Góc BAC ở hình b không phải là góc nội tiếp đường tròn (O) vì có đỉnh A là điểm nằm ngoài đường tròn (O).
Cung BC (phần cung tròn màu cam) không được gọi là cung bị chắn.
Như vậy, để chỉ ra một góc không phải là góc nội tiếp, ta chỉ cần chỉ ra góc đó không thỏa mãn một trong những điều kiện sau:
- Đỉnh của góc không nằm trên đường tròn.
- Có ít nhất một cạnh không chứa dây cung của đường tròn.
2. Định lý
Định lý: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo cung bị nó chắn.
Chứng minh định lý:
Xét đường tròn tâm O và góc BAC nội tiếp đường tròn tâm O. Ta cần chứng minh:
Góc BAC = 1/2 số đo cung BC
Để chứng minh định lý trên, ta xét 3 trường hợp:
a) Tâm O nằm trên một cạnh góc BAC.
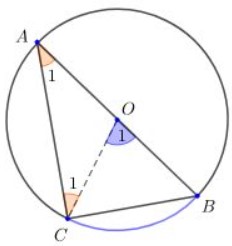
Từ hình vẽ, ta có: A,C ∈ (O) nên OA = OC)
=> ΔOAC cân tại O
=> Góc A1 = Góc C1 (2 góc ở đáy)
Dựa vào định lý về góc ngoài tam giác, ta sẽ có:
Góc O1 = Góc A1 + Góc C1 (Mà Góc A1 =Góc C1)
=> Góc O1 = 2 Góc A1
=> Góc A1 = 1/2 Góc O1 (1)
Lại có Góc O1 là góc ở tâm chắn cung nhỏ BC nên Góc O1 = Số đo cung BC. (2)
Từ (1) và (2) => Góc A1 = 1/2 số đo cung BC. Hay góc BAC = 1/2 số đo cung BC (ĐPCM).
b) Tâm O nằm trong góc BAC.
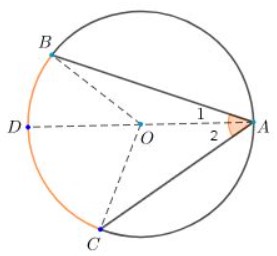
Kẻ đường kính AD. Khi đó góc BAC được chia thành hai góc A1 và góc A2 có một cạnh AD chứa tâm O của đường tròn. Theo kết quả từ câu a, ta có:
- Góc A1 = 1/2 số đo cung BD
- Góc A2 = 1/2 số đo cung DC
Vì điểm O nằm trong góc BAC nên tia AO nằm gữa tia AB và AC, suy ra:
Góc BAC = góc A1 + góc A2 = 1/2 số đo cung BD + 1/2 số đo cung DC (3)
Lại có D là điểm thuộc cung tròn BC nên ta có:
số đo cung BD + số đo cung DC = số đo cung BC
=> 1/2 số đo cung BD + 1/2 số đo cung DC = 1/2 số đo cung BC. (ĐPCM).
c) Tâm O nằm bên ngoài góc BAC.
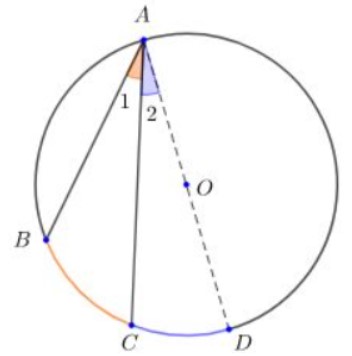
Kẻ đường kính AD. Khi đó hai góc A2 và góc BAD là hai góc có một cạnh AD chưa điểm O.
Theo kết quả câu a, ta có:
- Góc BAD = ½ số đo cung BD
- Góc A2 = số đo cung CD
Vì điểm O nằm ngoài góc BAC nên tia AC nằm giữa tia AB và AD. Nên ta có:
Góc BAD = góc A1 + góc A2
=> Góc A1 = góc BAD – góc A2 = 1/2 số đo cung BD – 1/2 số đo cung CD
=> Góc A1 = 1/2 ( số đo cung BD – số đo cung CD) = ½ số đo cung BC.
Vậy góc BAC = 1/2 số đo cung BC. (DPCM)
3. Tính chất của góc nội tiếp
Trong một đường tròn:
- Các góc nội tiếp bằng nhau thì chúng chắn các cung bằng nhau.
- Các góc nội tiếp chắn cùng một cung hoặc chắn các cung bằng nhau thì chúng bằng nhau.
- Góc nội tiếp (≤ 90°) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
- Góc nội tiếp chắn một nửa đường tròn là một góc vuông.
Ví dụ:
a) Các góc nội tiếp bằng nhau thì chắn các cung bằng nhau.
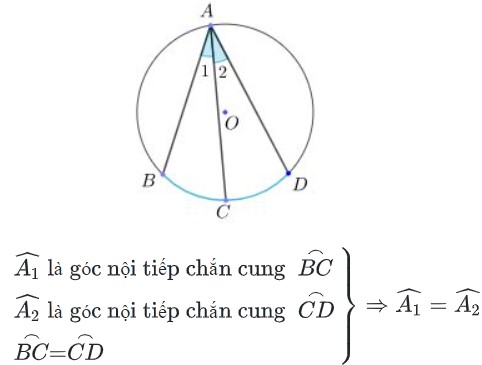
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
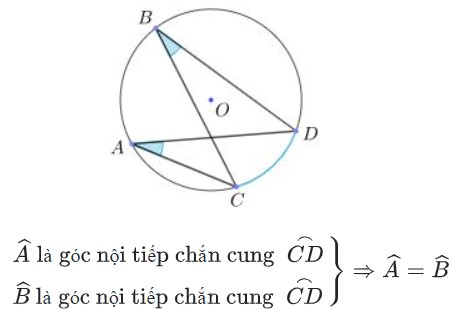
c) Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
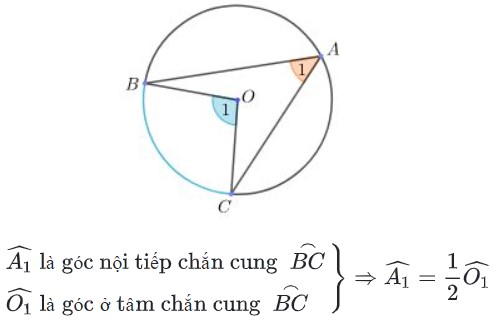
d) Góc nội tiếp chắn nửa đường tròn là góc vuông.
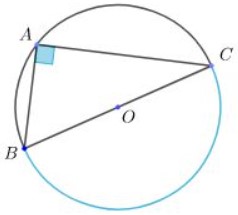
Góc A là góc nội tiếp cùng chắn BC chắn nửa đường tròn (O) => Góc A = 90°
II. Bài tập về Góc nội tiếp
Có tổng cộng 4 dạng bài tập về Góc nội tiếp. Bao gồm:
- Dạng 1: Chứng minh rằng hai góc bằng nhau; Tính số đo góc.
- Dạng 2: Tính độ dài và tính diện tích.
- Dạng 3: Bài toán dựa vào hệ quả của góc nội tiếp để chứng minh ba điểm thẳng hàng.
- Dạng 4: Bài toán dựa vào định lý, tính chất của góc nội tiếp để chứng minh hai đường thẳng vuông góc với nhau.
Để giải các dạng toán này, chúng ta cần áp dụng định nghĩa, định lý và các tính chất của góc nội tiếp để giải bài tập. Sau đây là một số câu hỏi trắc nghiệm và bài tập tự luận:
Bài tập trắc nghiệm
Câu 1: Cho tứ giác ABCD nội tiếp đường tròn tâm O như hình 1. Chọn khẳng định sai?
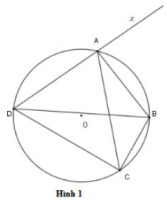
A. Góc BDC = Góc BAC
B. Góc ABC + Góc ADC = 180°
C. Góc DCB = Góc BAx
D. Góc BCA = Góc BAx
Lời giải:
Vì tứ giác ABCD là tứ giác nội tiếp nên góc BDC = góc BAC (hai góc nội tiếp cùng chắn cung BC)
- Góc ABC + góc ADC = 180° (Tổng hai góc đối bằng 180° )
- Góc DCB = góc BAx (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó).
Vậy D là đáp án chính xác
Câu 2: Nếu tứ giác ABCD là một tứ giác nội tiếp đường tròn. Chọn câu sai.
A. Góc BAD + góc BCD = 180°
B. Góc ABD = Góc ACD
C. Tổng 4 góc: Góc A + góc B + góc C + góc D = 360°
D. Góc ADB = Góc DAC
Trả lời:
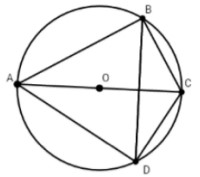
Ta có:
+) Góc BAD + Góc BCD = 180° (Tổng hai góc đối)
+) Góc ABD = Góc ACD (Hai góc nội tiếp cùng chắn cung AD)
+) Góc A + góc B + góc C + góc D = 360° (Tổng 4 góc trong tứ giác).
Vậy D là đáp án chính xác
Câu 3: Cho tam giác vuông ABC (vuông tại A) và đường cao AH. Kẻ HE vuông góc với AB tại E. kẻ HF vuông góc với AC tại F. Chọn câu đúng.
A. Tứ giác BEFC là một tứ giác nội tiếp.
B. Tứ giác BEFC không nội tiếp.
C. Tứ giác AFHE là một hình vuông.
D. Tứ giác AFHE không nội tiếp.
Trả lời:
Xét tứ giác AEHF, ta có:
Góc A = góc E = góc F = 90° => Tứ giác AEHF là một hình chữ nhật
AEHF là tứ giác nội tiếp (Vì tổng hai góc đối diện bằng 180°)
=> Góc AFE = Góc AHE (Hai góc cùng nhìn đoạn AE).
Góc AHE = Góc ABH (Cùng phụ góc BHE)
=> Góc AFE = Góc ABC ( = Góc AHE).
Xét tứ giác BEFC có: Góc AFE là góc ngoài tại đỉnh F và Góc AFE = Góc ABC
=> BEFC nội tiếp
=> Vậy A là đáp án chính xác
Bài tập tự luận
Câu 1: Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O). Gọi H là trực tâm tam giác ABC, điểm K là giao điểm thứ hai của AH với đường tròn tâm O. Đường thẳng đi qua điểm H và vuông góc với bán kính OA cắt BC tại điểm I. Chứng minh rằng tiếp tuyến của đường tròn tâm O là IK.
Lời giải:
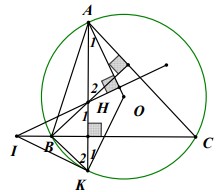
Dễ dàng chứng minh H đối xứng với K qua BC => Góc K2 = Góc H1 = Góc H2 (1)
Ta lại có góc K1 = góc A1 nên Góc K1 phụ Góc H2 (2)
Từ (1) và (2) => Góc K2 phụ góc K1 => IK là tiếp tuyến của (O).
Bài 2: Cho ΔABC nhọn có góc BAC = 45° nội tiếp đường tròn (O). Các đường cao BH,CK cắt đường tròn (O) lần lượt tại E và D. Chứng minh rằng 3 điểm D,O, E nằm trên 1 đường thẳng.
Lời giải:
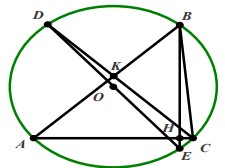
Ta có: Ta có: BH ⊥ AC => ΔABH vuông tại H
Mà góc BAH = 45° => góc ABH = 45° hay góc EBA = 45° (1)
Mặt khác có CK ⊥ AB => ΔACK vuông tại K
Mà góc KAC = 45° => góc KCA = 45°
Ta lại có góc DBA = góc DCA (Cùng chắn cung AD)
Nên góc ABD = 45° (2)
Từ (1)và (2) => góc EBD = góc DBA = góc ABE = 90°
=> DE là đường kính của (O) hay D,O, E thẳng hàng.
Bài 3: Cho tam giác ABC nội tiếp đường tròn (O) có bán kính 1dm, góc B = 45°, góc C =15°. Tính độ dài AC, BC, AB và diện tích tam giác ABC.
Lời giải:
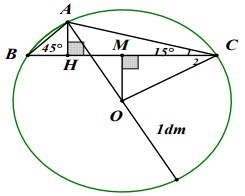
- Góc B = 45° => Góc AOC = 90° =? AC = OC√2 = √2 dm
- Kẻ OM ⊥ BC
Ta có góc C2 = góc C – góc C1 = 45° – 15° = 30°
=> MC = OC.cos 30° = √3/2 => BC = √3 dm
- Kẻ AH ⊥ BC, đặt HC = x, HB = y thì x + y = √3 (1)
Ta có HC² + HB² = HC² + HA² = AC² = 2 => x² + y² = 2 (2)
Từ (1) và (2) => 2xy = (x + y)² – (x² + y²) = 3 – 2 = 1 (3)
Từ (2) và (3) => (x – y)² = x² + y² – 2xy = 2 – 1 = 1 => x – y =1 (4)
Từ (1) và (4) => y = (√3 – 1)/2 dm => AB = y√2 = (√6 – √2)/2 dm
- SΔABC = 1/2 BH.AC = 1/2.√3.(√3 – 1)/2 = (√3 – 3)/4 (dm²)
Bài 4: Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O), đường trung tuyến AM. Trên cung BC lấy điểm D (Không chứa A) sao cho: Góc BAD = góc CAM. Chứng minh rằng hai góc ADB và góc CDM bằng nhau.
Lời giải:
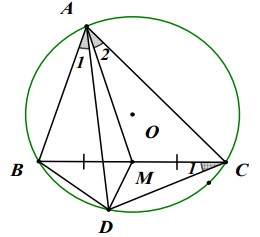
Góc A1 = Góc A2 => Góc BAM = Góc DAC,
Lại có Góc ABM = Góc ADC (Góc nội tiếp) nên ΔABM ∼ ΔADC (góc – góc)
=> BA/AD = BM/DC = MC/CD.
Kết hợp với góc A1 = góc C1 => ΔBAD ∼ ΔMCD (canh – góc – cạnh) => Góc ADB = Góc CDM (DPCM)
Xem lại nội dung bài viết và các dạng bài tập ( Trắc nghiệm + Tự luận có đáp án) tại đây:
Vừa rồi là bài viết hướng dẫn giải bài tập góc nội tiếp của HOCMAI. Hy vọng bài viết này sẽ giúp các em học sinh có thêm kiến thức, tài liệu bổ ích để học tập và ôn luyện. Nếu muốn tìm thêm những tài liệu, thông tin liên quan đến các môn học, đừng quên truy cập hoctot.hocmai.vn thường xuyên để theo dõi và cập nhật những bài viết mới nhất bạn nhé!
















