Liên hệ giữa cung và dây là kiến thức nền tảng để các em học sinh có thể giải các bài tập liên quan từ cấp độ cơ bản tới nâng cao trong chương trình hình học Toán 9, những bài thi chuyển cấp và cả trong đề thi Đại học. Để giúp các em nắm chắc kiến thức, HOCMAI đã tổng hợp những yếu tố tạo thành mối quan hệ giữa cung và dây và bài tập minh họa qua bài viết dưới đây.
Bài viết tham khảo thêm:
Định nghĩa về cung và dây
Tìm hiểu về Cung của đường tròn
Trong hình học không gian, Cung là một phần chu vi của một đường tròn khép kín. Ngoài ra Cung tròn còn được hiểu là tập hợp tất cả các điểm thuộc đường tròn nằm ở giữa hai đầu mút đã định sẵn. “⌒” Là ký hiệu biểu thị Cung tròn.
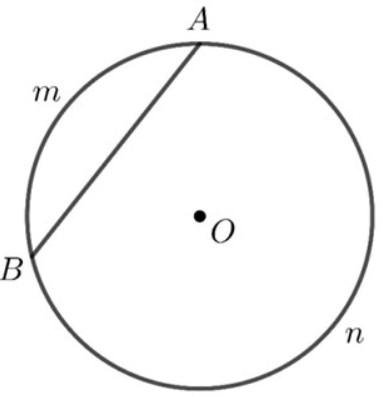
Cách tính cung của một đường tròn là đo góc tạo bởi hai đoạn thẳng rồi áp dụng công thức với L là chiều dài cung tròn:
Số đo góc của cung/360° = L/ Chu vi đường tròn
Tìm hiểu về dây cung của đường tròn
Dây hay dây cung của một đường tròn được hiểu là một đoạn thẳng nối từ hai điểm nằm trên một đường tròn.
Một dây cung được chứa bởi một đường thẳng thì được đường thẳng ấy được gọi là một cát tuyến.

Các tính chất đặc biệt của dây cung:
- Hai dây cung cùng nằm trong một đường tròn và cách đều tâm của đường tròn đó khi và chỉ khi chúng có độ dài bằng nhau.
- Đường trung trực của một dây cung đều đi qua tâm của đường tròn.
- Hai đường cát tuyến của hai dây cung cắt nhau tại một điểm thì có tính chất phương tích của một điểm.
- Trong một đường tròn, nếu hai dây cung chắn hai góc bằng nhau hoặc hai góc đó cùng được chắn bởi một dây cung thì hai góc ấy bằng nhau.
Lý thuyết tổng quát về mối liên hệ giữa cung và dây
Định lý 1
Với hai cung nhỏ thuộc một đường tròn hoặc trong hai đường tròn bằng nhau:
a) Hai cung bằng nhau => Căng hai dây bằng nhau.
b) Hai dây bằng nhau => Căng hai cung bằng nhau.
Định lí 2
Với hai cung nhỏ trong cùng một đường tròn hay trong hai đường tròn bằng nhau:
a) Cung lớn hơn thì căng dây lớn hơn.
b) Dây lớn hơn thì căng cung lớn hơn.
Các đặc điểm nên lưu ý về mối liên hệ giữa cung và dây
Trong cùng một đường tròn:
- Nếu hai cung được tạo thành bởi hai dây cung chắn song song với nhau thì chúng có độ lớn bằng nhau.
- Nếu đường kính đi qua điểm chính giữa của một cung tròn thì nó sẽ đi qua trung điểm của dây cung chắn cung tròn đó.
- Nếu đường kính đi qua trung điểm của dây cung và không đi qua tâm đường tròn thì nó sẽ đi qua điểm chính giữa của cung được tạo ra bởi dây cung đó.
- Nếu bán kính vuông góc với dây cung thì nó đi qua điểm nằm chính giữa của cung được tạo thành.
Bài tập tự luận và trắc nghiệm về so sánh dây cung và cung tròn
Phương pháp giải: Để giải các dạng bài tập về Liên hệ giữa cung và dây, chúng ta cần áp dụng các định lý, đặc điểm nên lưu ý đã nêu ở phần II.
- Hai cung tròn có độ lớn bằng nhau khi hai dây cung chắn hai cung tròn đó có độ dài bằng nhau.
- Hai dây cung có độ dài bằng nhau khi hai cung tròn bị chắn bởi 2 dây cung đó có độ lớn bằng nhau.
- Cung tròn nào nhỏ hơn thì sẽ có dây cung nhỏ hơn và ngược lại.
- Dây cung tròn nào có độ dài nhỏ hơn thì sẽ có cung tròn nhỏ hơn và ngược lại.
Bài tập tự luận:
Bài tập 1: Cho đường tròn tâm O có đường kính là AB và cung AC có số đo < 90°. Vẽ dây CD vuông góc với đường kính AB và dây DE // AB. Chứng minh: Cung AC = Cung BE.
Lời giải:
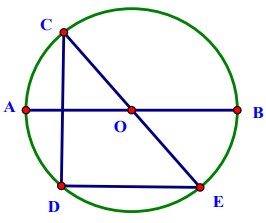
Ta có: CD vuông góc AB và AB // DE => CD vuông góc DE => CE là đường kính của (O).
Từ đó chứng minh được: ΔAOC = ΔBOE (cạnh – góc – cạnh)
=> Cung AC = Cung BE.
Bài tập 2: Cho hai hình vẽ a và b:
a) Vẽ đường tròn (O; R = 2cm). Hãy chỉ cách để vẽ cung AB có số đo bằng 60°. Hỏi dây AB có độ dài bao nhiêu cm.
b) Làm cách nào có thể chia đường tròn thành sáu cung bằng nhau như hình b.
Lời giải:
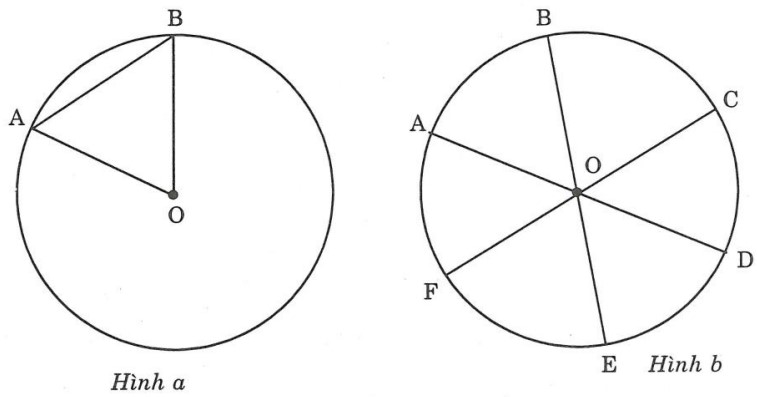
a) Cách để vẽ cung AB có số đo bằng 60°
Vẽ đường tròn (O; R = 2cm). Lấy điểm A bất kỳ trên đường tròn này là tâm, vẽ đường tròn tâm A bán kính AB = 2cm cho cắt (O) tại B. Nối A và B với O ta được:
ΔAOB (vì đường tròn tâm A có bán kính AB = 2cm nên đi qua O) có OA = AB = BO
=> ΔAOB đều => Góc AOB = 60° => Số đo cung AB = 60° (Theo định lý: Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó)
b) Cách để chia đường tròn thành 6 cung bằng nhau
Vẽ đường tròn tâm O bán kính ngẫu nhiên. Trên đường tròn này ta lấy một điểm A bất kỳ. Sau đó vẽ đường tròn tâm A có bán kính là OA cho cắt đường tròn tâm O tại tiếp điểm B.
Vẽ tiếp đường tròn tâm B có bán kính là OB và cho cắt đường tròn (O) tại tiếp điểm C. Vẽ các đường kính AD, BE, CF của đường tròn (O) ta được 6 cung AB = BC = CD = DE = EF = FA.
Bài tập 3:
Cho tam giác ABC. Trên tia đối của AB lấy một điểm D sao cho AD bằng AC. Vẽ đường tròn (O) ngoại tiếp ΔDBC. Từ tâm O hạ lần lượt các đường vuông góc: OH, OK với BC và BD ( Trong đó: H ∈ BC; K ∈ BD)
a) Chứng minh rằng cung OH > cung OK
b) So sánh hai cung nhỏ: cung BD cung và BC.
Lời giải:
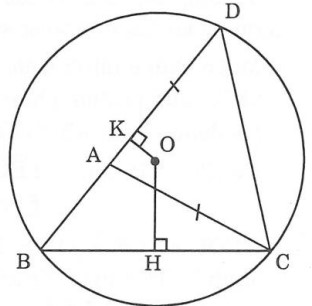
a) Chứng minh OH > OK
Muốn chứng minh OH > OK ta phải chứng minh BC < BD
Muốn chứng minh được bất đẳng thức BC < BD ta phải sử dụng bất đẳng thức tam giác với ΔABC ta có :
BC < AB + AC mà AC = AD (giả thiết)
=> BC < AB + AD
=> BC < BD
Với đường tròn (O) ngoại tiếp ΔBCD có dây BD lớn hơn dây BC. Theo định lý về dây cung và khoảng cách từ dây đến tâm: Trong hai dây của một đường tròn, dây nào lớn hơn thì gần tâm hơn.
Do đó cung OK < cung OH
b) So sánh hai cung nhỏ: cung BD cung và BC.
Dựa vào câu a => OK < OH => BD > BC (Theo định lý : Trong hai dây cùng một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn).
Bài tập 4:
a) Chứng minh rằng: Nếu đường kính đi qua điểm chính giữa của một cung thì nó đi qua trung điểm của dây căng cung ấy.
b) Mệnh đề đảo có đúng không? Hãy đưa thêm điều kiện để mệnh đề đảo đúng.
Lời giải
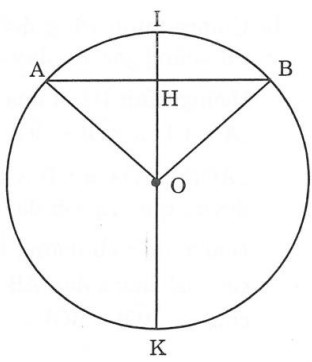
a) Muốn chứng minh HA = HB ta dựa vào giả thiết: “Cung IA = Cung IB”
Từ Cung IA = Cung IB => Số đo cung IA = Số đo cung IB (Theo định lý: Với hai cung nhỏ trong một đường tròn hay hai đường tròn bằng nhau: Hai cung bằng nhau căng hai dây bằng nhau)
=> I cách đều A và B. Lại có OA = OB (vì cũng là bán kính của đường tròn (O) mà I và O là hai điểm nằm ở hai phía của đoạn thẳng AB => I và O nằm trên đường trung trực của đoạn thẳng AB => H là trung điểm của dây AB.
b) Chứng minh mệnh đề đảo:

Muốn chứng minh cung IA = cung IB phải chứng minh được góc O1 = góc O2.
Muốn chứng minh được góc O1 = góc O2 ta chứng minh ΔAOB cân tại O
ΔAOB có OA = OB (cùng là bán kính một đường tròn) => ΔAOB cân tại O (Tam giác có hai cạnh bằng nhau là tam giác cân) => Trung tuyến OH thuộc đáy AB vừa là phân giác của góc AOB vừa là đường cao ứng đáy AC => góc O1 = góc O2
Số đo cung IA = Số đo cung IB (Theo định lí: Số đo của hai cung nhỏ bằng số đo của góc ở tâm chắn cung đó).
Điều kiện: Vậy cũng có OH vuông góc AB và HA = HB (Tính chất của tam giác cân). Ngược lại nếu đường kính OI vuông góc AB thì góc O1 = góc O2 => cung IA = cung IB.
Bài tập trắc nghiệm
Câu 1: Chọn khẳng định đúng.
Cho đường tròn tâm O có dây AB > dây CD, khi đó:
A. Cung AB lớn hơn cung CD
B. Cung AB nhỏ hơn cung CD
C. Cung AB bằng cung CD
D. Số đo cung AB = 2 lần số đo cung CD.
Lời giải:
Với hai cung nhỏ nằm trong cùng một đường tròn hoặc trong hai đường tròn bằng nhau:
- Nếu cung lớn hơn thì nó căng dây lớn hơn
- Nếu dây lớn hơn thì nó căng cung lớn hơn
Nên dây AB > dây CD => cung AB > cung CD
Vậy: A là đáp án đúng
Câu 2: Chọn khẳng định đúng.
Cho đường tròn tâm O có cung MN bé hơn cung PQ, khi đó:
A. MN > PQ
B. MN < PQ
C. MN = PQ
D. PQ = 2MN
Lời giải:
Với hai cung nhỏ nằm trong cùng một đường tròn hoặc trong hai đường tròn bằng nhau:
- Nếu cung lớn hơn thì nó căng dây lớn hơn
- Nếu dây lớn hơn thì nó căng cung lớn hơn
Nên cung MN < cung PQ => MN < PQ
Vậy: B là đáp án đúng
Câu 3: Chọn khẳng định đúng.
A. Trong cùng một đường tròn, đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm ở chính giữa của cung bị căng bởi dây ấy.
B. Trong một đường tròn, nếu đường kính đi qua trung điểm của một dây thì nó đi qua điểm ở chính giữa của cung bị căng bởi dây ấy.
C. Trong một đường tròn, nếu đường kính đi qua điểm ở chính giữa của một cung nó thì song song với dây căng cung ấy.
D. Trong cùng một đường tròn, hai đường kính luôn luôn vuông góc với nhau.
Lời giải:
Theo các đặc điểm nên lưu ý về mối liên hệ giữa cung và dây đã nêu ở phần II. Ta dễ dàng tìm được đáp án của câu hỏi này.
Vậy: A là đáp án đúng
Xem full 30 câu trắc nghiệm về liên hệ giữa cung và dây tại đây
Mong rằng qua bài viết trên, HOCMAI đã giúp các em học sinh nắm rõ được mối các kiến thức cần nhớ và cách áp dụng các định lý để giải bài tập Toán 9 về liên hệ giữa cung và dây. Đừng quên truy cập vào thường xuyên cập nhật những bài viết mới nhất và học thêm kiến thức của các môn học.


















