Trong chương trình học Toán lớp 9, liên hệ giữa dây và khoảng cách từ tâm đến dây là chuyên đề quan trọng. Giúp các em học sinh có kiến thức nền tảng để giải các bài toán hình học không gian. Để hiểu được lý thuyết và các dạng bài tập thường gặp, hãy cùng HOCMAI theo dõi bài viết sau nhé!
I. Lý thuyết về Liên hệ giữa dây và khoảng cách từ tâm đến dây
Định lý 1
Trong một đường tròn:
a) Hai dây bằng nhau thì cách đều tâm
b) Hai dây cách đều tâm thì bằng nhau
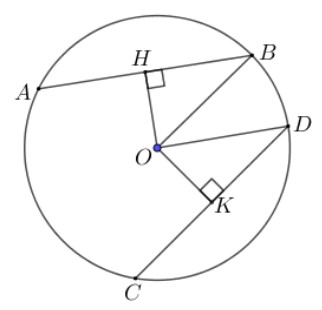
Chứng minh định lý:
Cho đường tròn (O) có hai dây AB và CD khác đường kính. Kẻ dây OH vuông góc dây AB; dây OK vuông góc dây CD. Hãy chứng minh:
a) Nếu AB = CD thì OH = OK
b) Nếu OH = OK thì AD = CD
Chứng minh:
a) Ta có:
- OH vuông góc AB => AB = 2HB (Vì đường kính vuông góc với dây cung)
- OK vuông góc CD => CD = 2KD (Vì đường kính vuông góc với dây cung)
Theo bài ra: AB = CD => HB = KD (1)
Áp dụng định lý Pytago vào hai tam giác vuông OHB và OKD, ta có:
- OH² + HB² = OB² = R² => OH² = R² – HB²
- OK² + KD² = OD² = R² => OK² = R² – KD²
Từ (1) => OH = OK
Vậy trong 1 đường tròn, hay dây có kích thước bằng nhau thì cách đều tâm.
b) Theo giả thuyết OH = OK => OH2 = OK2
Áp dụng định lý Pytago vào hai tam giác vuông OHB và OKD, ta có:
- OH² + HB² = OB² = R² => HB² = R² – OH²
- OK² + KD² = OD² = R² => KD² = R² – OK²
=> HB = KD. Từ (1) => AB = CD
Vậy trong cùng 1 đường tròn, hai dây cách đều tâm thì có kích thước bằng nhau.
Định lí 2
Trong hai dây của một đường tròn
a) Dây nào lớn hơn thì dây đó gần tâm hơn
b) Dây nào gần tâm hơn thì dây đó lớn hơn
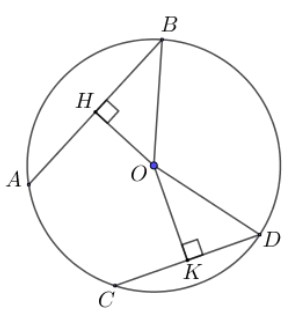
Chứng minh định lý:
Cho đường tròn (O) có hai dây AB và CD khác đường kính. Kẻ dây OH vuông góc dây AB; dây OK vuông góc dây CD. Khi đó:
a) Nếu AB < CD thì OH > OK.
b) Nếu OH < OK thì AB > CD
Chứng minh:
a) Theo bài ra ta có:
OH vuông góc AB => AB = 2HB (Vì đường kính vuông góc với dây cung)
- OK vuông góc CD => CD = 2KD (Vì đường kính vuông góc với dây cung)
Theo bài ra: AB = CD => HB = KD (1)
Từ giả thuyết: AB > CD => HB > KD => HB2 > KD2
Vậy trong hai dây của một đường tròn, dây nào có kích thước lớn hơn thì dây đó gần tâm hơn.
b) Áp dụng định lý Pytago vào hai tam giác vuông OHB và OKD, ta có:
- OH² + HB² = OB² = R² => HB² = R² – OH²
- OK² + KD² = OD² = R² => KD² = R² – OK²
Theo giả thuyết OH < OK => OH2 < OK2 => HB2 < KD2
Từ (1) suy ra AB2 > CD2 => AB > CD
Vậy trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó có kích thước lớn hơn.
II. Bài tập vận dụng Liên hệ giữa dây và khoảng cách từ tâm đến dây
Bài 1: (12/106/SGK TOÁN 9 T1)
Cho đường tròn (O) bán kính R = 5cm, dây AB = 8cm
a) Tính khoảng cách từ tâm O đến dây AB
b) Gọi I là điểm trên dây AB với AI = 1cm, kẻ dây CD qua I và vuông góc với AB. Chứng minh rằng CD = AB
Lời giải:
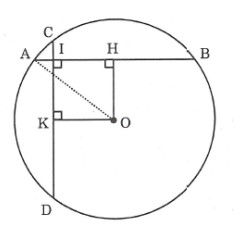
a) Kẻ OH vuông góc AB tại H

Bài 2: (13/106/SGK TOÁN 9 T1)
Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại E nằm bên ngoài đường tròn. Gọi điểm H và điểm K là trung điểm của AB và CD.
a) Chứng minh EH = EK
b) Chứng minh EA = EC
Lời giải:
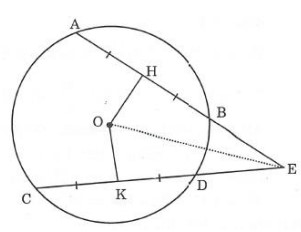
a) Chứng minh EH = EK
Ta sẽ làm theo cách: Muốn chứng minh hai đoạn thẳng bằng nhau, ta chứng minh hai tam giác chứa hai đoạn thẳng đó bằng nhau.
- Tam giác nào chứa đoạn thẳng EH và tam giác nào chứa đoạn thẳng EK?
- Tam giác OHE chứa đoạn EH? Tam giác OKE chứa đoạn EK? ΔOHE và ΔOKE có bằng nhau không?
Ta thấy ΔOHE và ΔOKE có một cạnh chung là OE. Ta phải tìm các yếu tố bằng nhau khác để đủ điều kiện kết luận ΔOHE = ΔOKE.

Bài 3: (14/106/SGK TOÁN 9 T1)
Cho đường tròn (O) bán kính bằng 25cm, dây AB = 40cm . Vẽ dây CD // AB và có khoảng cách đến AB bằng 22cm. Tính độ dài CD.
Lời giải:
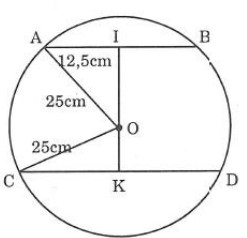
Kẻ OI vuông góc AB tại I; IO cắt CD tại K.

Bài 4: (15/106/SGK TOÁN 9 T1)
Cho hình như sau: Trong đó hai đường tròn có cùng tâm là O cho biết AB > CD. Hãy chứng minh:
a) OH < OK;
b) ME > MF;
c) MH > MK.
Lời giải:
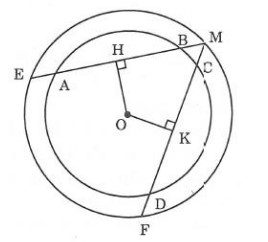
a) Chứng minh OH < OK
Làm thế nào để chứng minh OH < OK?
Muốn chứng minh được bất đẳng thức này là nghĩ ngay đến các định lí về đường tròn có sự so sánh khoảng cách từ dây đến tâm.

Bài viết tham khảo thêm:
- Tổng hợp kiến thức toán 9
- Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Đường kính và dây của đường tròn
Bài viết trên đã cung cấp cho các em kiến thức về lý thuyết và các dạng bài tập thường gặp về liên hệ giữa dây và khoảng cách từ tâm đến dây. Hy vọng những thông tin bổ ích này sẽ giúp cho các em học sinh trong quá trình học và ôn tập. Đừng quên thường xuyên truy cập hoctot.hocmai.vn để cập nhật thêm những kiến thức thú vị nhé!


















