Cùng HOCMAI tìm hiểu về chuyên đề Góc ở tâm. Số đo cung trong bài viết ngày hôm nay nhé! Bài viết sẽ bao gồm phần tóm tắt kiến thức cần nắm và phần hướng dẫn giúp các em học sinh giải các bài tập liên quan. Qua đó giúp các em củng cố lại kiến thức và hoàn thiện các kỹ năng làm bài.
Bài viết tham khảo thêm:
I. Tóm tắt kiến thức cần nắm về Góc ở tâm. Số đo cung
1. Góc ở tâm
Định nghĩa: Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm. Ví dụ: Góc AOB trong hình là góc ở tâm.
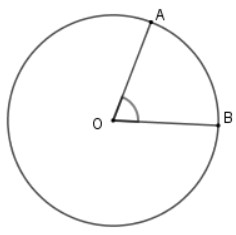
- Nếu 0° < góc AOB < 180° thì cung nằm bên trong góc được gọi là cung nhỏ, cung nằm bên ngoài góc được gọi là cung lớn.
- Nếu góc AOB = 180° thì mỗi cung là một nửa đường tròn.
- Cung nằm bên trong góc được gọi là cung bị chắn. Góc bẹt chắn nửa đường tròn.
2. Số đo cung
- Số đo của cung nhỏ bằng chính số đo của góc ở tâm chắn cung đó. Ví dụ: góc AOB = số đo cung AB (góc ở tâm chắn cung AB ) (Hình trên).
- Số đo của cung lớn bắn hiệu giữa 360° và số đo của cung nhỏ (Có chung hai đầu mút với cung lớn).
- Số đo của một nửa đường tròn bằng 180°. Cung của cả đường tròn có số đo 360°.
3. So sánh hai cung
Trong một đường tròn hoặc hai đường tròn bằng nhau:
- Hai cung được gọi là bằng nhau chi khi chúng có số đo bằng nhau.
- Trong hai cung, cung nào có số đo lớn hơn thì được gọi là cung lớn hơn.
4. Định lý
Nếu C làm một điểm nằm trên cung AB thì:
Số đo cung AB = số đo cung AC + số đo cung CB
II. Bài tập minh họa về Góc ở tâm – Số đo cung
Phương pháp giải: Để giải các dạng bài tập về Góc ở tâm – Số đo cung như: Tìm số đo của góc ở tâm; tính số đo của cung bị chắn, chúng ta cần sử dụng các kiến thức sau:
- Số đo của cung nhỏ bằng chính số đo của góc ở tâm chắn cung đó.
- Số đo của cung lớn bằng hiệu giữa 360° và số đo của cung nhỏ (có chung hai đầu mút với cung lớn).
- Số đo của một nửa đường tròn bằng 180°. Cung của cả đường tròn có số đo 360° .
- Sử dụng định lý tỉ số lượng giác của một góc nhọn để tính góc.
- Sử dụng quan hệ giữa đường kính và dây cung.
Bài tập tự luận:
Bài 1: Cho đường tròn (O; R). Vẽ dây AB = R2. Tính số đo của hai cung AB.
Lời giải:
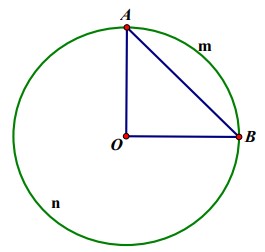
Ta có:
Tam giác AOB có: AB² = OA² +OB² vì (R2 )² = R² + R²
=> Tam giác AOB vuông tại O (Theo định lý Pytago đảo)
=> Góc AOB = 90° => Số đo cung AmB = 90° => Số đo cung AnB = 360° – 90° = 270°
Bài tập 2: Cho đường tròn (O; R). Vẽ dây AB sao cho số đo của cung nhỏ AB bằng một nửa số đo của cung lớn AB. Tìm diện tích của tam giác AOB.
Lời giải:
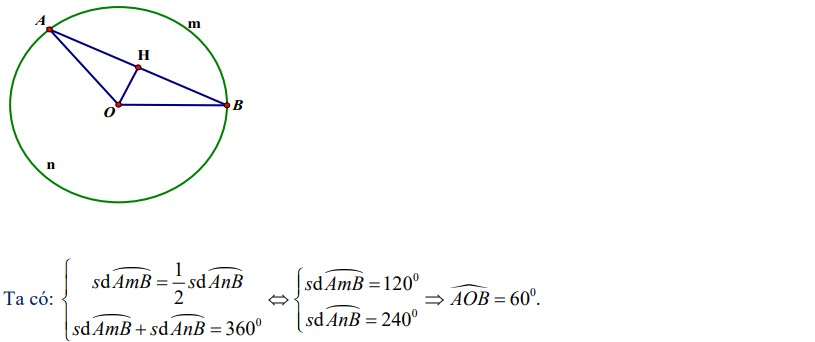
Kẻ OH vuông góc AB. Tam giác OAB cân tại O có OH là đường cao nên OH là phân giác của góc AOB và là đường trung tuyến của tam giác OAB. Do đó:
- AB = 2HA
- Góc AOH = 60°
Δ vuông AOH (tại H) Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông ta có:
- HA = OA.sin góc AOH = (R3)/2
- OH = OA.cos góc AOH = R/2
Diện tích của tam giác AOB là: S ΔAOB = 1/2.2AH.OH = AH.OH = (R²3)/4.
Bài tập 3: Cho đường tròn (O) và điểm M nằm ngoài đường tròn, vẽ hai tiếp tuyến MA và MB của đường tròn (O). Biết rằng góc AMB = 35°.
a) Tìm số đo góc ở tâm tạo bởi hai bán kính OA, OB.
b) Tìm số đo mỗi cung AB.
Lời giải:
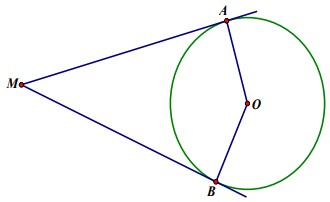
a) MA, MB là hai tiếp tuyến của (O) nên: góc OAM = 90°; góc OBM = 90° mà ta lại có:
Góc AMB = 35° => Góc AOB = 180° – 35° = 145°.
b) Vì góc AOB = 145° => Số đo cung AmB = 145° ; Số đo cung AnB = 360° – 145° = 215°.
Bài tập 4: Cho một tam giác đều ABC có ba đỉnh nằm trên một đường tròn tâm O.
a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB và OC.
b) Tính số đo các cung tạo bởi hai trong ba điểm A, B và C.
Lời giải:
a) Tam giác ABC là tam giác đều nên góc BAC = 60° => Góc AOB = 120°
Tương tự ta có góc AOC = 120°; góc COB = 120°
b) Vì Góc AOB = góc AOC = góc COB = 120°
=> Số đo cung AB = Số đo cung BC = Số đo cung AC = 240°
Bài tập 5: Cho đường tròn (O; 5cm) và điểm M sao cho đoạn thẳng OM = 10cm. Vẽ hai tiếp tuyến MA và MB của (O; 5cm). Tính số đo góc ở tâm do hai tia OA và OB tạo ra.
Lời giải:
Ta có:
Tam giác vuông MAO (vuông tại O) có: cos góc AOM = R/2R = 1/2 => Góc AOM = 60°.
Vì MA và MB là hai tiếp tuyến của (O) nên OM là tia phân giác của góc AOB => Góc AOB = 120°.
Bài tập trắc nghiệm
Câu 1: Cho hai tiếp tuyến tại tiếp điểm A và B của đường tròn tâm O cắt nhau tại M, biết AMB = 50°. Tìm số đo góc AMO và góc BOM?
A. Góc AMO = 35° ; góc MOB = 55°.
B. Góc AMO = 65° ; góc MOB = 25°.
C. Góc AMO = 25° ; góc MOB = 65°.
D. Góc AMO = 55° ; góc MOB = 35°.
Lời giải:
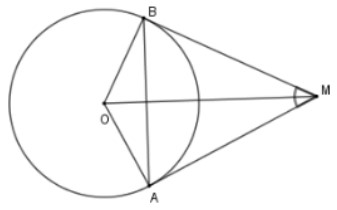
Ta có: Vì MA, MB là hai tiếp tuyến của đường tròn tâm O nên:
- OM là tia phân giác của góc AOB
- MO là tia phân giác của góc AMB hay góc AMO = 1/2 góc AMB = 50°/ 2 = 25°
Mà tam giác vuông OAM (vuông tại A) do có MA là tiếp tuyến
=> góc MOA = 90° − góc AMO = 65°
Mà OM là tia phân giác của góc AOB => góc MOB = góc MOA = 65°.
Vậy góc AMO = 25°; góc MOB = 65°
=>C là đáp án chính xác.
Câu 2: Cho đường tròn tâm O có hai tiếp tuyến tại tiếp điểm C và D cắt nhau tại điểm N, biết góc CND = 60°. Tìm số đo cung CD nhỏ và số đo cung CD lớn?
A. 150°; 210°.
B. 120°; 230°.
C. 120°; 240°.
D. 240°; 120°.
Lời giải
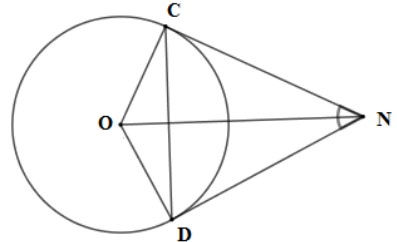
Xét tứ giác ODNC có:
Tổng 4 góc: COD + OCN + CND + ODN = 360°
=> Góc COD = 360° − góc OCN – góc ODN – góc CND = 360° – 90° – 90° – 60° = 120°
Từ đó suy ra: Số đo cung nhỏ CD là 120° ; số đo cung lớn CD là 360° – 120° = 240°
=>C là đáp án chính xác.
Xem full 30 câu trắc nghiệm về Góc ở tâm – Số đo cung tại đây:
Bài viết trên đây là toàn bộ kiến thức và các bài tập minh họa liên quan đến Góc ở tâm. Số đo cung. HOCMAI hy vọng rằng bài viết này sẽ giúp ích cho các em học sinh trong học tập và giải bài tập hình học Toán 9. Hẹn gặp lại các em học sinh ở các bài viết tiếp theo!


















