Một trong những kiến thức cực kỳ quan trọng trong chương trình toán hình học 9, Một số hệ thức về cạnh và góc trong tam giác vuông là nền tảng để các em học sinh có thể áp dụng để giải các dạng bài tập sau này. Kiến thức này không chỉ dừng lại ở chương trình lớp 9 mà nó còn xuất hiện xuyên suốt trong toán học cấp 3 và kỳ thi đại học. Trong bài viết gôm nay, HOCMAI sẽ giúp các bạn nắm vững các hệ thức và cách áp dụng để giải bài tập liên quan.
I. Các hệ thức về cạnh và góc trong tam giác vuông
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
- Cạnh huyền nhân với sin góc đối hoặc nhân với cosin góc kề;
- Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với cotang góc kề.
Ta có thể hiểu dễ hơn qua hình sau:
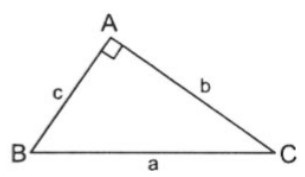
Trong tam giác vuông ABC (vuông tại A). Gọi a,b,c lần lượt là độ dài các cạnh BC, AD và AB. Ta có:
- Sin B = b/a => b = a.sin B và a = b/sin B
- Cos B = c/a => c = a.cos B và a = c/cos B
- Tan B = b/c => b = c.tan B và c = b/tan B
- Cot B = c/b => c = b.cot B và b =c/cot B
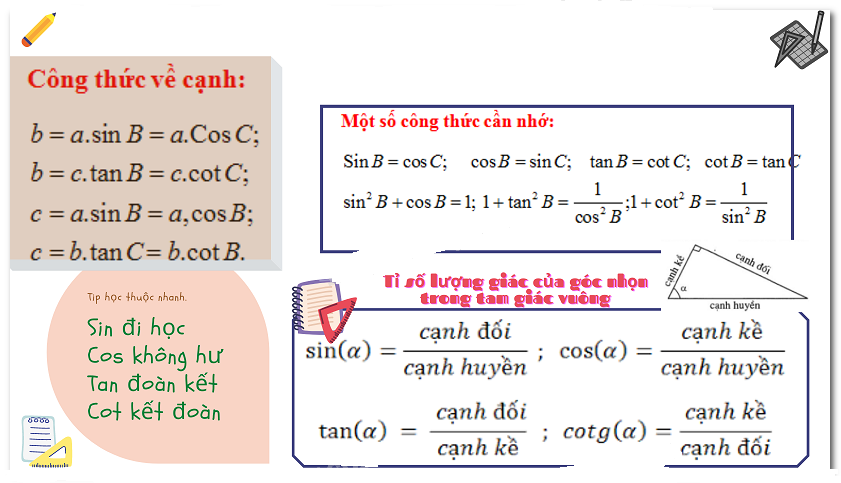
Tham khảo bảng Tỉ số lượng giác của góc nhọn trong tam giác vuông và Tips học thuộc nhanh sau đây:
II. Các dạng bài áp dụng một số hệ thức về cạnh và góc trong tam giác vuông
Dạng 1: Giải tam giác vuông
Đây là dạng bài tập yêu cầu chúng ta tìm độ dài các cạnh và số đo các góc của tam giác vuông dựa vào thông tin cho trước của bài toán.
Phương pháp giải: Để giải quyết dạng bài này, chúng ta cần áp dụng các hệ thức về các cạnh và góc của tam giác vuông.
Bài tập: Cho ΔABC vuông tại A có đường cao AH và góc B = . Tìm giá trị sao cho BH = 3CH.
Lời giải:
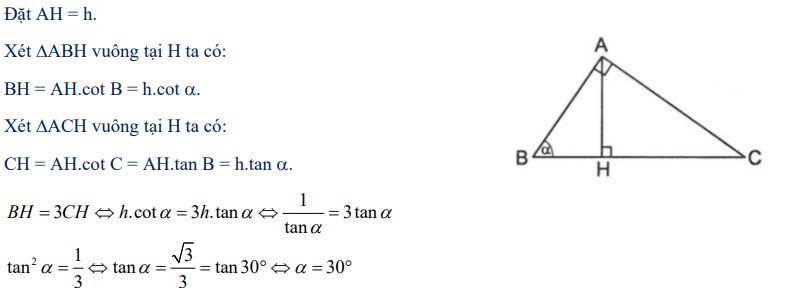
Nhận xét: Trong bài ta đã biểu diễn cạnh BH và cạnh CH theo đường cao AH và theo tỉ số lượng giác của góc . Từ mối quan hệ giữa cạnh BH và cạnh CH ta tìm được giá trị cần tìm của .
Bài tập 2: Cho ΔABC, cạnh BC cố định. Biết cạnh BC có độ dài là 4cm, Tổng độ dài cạnh AB và AC là 8cm. Tính GTLN của góc A.
Lời giải:

Nhận xét: Nhờ vẽ đường phân giác AD và các đường thẳng BH và CK vuông góc với AD mà ta tìm được mối quan hệ giữa các cạnh AB, AC với BH, CK; mối quan hệ giữa BH, CK với cạnh BC. Do đó cả 3 cạnh AB, AC và BC đều có sự liên hệ với nhau, từ đó tìm được góc A.
Dạng 2: Tính cạnh và góc của tam giác thường
Dạng bài tập này này không có sẵn tam giác vuông mà cần ta tạo ra tam giác vuông bằng việc kẻ thêm đường cao. Sau đó mới áp dụng các hệ thức về cạnh và góc trong tam giác vuông để tìm các góc và cạnh theo yêu cầu bài ra.
Phương pháp giải: Để giải quyết kiểu bài này, chúng ta phải làm xuất hiện tam giác vuông bằng cách kẻ thêm đường cao để dễ dàng áp dụng các hệ thức về cạnh và góc trong tam giác vuông.
Bài tập 1: Cho ΔABC với cạnh AB có độ dài là 5cm, cạnh BC = √39cm và cạnh CA = 7cm. Tìm số đo của góc A.
Lời giải:

Bài tập 2: Giải ΔABC, biết độ dài các cạnh AB, BC và CA lần lượt là 5cm, 7cm và 6cm (Chú ý: các số đo góc làm tròn đến độ).
Lời giải:

Nhận xét: Để giải được bài toán tam giác khi đã biết ba cạnh, chúng ta thường sử dụng định lý cosin.
Bài tập 3: Chứng minh định lý cosin: Trong một Δ nhọn, một cạnh có bình phương bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó với cosin của góc xen kẽ giữa của chúng.
Lời giải:

Nhận xét: Trong một tam giác nhọn, nếu biết được hai cạnh và góc xen kẽ giữa thì dựa vào định lý cosin ta có thể tìm được cạnh thứ ba.
Dạng 3: Toán ứng dụng thực tế
Phương pháp giải: Để giải quyết kiểu bài toán này, chúng ta sẽ sử dụng các hệ thức về cạnh và góc trong tam giác vuông để giải quyết các tình huống trong thực tế.
Bài tập 1: Một cột đèn đường cao 7m và có bóng đổ xuống trên mặt đất dài 4m. Hãy tìm góc (Số đo góc làm tròn đến phút) mà tia sáng mặt trời tạo ra với mặt đất (góc α trong hình vẽ).
Lời giải:
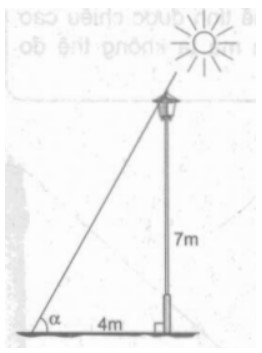
Áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có: tan góc α = 7/4 => α = 60°15′.
Bài tập 2: Một cầu trượt ở công viên có độ dốc là 28° và độ cao là 2,1 m. Tìm độ dài của mặt cầu trượt.
Lời giải:
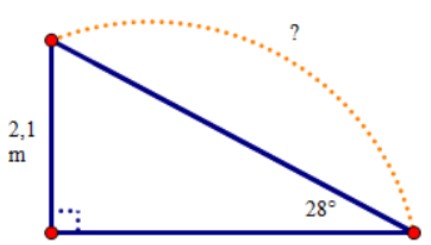
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
Độ dài mặt cầu trượt = 2,1/ sin 28° ≈ 4,47 m.
Dạng 4: Toán tổng hợp
Đây là dạng toán nâng cao tổng hợp cả 3 dạng trước. Để làm tốt dạng toán này, chúng ta cần vận dụng linh hoạt một số hệ thức về cạnh và góc trong tam giác vuông để giải đáp các yêu cầu bài toán đưa ra.
Bài tập: Cho tam giác ABC (vuông tại A) có AC>AB và đường cao AH. Gọi 2 điểm D, E lần là hình chiếu của điểm H trên cạnh AB và AC.
a) Chứng minh rằng: AD.AB = AE.AC và hai tam giác ABC và AED đồng dạng với nhau.
b) Cho biết độ dài BH = 2 cm và HC = 4,5 cm. Tìm độ dài đoạn thẳng DE; Số đo của góc ABC và Diện tích ΔADE.
Lời giải:
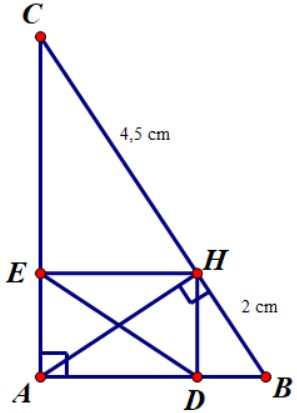
a) Vận dụng hệ thức lượng giữa cạnh và đường cao trong tam giác vuông để tìm mối liên hệ giữa tích AD.AB và AE.AC.
Xét tam giác vuông AHC, ta có: AH² = AE . AC (1)
Xét tam giác vuông AHB, ta có: AH² = AD . AB (2)
Từ (1) và (2) => AD.AB = AE.AC
Xét ΔABC và ΔAED có chung góc A = 90° và AD.AB = AE.AC (chứng minh trên).
=> ΔABC đồng dạng vơi Δ AED (cạnh – góc – cạnh)
b) Có 3 yêu cầu cần giải quyết:
+) Tìm độ dài đoạn thẳng DE
Theo câu a ta thấy tứ giác ADHE là một hình chữ nhật (vì có góc A, góc D và góc E đều là góc vuông) =>DE = AH (Hai đường chéo của hình chữ nhật) .
Mà AH là đường cao trong Δ vuông ABC nên áp dụng hệ thức lượng trong tam giác vuông ABC ta có:
AH² = HB.HC = 2 . 4,5 = 9 cm => AH= DE = 3 cm.
+) Tìm góc ABC:
Xét Δ vuông AHB, áp dụng hệ thức về cạnh và góc ta có:
tan góc ABC = AH/BH = 3/2 => Số đo của góc ABC ≈ 56°.
+) Tìm diện tích tam giác ADE.
Ta có ΔABC đồng dạng với Δ AED (chứng minh ở câu a) nên ta có thể sử dụng công thức tỉ số diện tích bằng bình phương tỉ số đồng dạng: S ΔADE / S ΔABC = (DE / BC)² = 27/13
Trong đó: S ΔABC = 1/2. AH. BC = 1/2 x 3 x 6,5 = 9,75 (cm²)
=> S ΔADE = 9,75 . 27/13 = 20,25 (cm²)
(Hết)
Bài viết tham khảo thêm:
Bài viết trên HOCMAI đã tổng hợp cho bạn Một số hệ thức về cạnh và góc trong tam giác vuông và các dạng bài tập liên quan. Hi vọng rằng qua bài viết này các em học sinh sẽ hiểu rõ hơn về bài học và ứng dụng để làm tốt bài tập Toán lớp 9 của mình. Chúc các em học tập tốt!





















