Góc tạo bởi tia tiếp tuyến và dây cung là kiến thức rất quan trọng trong chương trình hình học Toán 9. Đây là dạng bài thường xuất hiện trong các bài kiểm tra, kỳ thi cuối kỳ hay chuyển cấp. Trong bài viết này, HOCMAI sẽ giúp các em học sinh ôn tập kiến thức về định nghĩa, hệ thức và cách giải bài tập trắc nghiệm, tự luận của dạng toán này.
Bài viết tham khảo thêm:
A. Tóm tắt lý thuyết: Góc tạo bởi tia tiếp tuyến và dây cung
1. Định nghĩa
Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn và một cạnh là tia tiếp tuyến còn cạnh kia chưa dây cung của đường tròn đó.
Như vậy, góc tạo bởi tiếp tuyến và dây cung cần thỏa mãn các điều kiện sau:
- Đỉnh nằm trên đường tròn
- Một cạnh chứa tiếp điểm của đường tròn
- Cạnh còn lại sẽ chứa dây cung của đường tròn
Vậy chỉ cần thiếu ít nhất 1 trong 3 điều kiện trên thì góc đó không phải là góc tạo bởi tia tiếp tuyến và dây cung.
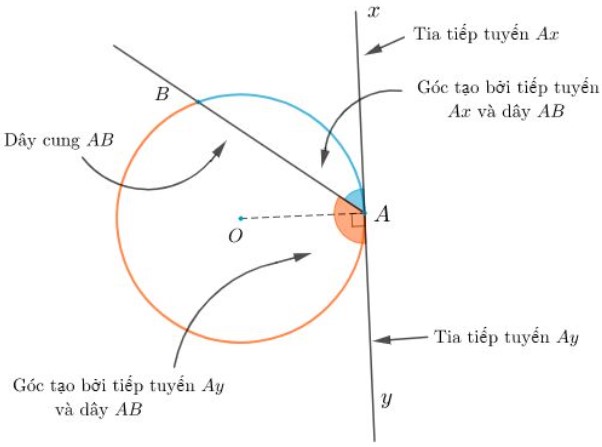
Ví dụ: Xét đường tròn (O) và Ax là tiếp tuyến của (O) tại A.
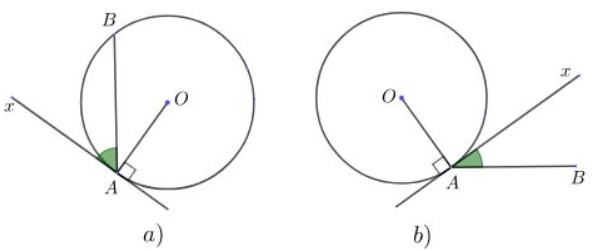
a) Góc BAx là góc tạo bởi tia tiếp tuyến và dây cung vì thỏa mãn 3 điều kiện:
- Đỉnh A ∈ đường tròn (O)
- Cạnh Ax là tiếp tuyến
- Cạnh AB là dây cung của đường tròn và góc BAx chắn cung nhỏ AB.
b) Góc BAx không phải là góc tạo bởi tia tiếp tuyến và dây cung vì:
- Đỉnh A ∈ đường tròn (O)
- Cạnh Ax là tiếp tuyến
- Cạnh AB không chứa dây cung dây cung của đường tròn
2. Định lý
Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng một nửa (1/2) số đo góc của cung bị chắn.
Chứng minh định lý:
Ta xét các trường hợp sau:
a) Tâm O nằm trên cạnh chưa dây cung AB (Hay dây AB là đường kính).
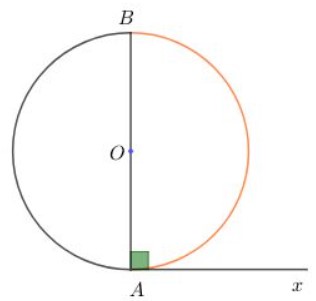
Vì O ∈ AB nên AB là đường kính
=> Góc BAx = 90° => Số đo cung AB = 180°.
Do đó: Góc BAx = 1/2 Số đo cung AB (ĐPCM).
b) Tâm O nằm phía bên ngoài góc BAx.
Kẻ đường cao AH và ký hiệu các góc như hình vẽ sau. Ta sẽ chúng minh góc BAx = 1/2 Số đo cung AB.
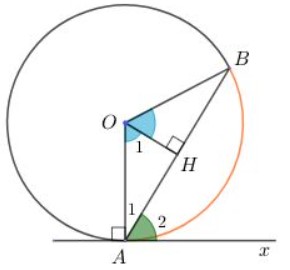
Vì OH ⊥ AB => góc OHA = 90° => góc O1 + góc A1 = 90° (1)
Vì Ax là tiếp tuyến của đường tròn (O) nên OA ⊥ Ax
=> góc A1 + góc A2 = 90° (2)
Từ (1) và (2) => góc O1 = góc O2
Lại có ΔOAB cân tại O nên đường cao OH đồng thời là phân giác của góc AOB
=> Góc AOB = 2 lần góc O1 = 2 lần góc A2
mặt khác, góc AOB là góc ở tâm chắn cung nhỏ BC nên góc AOB = số đo cung AB
=> 2 lần góc A2 = số đo cung AB => Góc A2 = 1/2 số đo cung AB (ĐPCM)
c) Tâm O nằm ở bên trong góc BAx.
Kẻ đường kính AC và ký hiệu các góc như hình dưới. Ta cần chỉ ra: góc BAx = 1/2 số đo cung ACB.
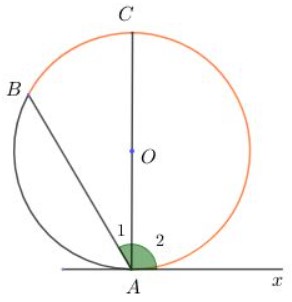
Khi đó góc BAx bao gồm hai góc A1 và góc A2.
Theo câu a, ta có góc A2 = 1/2 số đo cung AC
Lại có góc A2 là góc nội tiếp chắn cung nhỏ BC
=> Góc A1 = 1/2 số đo cung BC
Do đó:
Góc A1 + góc A2 = 1/2 số đo cung AC + 1/2 số đo cung BC
=> Góc BAx = 1/2 số đo cung ACB (ĐPCM).
Hệ quả
Trong một đường tròn, góc được tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
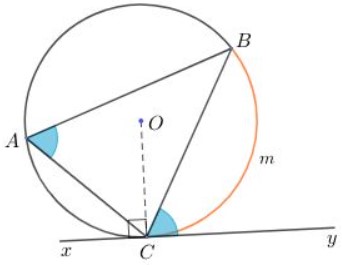
Góc BAC là góc nội tiếp chắn cung nhỏ BmC.
Góc BCy là góc tạo bởi tia tiếp tuyến Cy và dây cung CB chắn cung nhỏ Bmc.
Khi đó: góc BAC = góc BCy = 1/2 số đo cung BmC.
Bài tập Góc tạo bởi tia tiếp tuyến và dây cung
Bài tập trắc nghiệm
Câu 1: Cho một nửa đường tròn (O) và đường kính AB. Trên tia đối AB lấy điểm M. Vẽ tia tiếp tuyến MC với nửa đường tròn (O). Gọi điểm H là hình chiếu của điểm C trên AB. Tia CA là tia phân giác của góc nào?
A. Góc MCB
B. Góc MCO
C. Góc MCH
D. Góc CMB
Lời giải:
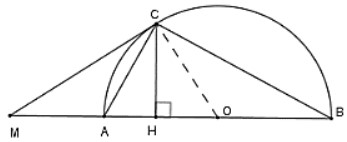
Xét xử đường tròn tâm O có: Góc MCA = Góc CBA (1)
Lại có góc ACB là góc vuông = 90° (Góc nội tiếp chắn nửa đường tròn)
=> Góc ACH = Góc CBA (2) (Cùng phụ với góc CAB)
Từ (1) và (2) => Góc MCA = Góc ACH => CA là tia phân giác của góc MCH
Vậy C là đáp án đúng
Câu 2: Cho một nửa đường tròn (O) và đường kính AB. Trên tia đối AB lấy điểm M. Vẽ tiếp tuyến với nửa đường tròn là MC. Gọi điểm H là hình chiếu của C trên AB. Giả sử OA = a; MC = 2a . Độ dài của CH là:
A. √5a/5
B. 2a/5
C. 2√5a/5
D. 3√5a/5
Lời giải:
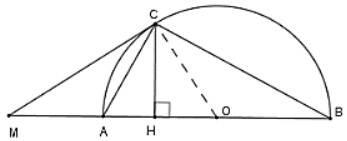
Có OA = OC = a
Xét tam giác vuông MCO vuông tại C (MC là tiếp tuyến của đường tròn)
=> MO = a√5
Xét tam giác MCO có:
Diện tích ΔMCO = 1/2CH.MO = 1/2 MC.CO
=> CH = (MC.CO)/MO = (a.2a)/a√5 = 2√5a/5
Vậy C là đáp án đúng
Câu 3: Cho đường tròn tâm (O), điểm M nằm ngoài đường tròn. Qua điểm M dựng tiếp tuyến MA đến đường tròn tâm O và dựng cát tuyến MBC. Đẳng thức nào sau đây là đúng ?
A. MA² = MB.MC
B. MB² = MA.MC
C. MC² = MA.MB
D. (1/MA)² = (1/MB)² + (1/MC)²
Lời giải:
Xét ΔMAB và ΔMCA có:
- Góc M chung
- Góc MAB = Góc MCA (Góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AB)
=> ΔMAB ∼ ΔMAC (góc – góc)
=> MA/MC = MB/MA => MA² = MB.MC
Vậy A là đáp án đúng
Câu 4: Cho đường tròn (O) và dây BC = √2R. Hai tiếp tuyến của đường tròn (O) tại tiếp điểm B và C cắt nhau tại A.
A. 45°
B. 30°
C. 60°
D. 75°
Lời giải:
Xét tam giác OBC có:
OB² + OC² = BC² = 2R² => Tam giác OBC vuông tại O => Góc BOC = 90°
Vì góc BOC là góc chắn cung BC => Số đo cung BC là 90°
Góc ABC là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC
=> Góc ABC = 1/2 số đo cung BC = 45°
Vậy A là đáp án đúng
Câu 5: Cho đường tròn (O; R) có dây BC không phải đường kính. Dựng hai tiếp tuyến tại điểm B và C và chúng cắt nhau tại A. Biết rằng góc ABC = 30°. Tính BC theo R?
A. BC = √3R
B. BC = √2R
C. BC = R
D. Đáp án khác
Lời giải:
Ta có:
Góc ABC là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC
=> Góc ABC = 1/2 số đo cung BC => Số đo cung BC = 60°
Góc BOC là góc nằm ở tâm chắn cung BC
=> Góc BOC = Số đo cung BC = 60°
Xét tam giác OBC có:
OB = OC = R và góc BOC = 60° => Tam giác OBC là tam giác đều
Do đó: BC = OB = OC = R
Vậy D là đáp án đúng
Bài tập tự luận
Bài 1: Cho điểm C thuộc nửa đường tròn tâm O đường kính AB. Từ điểm D thuộc đọan AO, kẻ đường thẳng vuông góc với AO và cắt AC, BC lần lượt tại 2 điểm E và F. Tiếp tuyến qua điểm C với nửa đường tròn cắt EF tại điểm M và cắt AB tại điểm N.
a) Chứng minh rằng M chính là trung điểm của EF.
b) Tìm vị trí của điểm C trên đường tròn (O) để ΔACN cân tại C.
Lời giải:
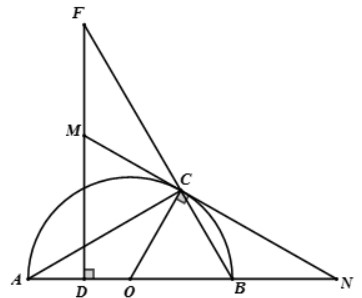
a) Ta có:
Góc MCA = 1/2 số đo cung AC (góc giữa tiếp tuyến và dây cung chắn cung AC) (1)
Lại có góc MEC = góc AED = 90° – góc EAD = 90° – 1/2 số đo cung BC = 1/2 số đo cung AC (2)
Từ (1) và (2) => Góc MCE = Góc MEC
=> ΔMEC cân tại M => MC = ME.
Chứng minh tương tự ta tìm được MC = MF.
=> ME = MF hay M chính là trung điểm của EF.
b) ΔACN cân tại C khi và chỉ khi góc CAN = góc CNA
Vì MN là tiếp tuyến với đường tròn (O) tại điểm C
=> OC ⊥ MN
=> Góc CNA = 90° – Góc COB = 90° – 2 lần Góc CAN
Góc CAN = Góc CNA ⇔ Góc CAN = 90° – 2 lần góc CAN ⇔ 3 lần góc CAN = 90°
=> Góc CAN = 30° => Số đo cung BC = 60°
Vậy ΔACN cân tại C khi C nằm trên nửa đường tròn (O) sao cho Số đo cung BC = 60°.
Bài 2: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại M. Kẻ đường thẳng d tiếp xúc với đường tròn tâm O tại điểm A và cắt (O’) tại điểm B và điểm C (Điểm B nằm giữa A và C). Gọi D là giao điểm của CM và đường tròn tâm O. Chứng minh rằng:
a) MA là phân giác của ∠BMD
b) MA² = MB.MD
Lời giải:
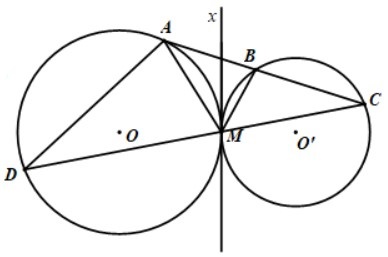
a) Kẻ tiếp tuyến chung của hai đường tròn (O) và (O’) là Mx
Ta có:
Góc BAM = Góc AMx (Góc giữa tia tiếp tuyến và dây cung cùng chắn cung AM của (O)).
Góc BMx = Góc BCM (Góc giữa tia tiếp tuyến và dây cung cùng chắn cung MB của (O’)).
Mặt khác Góc AMD = Góc MAB + Góc MCB (Góc AMD là góc ngoài của tam giác AMC)
=> Góc AMD = Góc AMx + Góc BMx = Góc BMA
=> MA là phân giác của Góc BMD (DPCM).
b) Xét ΔMAD và ΔBMD có:
- Góc AMD = Góc BMA (Theo chứng minh a)
- Góc ADM = Góc BAM
=> ΔMAD ∼ ΔMBA (góc – góc)
=> MA/MB = MD/MA hay MA² = MB.MD (DPCM).
Vậy là bài viết về Góc tạo bởi tia tiếp tuyến và dây cung đã kết thúc. HOCMAI mong rằng bài viết này sẽ giúp các em học sinh có thêm tài liệu bổ ích để ôn và luyện tập. Đừng quên truy cập vào hoctot.hocmai.vn thường xuyên để tìm kiếm những kiến thức bổ ích và cập nhật những bài viết mới nhất trên trang bạn nhé!





















