Đề cương ôn thi giữa học kì 2 toán 7 mới nhất

Bài viết dưới đây là bài Ôn thi giữa học kì 2 toán 7 dành cho các em học sinh khối 7 đang bắt đầu quá trình ôn thi của mình. Kỳ thi này tuy chỉ mới tổng hợp kiến thức của nửa học kỳ thôi nhưng các em tuyệt đối không nên chủ quan. Các em hãy chăm chỉ ôn luyện, tham khảo kiến thức và bài tập đã được tổng hợp trong bài viết trong quá trình ôn nhé!

 A. LÝ THUYẾT ÔN THI TOÁN LỚP 7 GIỮA HỌC KỲ 2

I. Đại số – Lý thuyết toán lớp 7 giữa học kỳ 2

Chương III: Thống kê

• Thu thập số liệu thống kê, tần số
• Bảng “tần số” các giá trị của dấu hiệu
• Biểu đồ
• Số trung bình cộng

Chương IV: Biểu thức đại số

• Khái niệm về biểu thức đại số. Giá trị của một biểu thứ đại số
• Đơn thức – Đơn thức đồng dạng

II. Hình học – Lý thuyết toán giữa kì 2 lớp  7

Chương II: Tam giác (tiếp theo)

• Luyện tập về ba trường hợp bằng nhau của tam giác
• Tam giác cân
• Định lý Py-ta-go
• Các trường hợp bằng nhau của tam giác vuông

Chương III: Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy của tam giác

• Quan hệ giữa góc và cạnh đối diện trong tam giác
• Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu

B. KIẾN THỨC TRỌNG TÂM TOÁN 7 GIỮA HỌC KÌ 2

I. Đại số – Tổng hợp kiến thức toán lớp 7 học kì 2

1. Thống kê

a) Dấu hiệu

Số liệu thống kê là những số liệu thu thập được từ việc điều tra một dấu hiệu. Ở đây, Mỗi số liệu chính là một giá trị của dấu hiệu.

Số các đơn vị điều tra bằng với số tất cả các giá trị (không nhất thiết phải khác nhau) của dấu hiệu.

b) Tần số

Chú ý:

Giá trị của dấu hiệu thường kí hiệu là x; tần số của giá trị thường kí hiệu là n.

Và N là kí hiệu cho số các giá trị và X là kí hiệu cho dấu hiệu.

c) Bảng tần số của dấu hiệu

– Từ bảng thu thập số liệu ban đầu ta có thể lập được bảng tần số.

Bảng “tần số” thường được tạo lập như sau:

+ Dựng một khung hình chữ nhật bao gồm hai dòng.

+ Dòng ở trên ghi các loại giá trị khác nhau của dấu hiệu theo thứ tự tăng lên dần.

+ Dòng bên dưới ghi các tần số tương ứng với mỗi giá trị đó.

– Bảng tần số giúp cho người điều tra dễ nhận xét về sự phân phối giá trị của dấu hiệu và tiện lợi trong việc tính toán về sau này.

Ta cũng có thể tạo lập bảng tần số theo hàng dọc.

d) Biểu đồ

* Biểu đồ đoạn thẳng:

+ Dựng một hệ trục tọa độ, trục hoành biểu diễn cho các giá trị x, trục tung biểu diễn cho tần số n (độ dài đơn vị trên ở hai trục có thể khác nhau).

+ Xác định các điểm trong biểu đồ có tọa độ là cặp số gồm: giá trị và tần số của nó (giá trị được viết trước, tần số được viết sau).

+ Nối mỗi điểm tạo được với điểm ở trên trục hoành có cùng một hoành độ.

* Biểu đồ hình chữ nhật:

+ Các đoạn thẳng có trong biểu đồ đoạn thẳng thì giờ được thay bằng hình chữ nhật.

* Biểu đồ hình quạt:

+ Đó chính là một hình tròn được chia ra thành các hình quạt mà trong đó góc ở tâm của các hình quạt có tỉ lệ với tần suất.

Chú ý: Tần suất f của một giá trị có thể tính theo công thức: f = n/N. Trong đó, f → tần số của giá trị đó, n → tần số của một giá trị,  N → số các giá trị. Chúng ta thường biểu diễn tần suất ở dưới dạng phần trăm.

e) Số trung bình cộng

+ Số trung bình cộng thường được sử dụng làm “đại diện” cho dấu hiệu, đặc biệt là khi muốn so sánh với các dấu hiệu cùng loại.

+ Khi những giá trị của dấu hiệu có khoảng chênh lệch rất lớn so với nhau thì không nên sử dụng số trung bình cộng làm “đại diện” của dấu hiệu.

+ Số trung bình cộng có thể không nằm trong dãy giá trị của dấu hiệu.

f) Mốt của dấu hiệu

+ Mốt của dấu hiệu chính là giá trị có tần số lớn nhất ở trong bảng “tần số”, kí hiệu là M0.

+ Có nhiều dấu hiệu có hai mốt hoặc có nhiều hơn.

2. Biểu thức đại số

a) Biểu thức đại số

Trong biểu thức đại số:

+ Biến số là những chữ đại diện cho một số tùy ý (chưa xác định).

+ Hằng số là những chữ đại diện cho một số xác định.

Để tính được giá trị biểu thức đại số ta nên thực hiện các bước sau:

+ Bước 1 – Thay biến bởi giá trị số đã cho trước (chú ý những trường hợp phải đặt số bên trong dấu ngoặc)

+ Bước 2 – Thực hiện những phép tính (lưu ý đến thứ tự thực hiện những phép tính: thực hiện phép lũy thừa, sau đến phép nhân, chia rồi sau đó mới là phép cộng trừ)

b) Đơn thức

+ Đơn thức là một biểu thức đại số chỉ gồm có 1 số, hoặc là 1 biến, hoặc là 1 tích giữa các biến và số.

+ Số 0 được tính là đơn thức không.

c) Đơn thức thu gọn

• Định nghĩa:

– Đơn thức thu gọn: là đơn thức chỉ gồm có tích của một số với các biến mà trong đó mỗi biến đều đã được nâng lũy thừa lên với số mũ nguyên dương. Số nói tới ở trên gọi là hệ số, phần còn lại thì được gọi là phần biến của một đơn thức thu gọn.

• Bậc của đơn thức:

+ Bậc của đơn thức thì có hệ số luôn khác 0 là tổng số mũ của tất cả các biến có bên trong đơn thức đó.

+ Số thực khác 0 là một đơn thức bậc không.

+ Số 0 thì được coi là một đơn thức không có bậc.

• Nhân hai đơn thức:

– Để nhân tích hai đơn thức, ta làm phép nhân các hệ số với nhau và phần biến với nhau.

d) Đơn thức đồng dạng

• Định nghĩa:

– Hai đơn thức đồng dạng khi hai đơn thức đó có hệ số khác 0 và có cùng biến. Các số khác 0 được coi là những đơn thức đồng dạng.

• Cộng, trừ đơn thức đồng dạng:

– Muốn cộng ( hoặc trừ) những đơn thức đồng dạng, ta cộng (hoặc trừ) phần hệ số với nhau và vẫn giữ nguyên phần biến.

II. Hình học – Đề cương ôn tập giữa kì 2 toán 7

1. Quan hệ giữa cạnh và góc đối diện trong tam giác:

Trong một tam giác, góc đối diện với cạnh lớn hơn thì là góc lớn hơn.

Tương tự, cạnh đối diện với góc lớn hơn thì là cạnh lớn hơn.

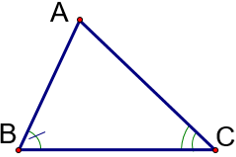
Tam giác ABC có: AC > AB ⇔ góc B > góc C

2. Quan hệ giữa đường vuông góc và đường xiên và hình chiếu

– Khái niệm của đường vuông góc, đường xiên và hình chiếu của đường xiên:

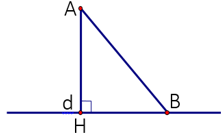
Lấy A ∉ d, kẻ đoạn AH ⊥ d, lấy B ∈ d. Khi đó:

+ Đoạn thẳng AH được gọi là đường vuông góc kẻ từ A đến điểm H nằm trên đường thẳng d.

+ Điểm H gọi là hình chiếu của điểm A trên đường thẳng d.

+ Đoạn thẳng AB được gọi là một đường xiên kẻ từ A đến đường thẳng d giao tại B.

+ Đoạn thẳng HB được gọi là hình chiếu của đường xiên AB trên đường thẳng d.

– Quan hệ giữa đường vuông góc với đường xiên: Trong các đường vuông góc và đường xiên kẻ từ một điểm ở bên ngoài một đoạn thẳng đến đường thẳng đó, đường vuông góc là đoạn thẳng ngắn nhất.

– Quan hệ giữa hình chiếu và đường xiên: Xét hai đường xiên được kẻ từ một điểm nằm bên ngoài một đường thẳng đến với đường thẳng đó, thì:

+ Đường xiên nào có số đo hình chiếu lớn hơn thì lớn hơn.

+ Đường xiên nào số đo lớn hơn thì có hình chiếu lớn hơn.

+ Nếu như hai đường xiên bằng nhau thì hai hình chiếu cũng bằng nhau và ngược lại, nếu hai hình chiếu mà bằng nhau thì hai đường xiên cũng bằng nhau.

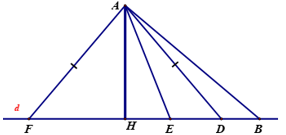
HB > HD > HE ⇔ AB > AD> AE

AD = AF ⇔ HD = HF

3. Quan hệ giữa ba cạnh trong một tam giác. Bất đẳng thức trong .tam giác

– Cùng một tam giác, tổng độ dài hai cạnh bất kì luôn luôn lớn hơn độ dài của cạnh còn lại.

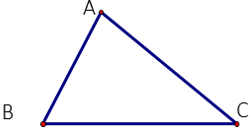
AB + AC > BC

AB + BC > AC

AC + BC > AB

– Hệ quả: Trong tam giác, hiệu của độ dài hai cạnh bất kì bao giờ cũng sẽ nhỏ hơn độ dài của cạnh còn lại.

|AC – BC | < AB

|AB – BC | < AC

|AC – AB| < BC

– Nhận xét: Trong tam giác, độ dài của một cạnh bao giờ cũng luôn nhỏ hơn tổng và lớn hơn hiệu của độ dài hai cạnh còn lại.

|AB – AC| < BC < AB + AC

Lưu ý: ta chỉ cần so sánh độ dài lớn nhất với cả tổng của độ dài hai cạnh còn lại, hoặc so sánh độ dài nhỏ nhất với cả hiệu của độ dài hai cạnh còn lại.

4. Tính chất của ba đường trung tuyến trong tam giác

– Đoạn thẳng AM nối từ đỉnh A của tam giác ABC với điểm M là trung điểm của cạnh BC, chính là đường trung tuyến của tam giác ABC. Đôi khi đoạn thẳng AM cũng được cho là đường trung tuyến của tam giác ABC. Mỗi tam giác thì đều có ba đường trung tuyến.

– Tính chất: Ba đường trung tuyến của một tam giác cùng giao qua một điểm (điểm đó được gọi là điểm trọng tâm). Điểm đó cách mỗi đỉnh một khoảng bằng 2/3 so với độ dài của đường trung tuyến đi qua đỉnh/điểm ấy.

– Ở trong một tam giác cân, hai đường trung tuyến tương ứng với hai cạnh bên thì chúng bằng nhau.

– Nếu một tam giác có hai đường trung tuyến bằng nhau thì kết luận rằng tam giác đó cân.

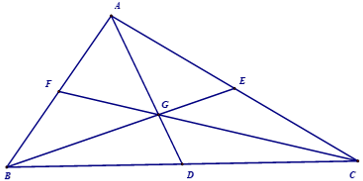
– Ba đường trung tuyến của một tam giác cùng giao qua một điểm. Điểm đó cách mỗi đỉnh của tam giác một khoảng bằng 2/3 độ dài của đường trung tuyến đi qua đỉnh ấy:

G là điểm trọng tâm của tam giác ABC như trong hình vẽ.

5. Tính chất của tia phân giác của một góc

– Điểm nằm ở trên tia phân giác của một góc thì nó sẽ cách đều hai cạnh của góc đó.Điểm nằm ở bên trong một góc và cách đều hai cạnh của góc đó thì nó nằm ở trên tia phân giác của góc đó.

– Tập hợp những điểm nằm ở bên trong một góc và cách đều với hai cạnh của góc đó sẽ tạo thành tia phân giác của góc đó.

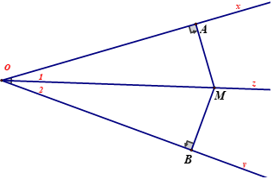
Oz là phân giác góc xOy, ta có:

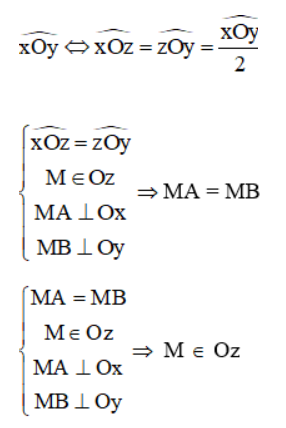
6. Tính chất ba đường phân giác trong tam giác

– Trong tam giác ABC ở bên dưới, tia phân giác của góc BAC giao với cạnh BC tại điểm M, khi đó đoạn thẳng AM chính là đường phân giác trong tam giác ABC (đôi khi ta cũng thường gọi đoạn thẳng AM là đường phân giác trong/của tam giác)

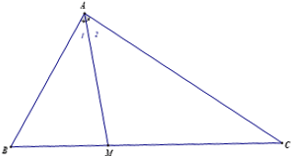
Tam giác ABC: góc A1 = góc A2 ⇒ AM là đường phân giác của góc BAC.

– Tính chất: Ở trong một tam giác cân, đường phân giác xuất phát từ đỉnh đồng thời chính là đường trung tuyến ứng với cạnh đáy.

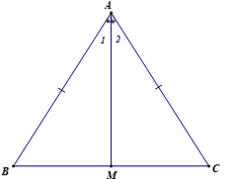
Tam giác ABC có: AB = AC; góc A1 = góc A2 ⇒BM = MC

– Tính chất của ba đường phân giác của tam giác: Ba đường phân giác trong một tam giác cùng giao qua một điểm. Điểm này cách đều với ba cạnh của tam giác đó.

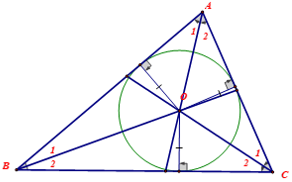
– Nếu tam giác có một đường trung tuyến đồng thời cũng chính là đường phân giác thì tam giác đó chắc chắn là một tam giác cân.

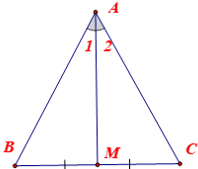
Tam giác ABC có: BM = MC; góc A1 = góc A2 ⇒ tam giác ABC cân.

7. Tính chất của đường trung trực của một đoạn thẳng

– Điểm nằm ở trên đường trung trực của một đoạn thẳng thì sẽ cách đều hai mút của đoạn thẳng ấy.

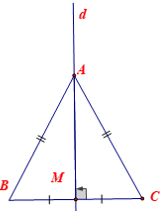
Ta có: d ⊥ BC tại M; MB = MC ⇒ d là đường trung trực của đoạn BC, A ∈ d ⇒ AB = AC

– Điểm cách đều với hai mút của một đoạn thẳng thì sẽ nằm trên đường trung trực của đoạn thẳng ấy. Tập hợp những điểm cách đều hai mút của một đoạn thẳng chính là đường trung trực của đoạn thẳng ấy.

8. Tính chất ba đường trung trực của tam giác

– Ở trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó.

– Ở trong một tam giác cân, đường trung trực của cạnh đáy đồng thời cũng chính là đường trung tuyến ứng với cạnh này.

– Tính chất của ba đường trung trực của tam giác: Ba đường trung trực của một tam giác cùng giao tại một điểm. Điểm này luôn cách đều ba đỉnh của tam giác đó.

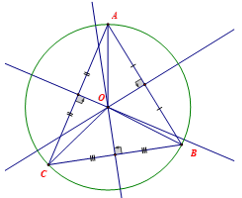
O là giao điểm của những đường trung trực trong ΔABC ⇔ OA = OB = OC

– Nếu trong tam giác có một đường trung tuyến đồng thời cũng là đường trung trực ứng với cùng một cạnh thì tam giác đó chắc chắn là một tam giác cân.

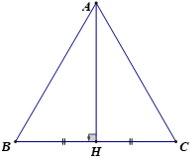
Có HB = HC và AH ⊥ BC ⇒ ΔABC cân tại A

9. Tính chất của ba đường cao trong tam giác

– Đường cao của tam giác: Ở trong một tam giác, đoạn thẳng vuông góc kẻ từ một đỉnh đến với cạnh đối diện gọi là đường cao của tam giác ấy. Đôi khi ta cũng có thể gọi đoạn thẳng AI là đường cao của tam giác.

– Tính chất của ba đường cao trong tam giác: Ba đường cao trong một tam giác cùng giao tại một điểm. Điểm này được gọi là trực tâm của tam giác.

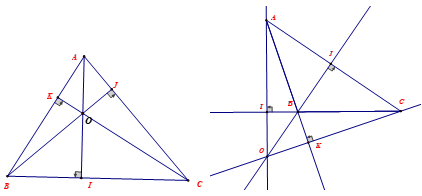
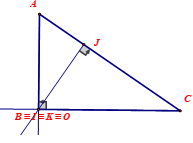
Lưu ý: Trực tâm của một tam giác nhọn nằm ở bên trong tam giác. Trực tâm của một tam giác vuông trùng với đỉnh góc vuông. Trực tâm của một tam giác tù nằm ở bên ngoài của tam giác.

Tính chất của tam giác cân: Ở trong một tam giác cân, đường trung trực tương ứng với cạnh đáy đồng thời cũng là một đường cao, đường trung tuyến và đường phân giác cùng xuất phát từ đỉnh đối diện của cạnh đó.

+) Nhận xét:

– Ở trong một tam giác, nếu hai trong bốn loại đường đặc biệt (đường phân giác | đường trung tuyến | đường cao |đường trung trực ứng với cạnh đối diện tại đỉnh này) trùng nhau thì tam giác đó chính là một tam giác cân.

– Ở trong một tam giác đều, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh, trọng tâm là bốn điểm trùng nhau.

C. ĐỀ CƯƠNG GIỮA KÌ 2 TOÁN 7 – CÁC DẠNG TOÁN THƯỜNG GẶP

Dạng 1: Toán về thống kê

Dạng 2: Toán về biểu thức đại số, đơn thức

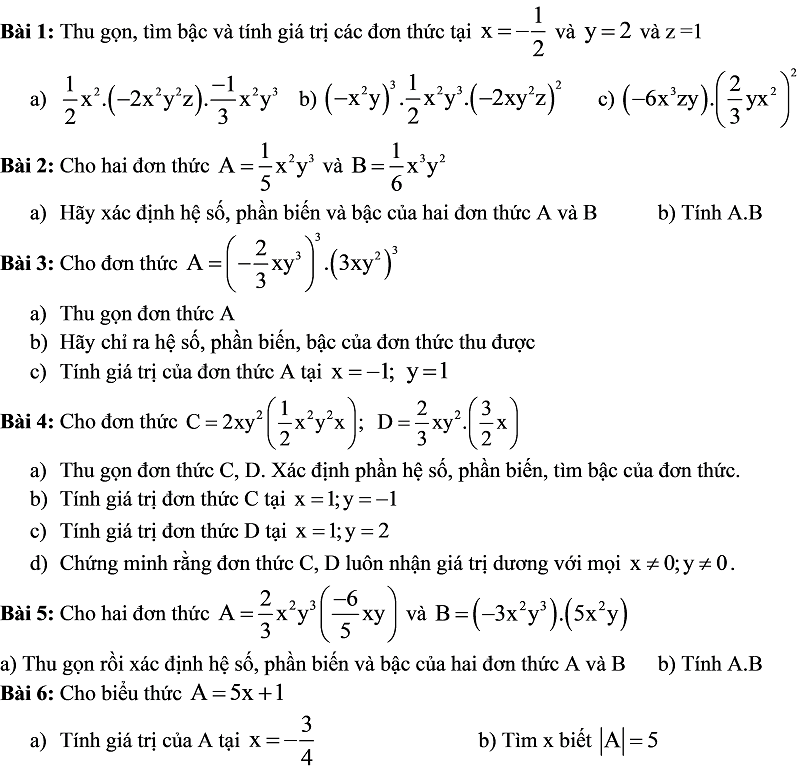
Dạng 3: Các bài toán hình học

Dạng 4: Toán nâng cao – Đề kiểm tra giữa kì 2 toán 7

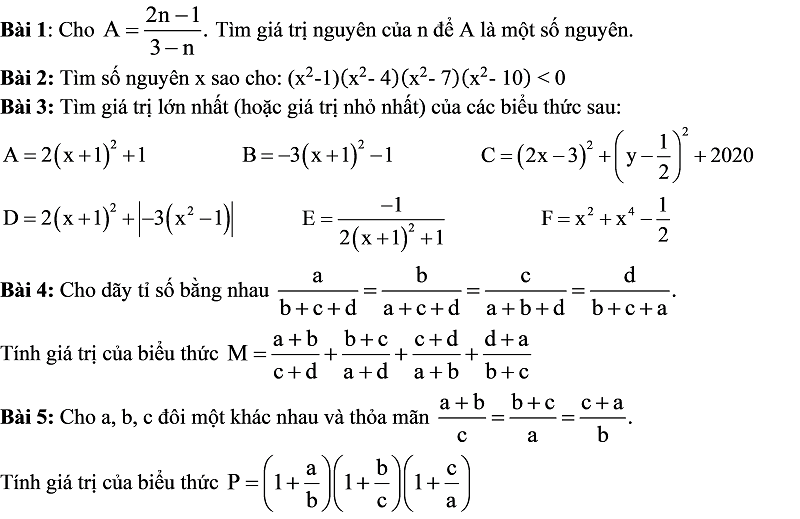
D. ĐỀ THI GIỮA KÌ 2 TOÁN 7 CÓ ĐÁP ÁN

Trên đây là bài Đề cương ôn thi giữa học kì 2 toán 7. Các em học sinh hãy tham khảo và ôn luyện thật chăm chỉ để đạt được kết quả tốt nhất nhé. Các em có thể tham khảo thêm nhiều bài học hay và bổ ích tại website hoctot.hocmai.vn.