Như các em học sinh thân mến đã biết, hình tứ giác là một trong những kiểu hình học thường gặp nhất trong các bài toán. Tư giác còn được phân ra làm rất nhiều loại tứ giác đặc biệt khác nhau. Ở bài viết tổng hợp dạng bài về tứ giác này, HOCMAI đã biên soạn đầy đủ tất cả định nghĩa, tính chất, dấu hiệu nhận biết và cách thức chứng minh của những tứ giác đặc biệt đó. Nào chúng ta hãy cùng mở vở ra và cùng nhau học bài ngay thôi nào các em học sinh!
A. LÝ THUYẾT VỀ TỨ GIÁC
I. Định nghĩa hình tứ giác
Hình tứ giác là một đa giác gồm có bốn đỉnh và bốn cạnh. Trong đó, không có bất kỳ đoạn thẳng nào cùng nhau nằm trên một đường thẳng.
Tứ giác có thể là tứ giác đơn khi không có cặp cạnh đối nào cắt nhau hoặc là tứ giác kép (có hai cặp cạnh đối cắt nhau). Tứ giác đơn có thể là ở dạng lồi hoặc ở dạng lõm.
II. Tính chất hình tứ giác
Tứ giác có hai tính chất cơ bản như sau:
Tính chất 1: Tính chất hình chéo
Trong một tứ giác lồi thì hai đường chéo cắt nhau tại một điểm thuộc miền bên trong của tứ giác đó.
Ngược lại, nếu như một tứ giác có hai đường chéo giao nhau tại một điểm thuộc miền bên trong của nó thì tứ giác ấy chắc chắn sẽ là tứ giác lồi.
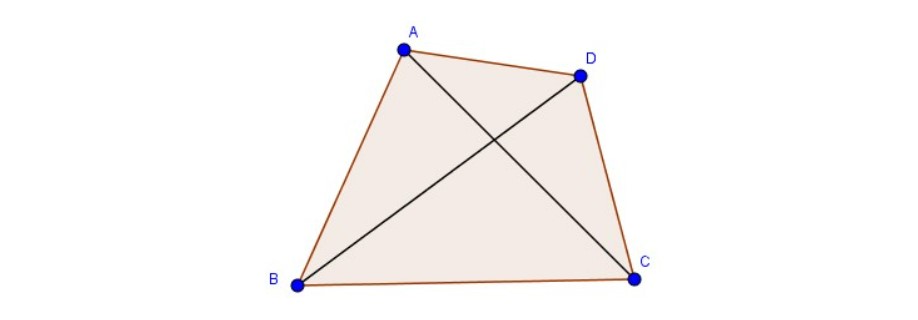
Tính chất 2: Tính chất góc của hình tứ giác
Tổng bốn góc trong của tứ giác bằng 360 độ.
III. Cách nhận biết các hình tứ giác
Có 4 dạng tứ giác thường gặp đó là:
Dạng 1: Tứ giác đơn.
Tứ giác đơn là bất kỳ tứ giác nào không có cạnh nào giao nhau.
Dạng 2: Tứ giác lồi
Tứ giác lồi là kiểu tứ giác mà tất cả các góc trong nó đều có số đo nhỏ hơn 180° và hai đường chéo đều nằm ở bên trong tứ giác. Hay nói một cách dễ hiểu hơn thì tứ giác lồi là tứ giác luôn nằm gọn trong một nửa mặt phẳng có chứa bất kỳ cạnh nào.
Dạng 3: Tứ giác lõm.
Tứ giác lõm là kiểu tứ giác mà chứa một góc trong có số đo lớn hơn 180 độ và một trong hai đường chéo sẽ là nằm bên ngoài tứ giác.
Dạng 4: Tứ giác không đều.
Tứ giác không đều là kiểu tứ giác mà nó không có bất kỳ cặp cạnh nào song song với nhau. Tứ giác không đều thường được dùng để đại diện cho tứ giác lồi nói chung (không phải là tứ giác đặc biệt).
Không chỉ có 4 dạng tứ giác thường gặp vừa nêu trên mà hình tứ giác còn có những dạng đặc biệt thường gặp như ở bên dưới đây.
IV. Hình tứ giác đặc biệt
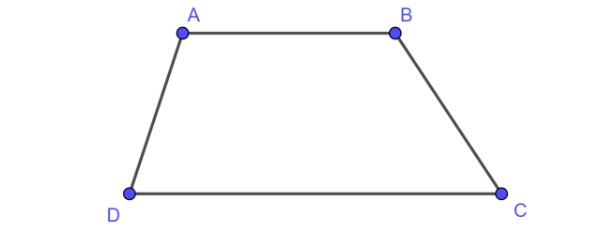
1. Dạng 1: Dấu hiệu nhận biết tứ giác là hình thang
Hình thang là hình tứ giác có ít nhất một cặp cạnh đối song song với nhau.
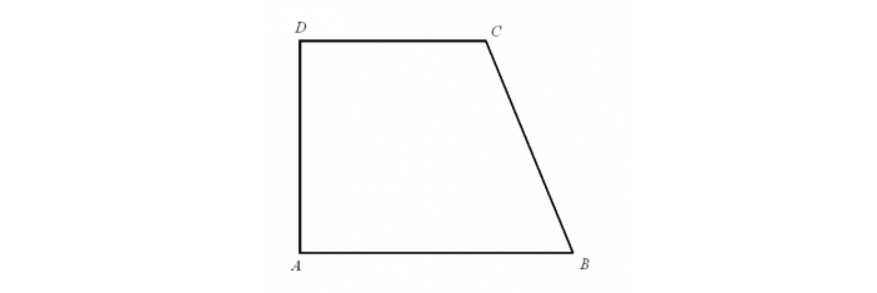
2. Dạng 2: Dấu hiệu nhận biết tứ giác là Hình thang vuông
Hình thang vuông là hình thang có ít nhất một góc trong là góc vuông.
Dấu hiệu nhận biết:
– Tứ giác mà có ít nhất một cặp cạnh đối song song và một góc vuông là hình thang vuông.
– Tứ giác mà có ít nhất hai góc vuông là hình thang vuông.
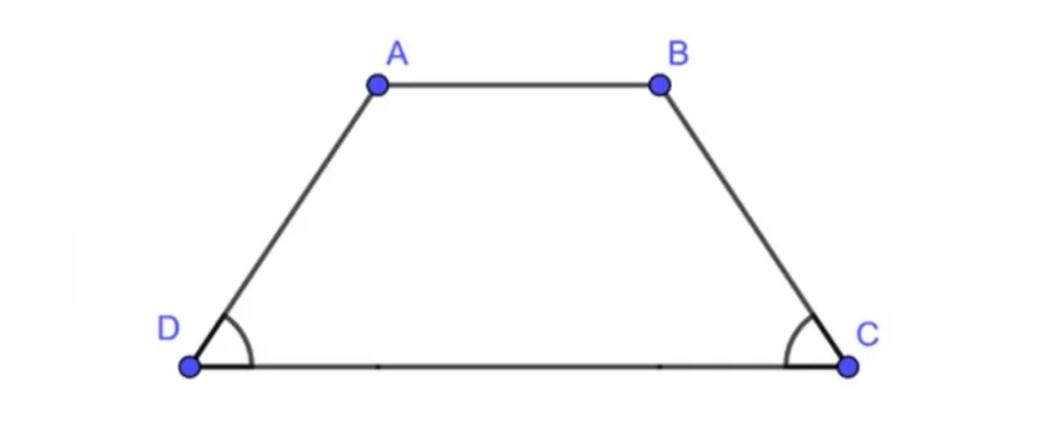
3. Dạng 3: Dấu hiệu nhận biết tứ giác là Hình thang cân
Không chỉ mỗi hình thang được cho là dạng đặc biệt của tứ giác mà hình thang cân cũng vậy, cũng được coi là một trong số dạng tứ giác đặc biệt.
Hình thang cân là hình thang có hai góc kề cùng một cạnh đáy bằng nhau và hai đường chéo bằng nhau.
Dấu hiệu nhận biết:
– Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân.
– Hình thang có hai đường chéo bằng nhau là hình thang cân.
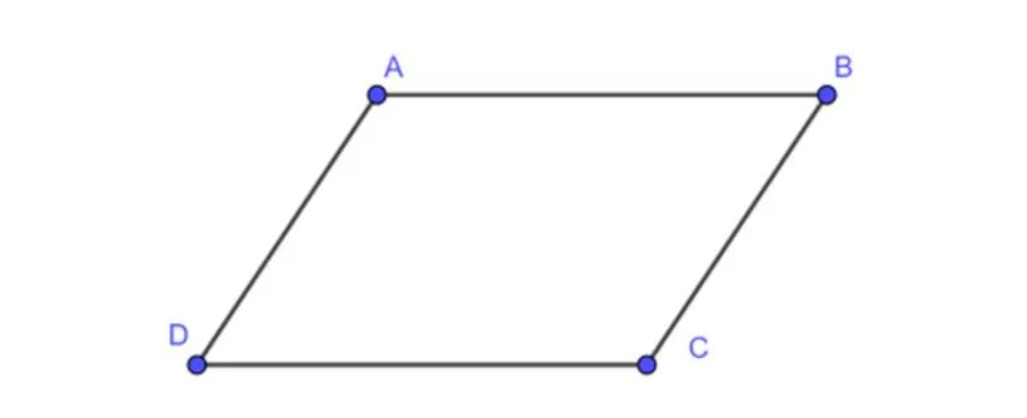
4. Dạng 4: Dấu hiệu nhận biết tứ giác là Hình bình hành
Hình bình hành là hình tứ giác có hai cặp cạnh đối song song với nhau. Trong hình bình hành thì các góc đối bằng nhau, các cạnh đối bằng nhau, đường chéo cắt nhau tại trung điểm của mỗi đường. Hình bình hành được cho là trường hợp đặc biệt của hình thang.
Dấu hiệu nhận biết:
– Tứ giác có hai cặp cạnh đối song song với nhau thì là hình bình hành.
– Tứ giác có các cạnh đối bằng với nhau thì là hình bình hành.
– Tứ giác có các góc đối bằng với nhau thì là hình bình hành.
– Tứ giác có một cặp cạnh đối song song với nhau và bằng nhau thì là hình bình hành.
– Tứ giác có hai đường chéo giao nhau tại trung điểm của mỗi đường thì là hình bình hành.
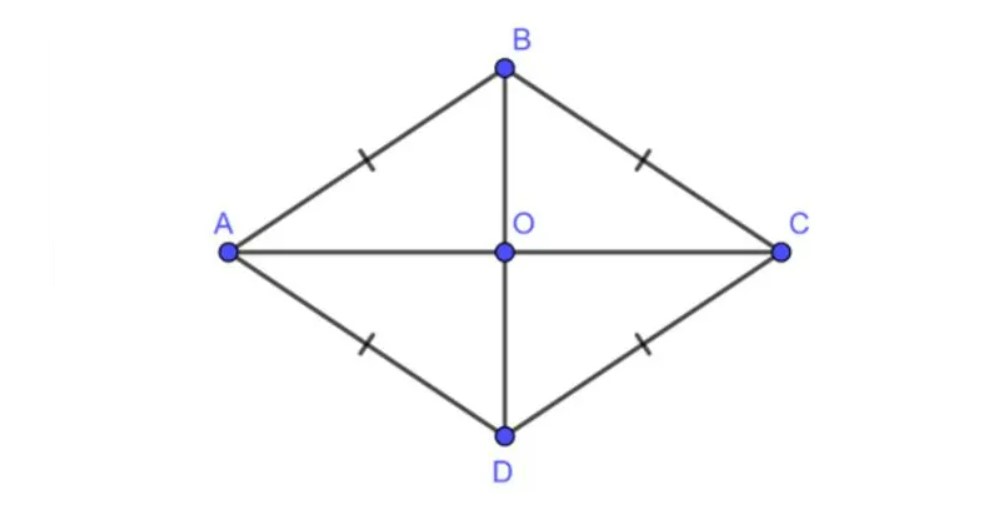
5. Dạng 5: Dấu hiệu nhận biết tứ giác là Hình thoi
Hình thoi cũng là một dạng hình tứ giác đặc biệt bởi vì hình thoi là hình tứ giác có bốn cạnh bằng nhau.
Dấu hiệu nhận biết:
– Tứ giác có bốn cạnh bằng với nhau thì là hình thoi.
– Tứ giác có hai đường chéo là đường phân giác của cả bốn góc trong thì là hình thoi.
– Tứ giác có hai đường chéo là đường trung trực của mỗi đường thì là hình thoi
– Hình bình hành có hai cạnh kề bằng với nhau thì là hình thoi.
– Hình bình hành có hai đường chéo vuông góc với nhau thì là hình thoi.
– Hình bình hành có một đường chéo là đường phân giác của một góc trong thì là hình thoi.
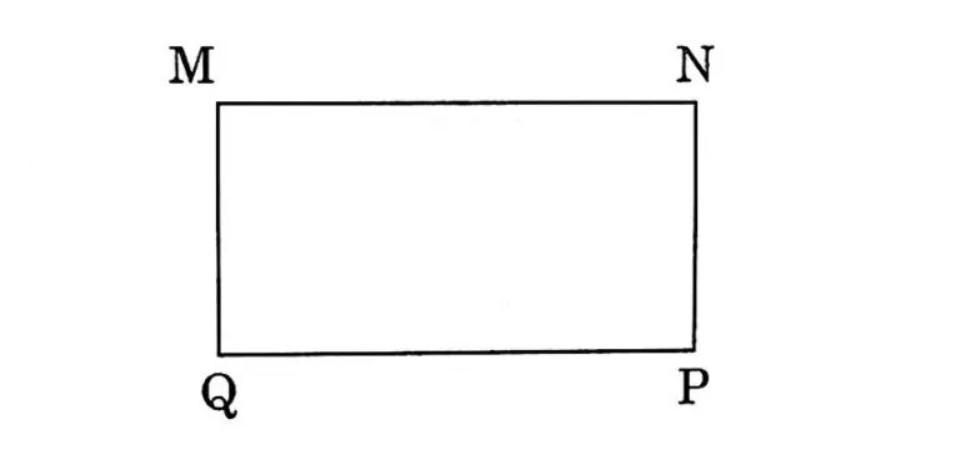
6. Dạng 6: Dấu hiệu nhận biết tứ giác là Hình chữ nhật
Hình chữ nhật là một dạng hình tứ giác đặc biệt vì hình chữ nhật là hình tứ giác có bốn góc vuông, một điều kiện tương đương khác là hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Dấu hiệu nhận biết:
– Tứ giác có ba góc bằng 90 độ là hình chữ nhật.
– Hình thang cân có một góc bằng 90 độ là hình chữ nhật.
– Hình bình hành có một góc bằng 90 độ là hình chữ nhật.
– Hình bình hành có hai đường chéo bằng với nhau là hình chữ nhật.
7. Dạng 7: Dấu hiệu nhận biết tứ giác là Hình vuông
Hình vuông là một tứ giác có bốn góc bằng 90 độ và bốn cạnh bằng nhau. Hình vuông có các đường chéo bằng nhau và vuông góc tại trung điểm, có các cạnh đối song song. Một tứ giác được coi là một hình vuông khi và chỉ khi nó vừa là một hình thoi vừa là một hình chữ nhật (bốn góc bằng nhau và bốn cạnh bằng với nhau).
Dấu hiệu nhận biết:
– Hình chữ nhật có hai cạnh kề bằng với nhau là hình vuông.
– Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
– Hình thoi có một góc bằng 90 độ là hình vuông.
– Hình thoi có hai đường chéo bằng với nhau là hình vuông.
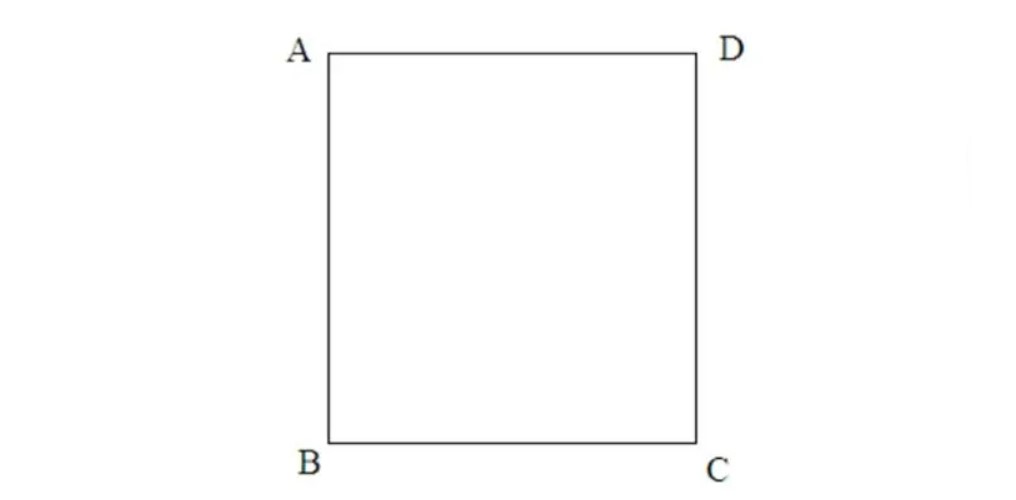
B. PHƯƠNG PHÁP CHỨNG MINH TỨ GIÁC ĐẶC BIỆT
I. CHỨNG MINH TỨ GIÁC LÀ HÌNH THANG
Cách 1: Chứng minh tứ giác đó có một cặp đối song song
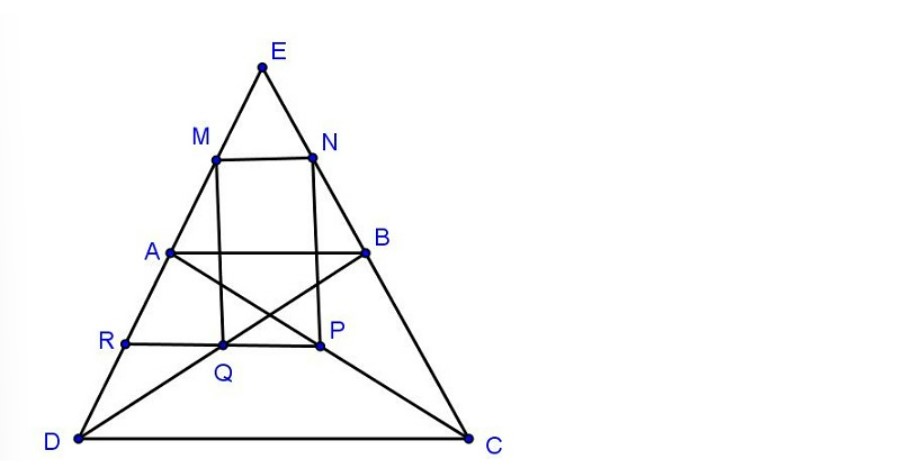
Ví dụ: Cho hình thang ABCD có cạnh AB và cạnh CD song song với nhau. Gọi E là giao điểm của 2 đường thẳng AD và đường thẳng BC. Gọi M, N, Q, P theo thứ tự là các trung điểm của các đoạn thẳng AE, BE, BD, và AC. Chứng minh rằng tứ giác MNPQ là một hình thang.
Hướng dẫn giải bài:

Cách 2: Chứng minh tứ giác đó có tổng hai góc kề một cạnh bằng 180 độ.
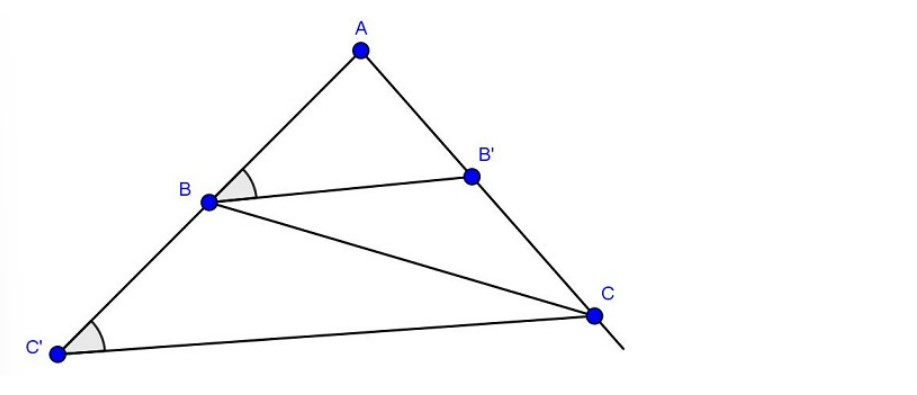
Ví dụ: Cho tam giác ABC. Trên AC lấy một điểm B’ sao cho độ dài AB và AB’ bằng nhau và trên AB lấy một điểm C’ sao cho độ dài AC’ và AC bằng nhau. Chứng minh rằng tứ giác BB’CC’ là một hình thang.
Hướng dẫn giải bài:

II. CHỨNG MINH TỨ GIÁC LÀ HÌNH THANG CÂN
Cách 1: Chứng minh tứ giác đó có hai cạnh song song và hai góc kề đáy bằng nhau.
Cách 2: Chứng minh tứ giác đó có hai cạnh song song và hai đường chéo có độ dài bằng nhau.
Cách 3: Chứng minh tứ giác đó có hai góc kề đáy bằng nhau và hai đường chéo có độ dài bằng nhau.
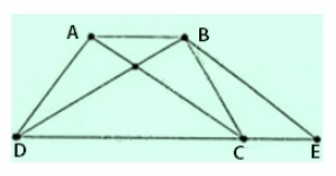
Ví dụ: Cho hình thang ABCD có cạnh AB song song với cạnh CD, độ dài của AD bằng với độ dài của BC. Qua điểm B kẻ đường thẳng song song với AC, cắt đoạn thẳng DC tại điểm E. Hãy chứng minh rằng:
a) Tam giác BDE là một tam giác cân.
b) Tam giác ACD và tam giác BDC có kích cỡ bằng nhau.
c) Hình thang ABCD là một hình thang cân.
Hướng dẫn giải bài:

III. CHỨNG MINH TỨ GIÁC LÀ HÌNH BÌNH HÀNH
Cách 1: Chứng minh tứ giác có các góc đối bằng nhau:
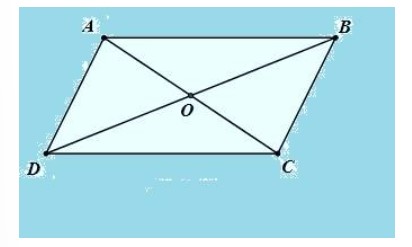
Ví dụ: Cho tứ giác ABCD có tam giác ABC và tam giác ADC có kích cỡ bằng nhau, tam giác BAD và tam giác BCD có kích cỡ bằng nhau. Chứng minh rằng tứ giác ABCD là hình bình hành.
Hướng dẫn giải bài:

Cách 2: Chứng minh tứ giác có một cặp cạnh đối song song và bằng nhau.
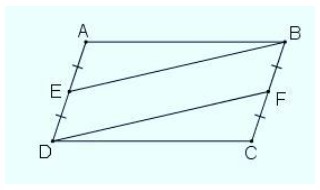
Ví dụ: Cho một hình bình hành ABCD, gọi E là trung điểm của cạnh AD còn F là trung điểm của cạnh BC. Hãy chứng minh rằng tứ giác BEDF là một hình bình hành.
Hướng dẫn giải bài:

Cách 3: Chứng minh tứ giác có các cạnh đối bằng với nhau:
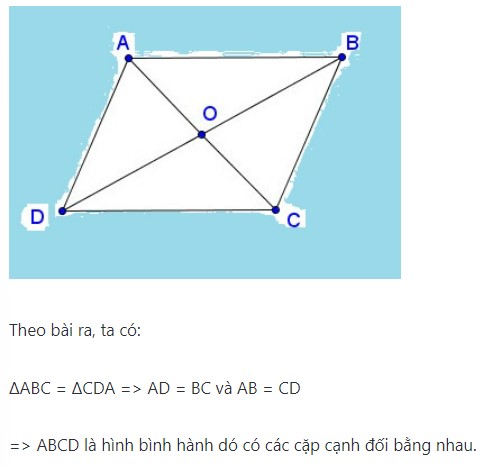
Ví dụ: Cho tứ giác ABCD có tam giác ABC và tam giác CDA có kích cỡ bằng nhau. Em hãy chứng minh rằng tứ giác ABCD là hình bình hành.
Hướng dẫn giải bài:
Cách 4: Chứng minh tứ giác có các cạnh đối song song
Ví dụ: Cho hình tứ giác ABCD có E, F, H, G theo thứ tự lần lượt là trung điểm của các cạnh AB, BC, DA, CD. Vậy tứ giác EFGH là hình gì và tại sao?
Hướng dẫn giải bài:

Cách 5: Chứng minh tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường
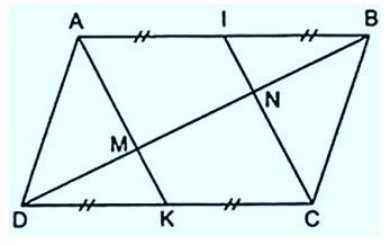
Ví dụ: Cho hình bình hành ABCD. Gọi điểm I và điểm K lần lượt là trung điểm của cạnh AB và cạnh CD. Đường chéo BD cắt đoạn AK vầ AI lần lượt tại điểm M và điểm N. Chứng minh rằng đoạn AK song song với đoạn CI và độ dài đoạn DM, MN, NB là bằng nhau.
Hướng dẫn giải bài:

IV. CHỨNG MINH TỨ GIÁC LÀ HÌNH THOI
Cách 1: Chứng minh tứ giác có hai đường chéo là trung trực của nhau
Ví dụ: Cho hình thang ABCD có độ dài AB bằng độ dài AC. Kéo dài đường trung tuyến AM của tam giác ABC sao cho độ dài AM độ dài ME bằng nhau. Chứng minh tứ giác ABEC là một hình thoi.
Hướng dẫn giải bài:
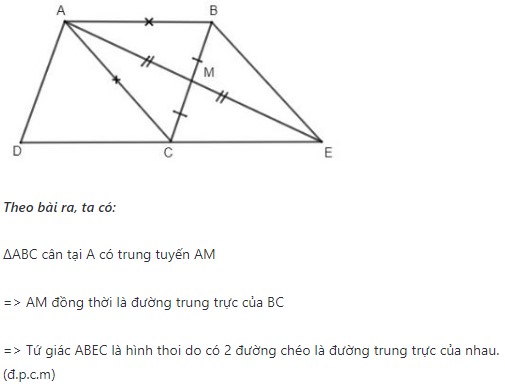
Cách 2: Chứng minh tứ giác có bốn cạnh bằng với nhau
Ví dụ: Hãy chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi.
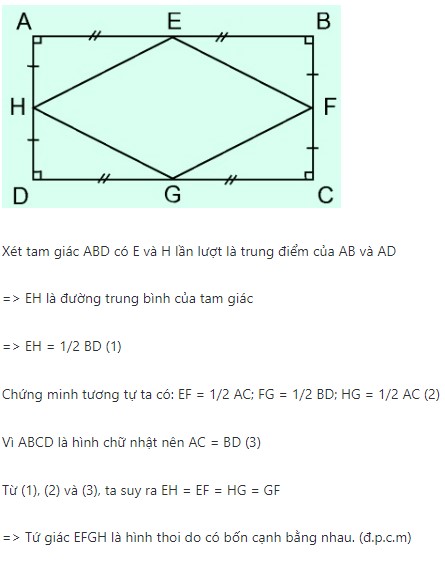
Cách 3: Chứng minh tứ giác là hình bình hành có hai đường chéo vuông góc.
Ví dụ: Gọi O là giao điểm của hai đường chéo trong một hình bình hành ABCD. Chứng minh rằng giao điểm các đường phân giác trong các tam giác AOB, BOC, DOA và COD là đỉnh của một hình thoi.
Hướng dẫn giải bài:
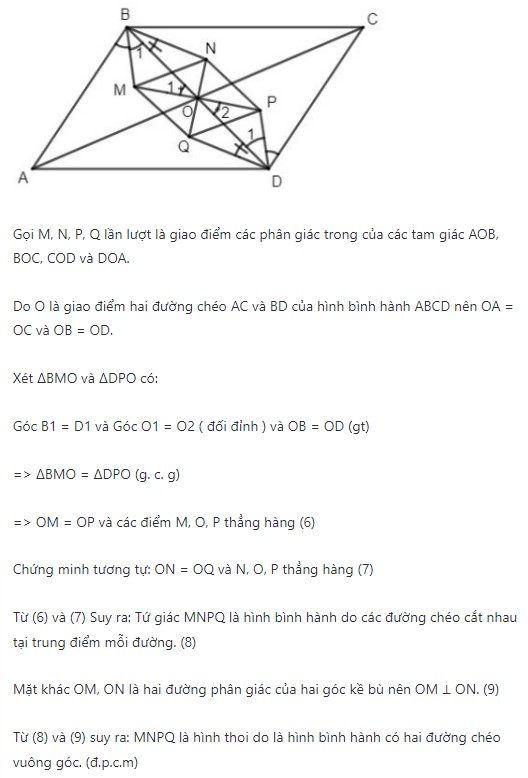
Cách 4: Chứng minh tứ giác là hình bình hành có hai cạnh kề bằng với nhau
Ví dụ: Cho tam giác ABC, lấy các điểm D và điểm E theo thứ tự lần lượt trên các cạnh AB và AC sao cho độ dài của BD và CE là bằng nhau. Gọi M, N, K. I lần lượt là trung điểm của BE, CD, BC, DE. Hãy chứng minh rằng tứ giác IMNK là một hình thoi.
Hướng dẫn giải bài:
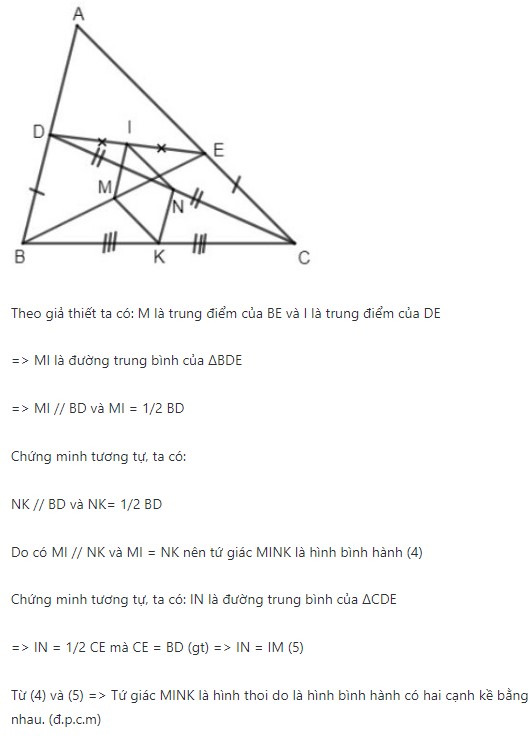
V. CHỨNG MINH TỨ GIÁC LÀ HÌNH CHỮ NHẬT
Cách 1: Chứng minh hình thang cân có một góc vuông là hình chữ nhật.
Ví dụ: Cho hình thang cân ABCD với cạnh AB song song với cạnh DC, giả sử góc D có số đo bằng 90 độ. Hãy chứng minh rằng tứ giác ABCD là một hình chữ nhật.
Hướng dẫn giải bài:

Cách 2: Chứng minh tứ giác có ba góc vuông là hình chữ nhật.
Ví dụ: Cho tứ giác ABCD có tam giác ABC vuông tại đỉnh A, tam giác BCD vuông tại đỉnh B, tam giác CDA vuông tại đỉnh C. Tứ giác ABCD là hình gì và tại sao?
Hướng dẫn giải bài:
Theo bài ra, ta có:
∆ABC vuông tại A ⇒ Góc CAB = 90°
∆BCD vuông tại B ⇒ Góc CBD = 90°
∆CDA vuông tại C ⇒ Góc ACD = 90°
⇒ Góc ADC = 90° (Tổng bốn góc trong của một tứ giác bằng 360 độ)
⇒ Tứ giác ABCD là hình chữ nhật do có bốn góc vuông. (đ.p.c.m)
Cách 3: Chứng minh hình bình hành có hai đường chéo bằng với nhau là hình chữ nhật
Ví dụ: Cho tam giác ABC cân tại đỉnh A, các đường trung tuyến BM và đường CN giao nhau tại điểm G. Gọi D là điểm đối xứng với điểm B qua điểm M, gọi E là điểm đối xứng với điểm G qua điểm N. Tứ giác BEDC là hình gì và tại sao?
Hướng dẫn giải bài:
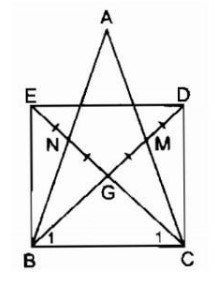

Cách 4: Chứng minh hình bình hành có một góc vuông là hình chữ nhật
Ví dụ: Cho tam giác ABC có góc ACB bằng 90 độ và độ dài cạnh AC bằng với cạnh BC. Trên cạnh AC và cạnh BC lấy lần lượt các điểm P và điểm Q sao cho độ dài AP bằng với CQ. Từ điểm P vẽ PM song song với BC (điểm M nằm trên cạnh AB). Hãy chứng minh tứ giác PCQM là một hình chữ nhật.

VI. CHỨNG MINH TỨ GIÁC LÀ HÌNH VUÔNG
Cách 1: Chứng minh tứ giác là hình thoi có một góc vuông
Ví dụ: Cho hình vuông ABCD. Trên bốn cạnh AB, BC, CD, DA lấy lần lượt theo thứ tự các điểm E, K, Q, P sao cho độ dài của bốn đoạn AE, BK, DQ, CP bằng với nhau. Tứ giác EKPQ là hình gì và tại sao?
Hướng dẫn giải bài:
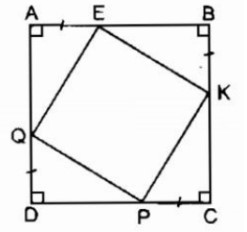

Cách 2: Chứng minh tứ giác là hình chữ nhật có hai cạnh kề bằng với nhau
Ví dụ: Cho tam giác ABC có độ dài cạnh AB bằng với cạnh AC, góc BAC bằng 90 độ. Trên cạnh BC lấy các điểm H và G sao cho độ dài ba đoạn BH, HG, GC bằng với nhau. Qua H và G kẻ các đường vuông góc với BC chúng cắt AB, AC theo thứ tự ở E và F. HÃy cho biết tứ giác EFGH là hình gì và tại sao?
Hướng dẫn giải bài:

Cách 3: Chứng minh tứ giác là hình chữ nhật có đường chéo là đường phân giác của một góc
Ví dụ: Cho tam giác ABC vuông tại đỉnh A. Đường phân giác AD. Gọi điểm M và điểm N lần lượt là chân đường vuông góc kẻ từ điểm D đến đoạn AB và đoạn AC. Chứng minh rằng tứ giác AMDN là một hình vuông.
Hướng dẫn giải bài:

Bài viết tổng hợp dạng bài về tứ giác trên đây thật là dễ hiểu phải không các em? Những kiến thức bên trên đều được HOCMAI chắt lọc và tổng hợp từ sách giáo khoa của các em vậy nên các em hoàn toàn có thể yên tâm đó chính là những kiến thức chính thống và có thể áp dụng vào bài làm của mình trong những kì thi và buổi kiểm tra. HOCMAI mong rằng các em sẽ học tập thật chăm chỉ để không phụ lòng bố mẹ và thầy cô nhé. Các em hãy truy cập website hoctot.hocmai.vn để tìm thêm thật nhiều bài học bổ ích nữa nhé!
















