“Tiếp tuyến của đường tròn” là một trong những đơn vị kiến thức về hình học quan trọng, cũng như thường xuyên xuất hiện trong đề thi môn Toán vào 10. Cùng theo dõi hướng dẫn của thầy Nguyễn Mạnh Cường về chủ đề này trong chương trình livestream “Trang bị kiến thức vào 10 cùng HOCMAI” nhé!
Những khái niệm về tiếp tuyến của đường tròn

Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP
- Định nghĩa: Đường thẳng d được gọi là tiếp tuyến của một đường tròn khi và chỉ khi đường thẳng đó một điểm chung duy nhất với đường tròn.
d tiếp xúc với (O;R) tại điểm M khi M là điểm chung duy nhất của d và (O).
2. Dấu hiệu nhận biết:
- d⊥OM tại điểm M (M ∈ (O))
- Khoảng cách từ tâm O đến đường thẳng d bằng độ dài bán kính R.
3. Định lí về giao hai tiếp tuyến: Nếu MA và MB là hai tiếp tuyến của (O) lần lượt tại A, B. Khi đó:
- Điểm M cách đều hai tiếp điểm, tức MA = MB.
- MO là phân giác AMB.
Một số bài tập vận dụng kiến thức
Bài 1: Cho góc xOy= 60°, có tia phân giác là Oz. Lấy M ∈ Oz, OM = 12cm. Chứng minh rằng: Ox là tiếp tuyến của đường tròn (M; 6cm).

Lời giải:
Kẻ MH⊥Oy tại H.
Vì Oz là phân giác của ^xOy nên ^MOH = 1/2^xOy = 30°
Xét góc MOH vuông tại H ta có:
sin^MOH= MH/OM ⇒ MH = OM.sin30° = 12 x 1/2 = 6 (cm) = R
Do đó: d[M;Ox] = MH = 6cm = R
⇒ Ox là tiếp tuyến của (M; 6cm)
Bài 2: Cho hình vuông ABCD. M, N lần lượt là trung điểm của BC, CD. AM và BN giao nhau tại điểm I. Chứng minh rằng: BN tiếp xúc với đường tròn (A; AI).

Lời giải:
Xét ΔAMB và ΔBCN có:
AB = BC
^ABM=^BCN=90°
BM = 1/2 BC = 1/2 CD = CN
ΔAMB = ΔBCN (c.g.c) ^MAB= ^NBC
Xét ΔABI có: ^IAB + ^IBA = ^ABI + ^IBM=90° ⇒ BN⊥AI tại I hay BN là tiếp tuyến của (A; AI).
Bài 3: ΔABC vuông tại A, có đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB và AC. Chứng minh rằng: DE là tiếp tuyến của đường tròn ngoại tiếp ΔBDH.

Lời giải:
Gọi O là trung điểm của BH
Vì ΔBDH vuông tại D nên DO = 1/2 BH = BO = OH ⇒ O là tâm đường tròn ngoại tiếp ΔBDH
ΔAHC vuông tại H có ^HAE + ^C= 90°
ΔABC vuông tại A có ^OBD + ^C= 90°
^HAE = ^OBD(1)
Mặt khác: ADHE là hình chữ nhật ^HAE = ^HDE(2)
ΔOBD cân tại O nên ^OBD=^BOD (3)
Từ (1), (2) và (3)^HDE=^BDO ⇒ ^HDE+ ^ODH= ^BDO+ ^ODH
hay ^ODE= ^BDH, mà ^BDH=90° ⇒ ^ODE= 90°
⇒DE⊥OD tại D ⇒ DE là tiếp tuyến của đường tròn ngoại tiếp ΔBDH
Bài 4: (Trích đề thi vào 10 môn Toán của tỉnh An Giang năm học 2017 – 2018)
Ngọn hải Đăng Kê Gà ở tỉnh Bình Thuận là ngọn tháp thắp đèn gần bờ biển dùng để định hướng cho tàu thuyền giao thông trong khu vực vào ban đêm. Đây là ngọn hải đăng được xem là cổ xưa và cao nhất Việt Nam, chiều cao của ngọn đèn so với mặt nước biển là 65m. Hỏi:
a) Một người quan sát đứng tại vị trí đèn của Hải đăng thì nhìn được tối đa bao nhiêu km trên mặt biển?
b) Cách bao xa thì một người quan sát đứng ở trên tàu bắt đầu trông thấy ngọn đèn này, biết rằng mắt người quan sát đứng ở trên tàu có độ cao 5m so với mặt nước biển?
(Cho biết bán kính Trái Đất gần bằng 6400km và điều kiện quan sát trên biển là không bị che khuất).
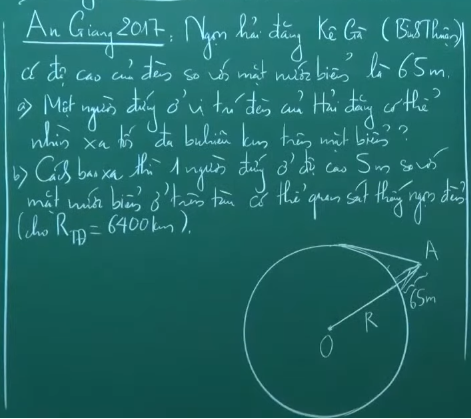
Để nắm được hướng dẫn giải chi tiết của bài toán thực tế này, các bạn học sinh tìm hiểu ngay trong video dưới đây:
Livestream “Trang bị kiến thức vào 10 cùng HOCMAI” – Môn Toán: Tiếp tuyến của đường tròn – Thầy Nguyễn Mạnh Cường
>>> Ngoài ra, học sinh có thể xem trọn bộ bài giảng luyện thi vào 10 môn Toán(đầy đủ các chuyên đề trọng tâm) của thầy Cường TẠI ĐÂY
Hy vọng với những chia sẻ của thầy Cường về nội dung “Tiếp tuyến của đường tròn” cũng như phân tích các ví dụ về chứng minh tiếp tuyến sẽ giúp các bạn hiểu hơn về phần kiến thức này. Để xem thêm bài giảng luyện thi vào 10 đầy đủ các môn, các bạn có thể tham khảo Chương trình HM10 Toàn diện với hệ thống bài giảng chất lượng và lộ trình bài bản từ Trang bị kiến thức – Tổng ôn – Luyện đề giúp học sinh lớp 9 chinh phục hiệu quả những kiến thức của môn thi vào 10.
>> ĐĂNG KÝ HỌC THỬ MIỄN PHÍ BÀI GIẢNG ĐẦY ĐỦ CÁC MÔN THI VÀO 10<<
ĐĂNG KÝ GIẢI PHÁP HM10 TOÀN DIỆN 2021 – 2022
|


















![[HOCMAI] Chào năm mới 2024: ĐÓN TẾT RỒNG VÀNG – NHẬN QUÀ HOÀNH TRÁNG!](https://hoctot.hocmai.vn/wp-content/uploads/2024/01/1920x1080-100x70.png)


