Phương trình quy về phương trình bậc hai

Phương trình quy về phương trình bậc hai là dạng bài tập luyện thi không thể thiếu dành cho các bạn học sinh THPT, đặc biệt trong quá trình học Toán lớp 9 và đang ôn thi vào lớp 10. Bài viết này HOCMAI tóm tắt toàn bộ kiến thức lý thuyết, các dạng toán và ví dụ cụ thể về từng dạng của phương trình bậc hai quy về một ẩn.

 

I. Tóm tắt lý thuyết quan trọng cần nhớ về phương trình quy về phương trình bậc hai

1. Phương trình trùng phương

a) Phương trình trùng phương là kiểu phương trình có dạng:

b) Cách giải phương trình trùng phương: 

Đưa phương trình về phương trình bậc hai bằng cách đặt ẩn phụ t = x^2 (t 0) để: 

2. Phương trình chứa ẩn ở mẫu thức

a) Phương trình chứa ẩn ở mẫu là phương trình có biểu thức chứa ẩn ở dưới mẫu.

Ví dụ:

b) Cách giải phương trình chứa ẩn ở mẫu thức: 

Để giải phương trình chứa ẩn ở mẫu, ta sẽ giải theo các bước như sau:

• Bước 1: Tìm ĐKXĐ (Điều kiện xác định) của ẩn tại phương trình.
• Bước 2: Khử mẫu bằng cách quy đồng mẫu thức hai vế.
• Bước 3: Giải phương trình vừa sau bước 2.
• Bước 4: So sánh các nghiệm vừa tìm được tại bước 3 với ĐKXĐ và đưa ra kết luận.

Vì chứa ẩn ở dưới mẫu (đại lượng chưa biết) nên chưa thể khẳng định mẫu thức khác 0. Đây là điều kiện bắt buộc để một phân thức tồn tại (hay có nghĩa). Vì vậy việc tìm điều kiện xác định rất quan trọng trong việc tìm nghiệm của một phương trình => Giúp loại bỏ các g.trị của ẩn làm cho mẫu thức bằng 0.

3. Phương trình đưa về dạng tích

1. a) Tìm hiểu về phương trình tích: 

Phương trình (ẩn x) là phương trình có dang: A(x) B(x) = 0, trong đó A(x) và B(x) là các đa thức ẩn x.

Ví dụ:

b) Cách giải phương trình đưa về dạng tích: 

• Bước 1: Phân tích vế trái trở thành nhân tử, vế phải bằng 0.
• Bước 2: Xét từng nhân tử ở bước 1 bằng 0 để tìm nghiệm.

Ví dụ 1: Giải phương trình: A(x) B(x) = 0

4. Một số dạng phương trình quy về phương trình bậc 2 khác thường gặp

Ngoài 4 dạng đã giới thiệu ở trên, sau đây là một số dạng phương trình có thể quy về phương trình bậc hai thường gặp do HOCMAI tổng hợp gửi đến bạn:

a. Phương trình bậc bốn dạng:

b. Phương trình bậc bốn dạng:

c. Phương trình đối xứng bậc bốn có dạng:

d. Phương trình hồi quy có dạng:

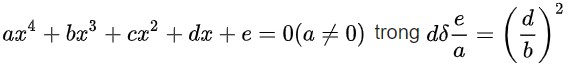
e. Phương trình phân thức hữu tỉ:
Khi làm bài tập về phương trình phân thức hữu tỉ, chúng ta sẽ cần phân tích một số dạng sau:

 

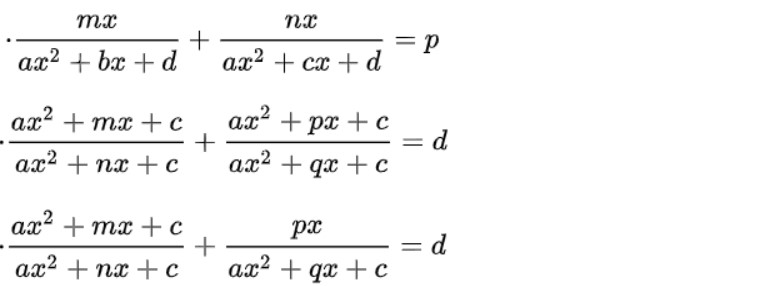
II. Các dạng toán phương trình quy về phương trình bậc hai thường gặp

Dạng 1 – Giải phương trình trùng phương

Xem lại phần lý thuyết và cách giải dạng toán Giải phương trình trùng phương ở phần I.

Ví dụ: Tìm các nghiệm của phương trình: x^4 – 6x^2 + 8 = 0

Lời giải

Dạng 2 – Giải phương trình chứa ẩn ở mẫu thức

Xem lại phần lý thuyết và cách giải dạng toán Giải phương trình chứa ẩn ở mẫu thức ở phần I.

Ví dụ: Tìm tập nghiệm của phương trình cho trước:

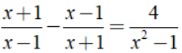
Lời giải

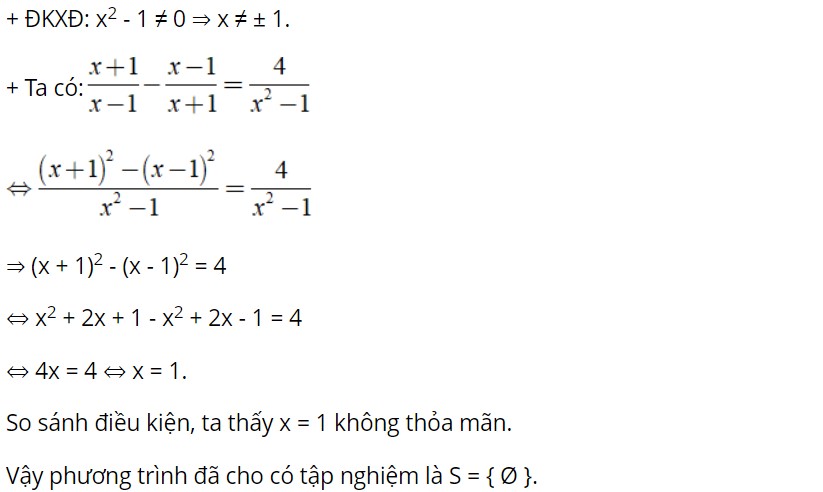
Dạng 3 – Phương trình đưa về dạng phương trình tích

Xem lại phần lý thuyết và cách giải dạng toán Phương trình đưa về dạng phương trình tích ở phần I.

Ví dụ: Giải phương trình: (x + 3) x (x – 2) = 0

Lời giải

Dạng 4 – Giải phương trình bằng cách đặt ẩn phụ

Giải hệ phương trình bằng cách đặt ẩn phụ là dạng toán nâng cao hơn của dạng hệ phương trình bậc nhất với phương pháp cộng và phương pháp thế.

Khi giải dạng toán này, chúng ta cần đặt và tìm điều kiện của ẩn phụ trước, tiếp đó mới vận dụng phương pháp cộng đại số hoặc phương pháp thế để giải hệ. Cách làm chi tiết gồm 4 bước: 

• Bước 1: Đặt điều kiện để hệ phương trình đề ra có nghĩa.
• Bước 2: Đặt và tìm điều kiện của ẩn phụ
• Bước 3: Tiến hành giải hệ phương trình theo ẩn phụ đã đặt bằng phương pháp cộng đại số hoặc phương pháp thay thế.
• Bước 4: Quay lại ẩn ban đầu để tìm nghiệm của hệ phương trình. 

Ví dụ: Giải phương trình sau:

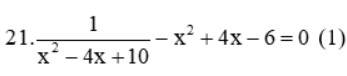
Lời giải

Dạng 5 – Giải phương trình chứa căn thức bậc 2

a) Tìm hiểu về phương trình tích chứa căn thức bậc 2:

Phương trình chứa căn bậc 2 là phương trình chứa đại lượng √f(x).

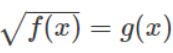
b) Cách giải phương trình đưa về dạng tích: 

Để giải dạng toán này, chúng ta luôn phải tìm điều kiện để biểu thức trong căn có nghĩa trước khi giải, tức là tìm khoảng giá trị của x để f(x) ≥ 0.

Có 3 bước để giải dạng toán này:

• Bước 1: Tìm ĐK của x để f(x) ≥ 0; g(x) ≥ 0.
• Bước 2: Bình phương hai vế rồi tiến hành rút gọn.
• Bước 3: Giải phương trình để tìm x, kiểm tra xem có thỏa mãn với ĐK hay không => Kết luận.

Ví dụ:

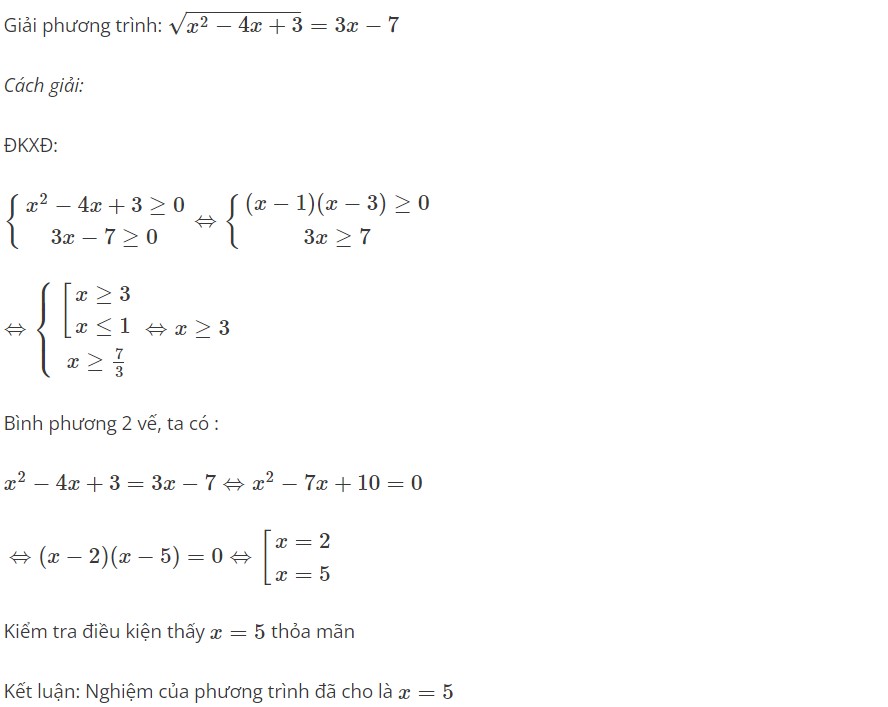
Dạng 6 – Xác định số giao điểm giữa đường thẳng và Parabol

Sự tương giao giữa:

• Parabol (P): y = ax^2 (a 0) 
• Đường thẳng d: y = mx + n

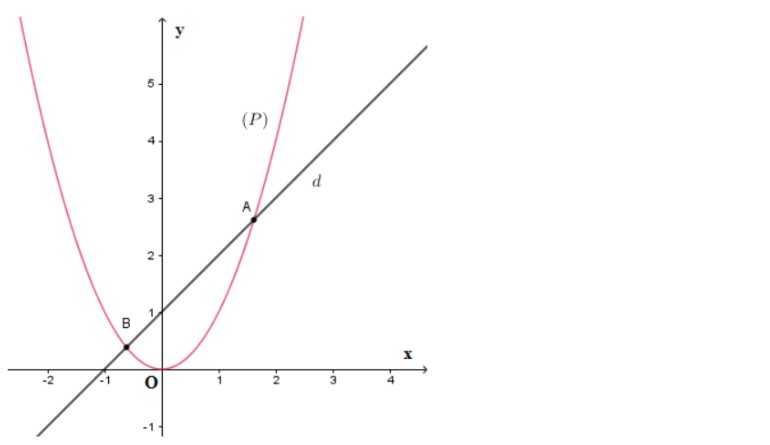
Số giao điểm của đường thẳng d và parabol (P) là số nghiệm của phương trình hoành độ giao điểm:

Sẽ xảy ra 3 trường hợp:

• Δ > 0 => Phương trình có 2 nghiệm phân biệt => Đường thẳng d cắt Parabol (P) tại 2 điểm phân biệt.
• Δ = 0 => Phương trình có nghiệm kép => Đường thẳng d tiếp xúc với Parabol (P).
• Δ = 0 => Phương trình vô nghiệm => Đường thẳng d không cắt Parabol (P).

Dạng 7 – Tìm tọa độ giao điểm của đường thẳng và Parabol

Để tìm giao điểm của đường thẳng d = y = mx + n và Parabol (P) y = ax^2 (a 0), ta sẽ làm theo các bước:

• Bước 1: Xét phương trình hoành độ giao điểm: ax^2 = mx + n (a 0).
• Bước 2: Tiến hành giải phương trình vừa tìm được => Tìm được x và y => Tọa độ (x;y).

Ví dụ: Tìm tọa độ giao điểm của: đường thẳng y = 2x – 1 và Parabol y = x^2

Lời giải

Dạng 8 – Xác định tham số m để đường thẳng và Parabol thỏa mãn điều kiện cho trước

Cách xác định m để đường thẳng d = y = mx + n và Parabol (P) y = ax^2 (a 0) cắt nhau tại điểm thỏa mãn cho trước. Ta sẽ làm theo các trường hợp sau:

Ví dụ: Cho đường thẳng (d): y = (m + 1)x + 3 và Parabol (P): y = mx^2, với m là tham số (m ≠ 0, m ≠ -1). Tọa độ giao điểm của (d) và (P) khi m = 1.

Lời giải

Dạng 9 – Tính diện tích tam giác, diện tích hình thang và chiều cao

Để giải dạng bài tập này, bạn cần vận dụng linh hoạt các công thức tính diện tích tam giác, hình thang để làm bài.

 

Các bài viết liên quan:

• Hệ thức Viet

• Giải hệ phương trình bằng phương pháp cộng đại số

 

 

Bài viết này HOCMAI đã giúp các bạn học sinh tóm tắt lý thuyết quan trọng cần nhớ về phương trình quy về phương trình bậc hai và các dạng bài cơ bản. Hy vọng những kiến thức bổ ích trên sẽ giúp các bạn học sinh trong quá trình làm bài tập Toán lớp 9 cũng như trong quá trình ôn thi vào 10 môn Toán.