Xin chào các em học sinh khối 8, nếu các em đang loay hoay với đang loay hoay ôn thi, không biết mình nên ôn tập lại kiến thức từ đâu? kiến thức nào là trọng tâm? tìm bài tập để ôn luyện ở đâu để vượt qua kỳ thi giữa kì 1 môn toán? thì bài viết này là dành cho các em đó. Bài viết đề cương ôn thi giữa kì 1 toán 8 dưới đây sẽ đưa cho các em đầy đủ kiến thức hình học, đại số và bài tập để các em luyện tập. Hãy cùng vào bài thôi nào!
A. KIẾN THỨC TRỌNG TÂM
I. ĐẠI SỐ – CHƯƠNG I TOÁN 8: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
1. Nhân đơn thức với đa thức:
Để nhân một đơn thức với một đa thức thì ta nhân đơn thức với từng số hạng của đa thức rồi sau đó cộng các tích với nhau.
Ví dụ: Cho A, B, C, D là các đơn thức, ta có: A(B + C – D) = AB + AC – AD
2. Nhân đa thức với đa thức:
Để nhân một đa thức với một đa thức thì ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi sau đó cộng các tích với nhau.
Ví dụ: Cho A, B, C, D là các đa thức ta có:
(A + B)(C + D)
= A(C + D) + B(C + D)
= AC + AD + BC + BD
3. Những hằng đẳng thức đáng nhớ:
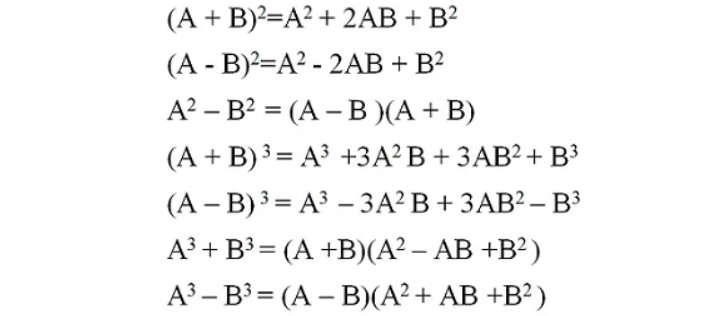
4. Phân tích đa thức trở thành những nhân tử
– Phương pháp → đặt nhân tử chung
– Phương pháp → dùng hằng đẳng thức
– Phương pháp → nhóm hạng tử
– Phương pháp → phối hợp nhiều phương pháp
5. Chia đơn thức cho đơn thức
Quy tắc: Để chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) thì ta làm như sau:
– Lấy hệ số của đơn thức A chia cho hệ số của đơn thức B.
– Lấy lũy thừa của từng biến trong A chia cho lũy thừa của cùng biến đó trong B.
– Nhân những kết quả vừa tìm được lại với nhau.
6. Chia đa thức cho đơn thức
Quy tắc: Nếu chia đa thức A cho đơn thức B (trong trường hợp các hạng tử của đa thức A đều chia hết cho đơn thức B) thì ta chia mỗi hạng tử của A cho B rồi cộng các kết quả đó với nhau.
7. Chia đa thức một biến đã được sắp xếp
Quy tắc: Ta sẽ trình bày phép chia tương tự với cách chia các số tự nhiên. Với hai đa thức một biến là A và B, B ≠ 0, chỉ tồn tại duy nhất hai đa thức Q và R sao cho:
A = B.Q + R với R = 0 hoặc R ≠ 0, có bậc bé hơn bậc của B.
– Nếu R = 0 → ta được phép chia hết.
– Nếu R ≠ 0 → ta được phép chia có dư.
II. HÌNH HỌC – CHƯƠNG I TOÁN 8: TỨ GIÁC
1. Định nghĩa, tính chất và dấu hiệu nhận biết của những hình tứ giác
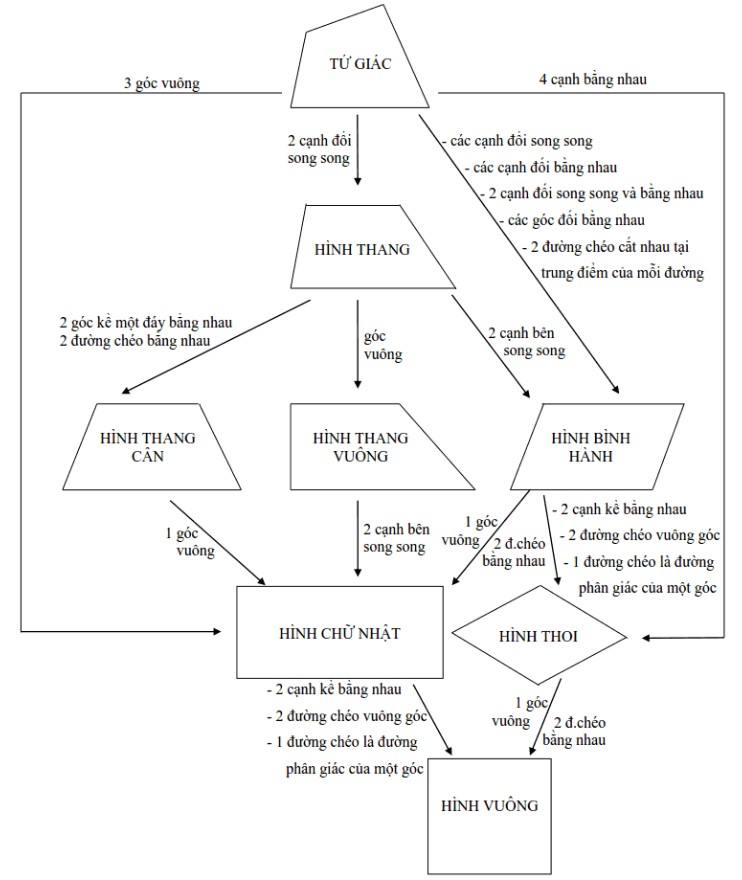
Sơ đồ nhận biết các loại tứ giác
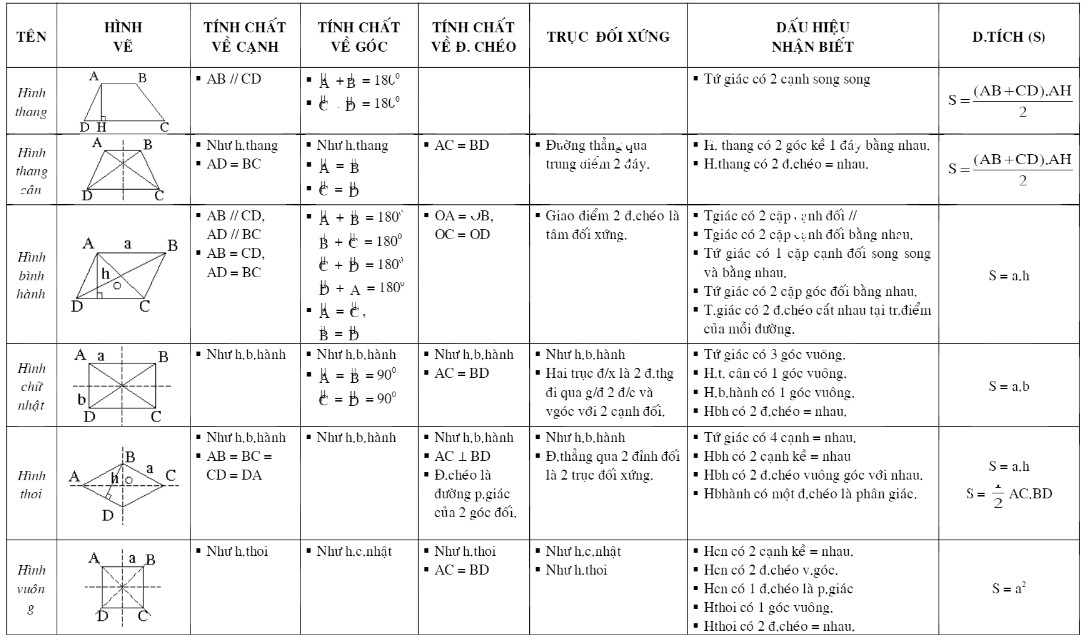
Định nghĩa, tính chất và dấu hiệu nhận biết của những hình tứ giác
2. Đường trung bình của tam giác và hình thang

B. BÀI TẬP ÔN THI GIỮA KÌ I TOÁN 8 (Đại số và Hình học)
I. ĐẠI SỐ
Bài 1: Thực hiện phép nhân:
a. (3x + 5)(2x – 7)
b. (-5x + 2)(-3x – 4)
c. (x – 5)(-x² + x +1)
d. (x² – 2x – 1)(x – 3)
Hướng dẫn giải bài:
a. (3x + 5)(2x – 7)
= 3x.2x + 5.2x + 3x.(-7) + 5.(-7)
= 6x² + 10x – 21x – 35
= 6x² – 11x – 35
b. (-5x + 2)(-3x – 4)
= -5x.(-3x) + 2(-3x) + (-5x)(-4) + 2. (-4)
= 15x² – 6x + 20x – 8
= 15x² + 14x – 8
c. (x – 5)(-x² + x + 1)
= -x³ + x² + x + 5x² – 5x – 5
= -x³ +(x² + 5x²) + (x – 5x) – 5
= -x³ +6x² – 4x – 5
d. (x² – 2x – 1)(x – 3)
= x².x – 2x.x -1.x +x².(-3) – 2x.(-3) – 1.(-3)
= x³ – 2x² – x – 3x² + 6x + 3
= x³ – (2x² + 3x²) + (-x + 6x) + 3
= x³ – 5x² + 5x + 3
Bài 2: Tính giá trị biểu thức:
a. 6x(2x – 7) – (3x – 5)(4x + 7) với x = -2
b. x³ – 9x² + 27x – 27 với x = 5
c. x³ + y³ – 3x² + 3xy – 3y² biết rằng x + y = 3
Hướng dẫn giải bài:
a. 6x(2x – 7) – (3x – 5)(4x + 7) với x = -2
6x(2x – 7) – (3x – 5)(4x + 7)
= 12x² – 42x -3x(4x + 7) + 5(4x + 7)
= 12x² – 42x – 12x² – 21x + 20x + 35
= (12x² – 12x²) + (-42x – 21x + 20x)+ 35
= – 43x + 35
Thay x = -2 vào biểu thức trên, ta có: -2.(-43) + 35 = 121
b. x³ – 9x² + 27x – 27 tại x = 5
x³ – 9x² + 27x – 27
= (x – 3)³
Thay x = 5 vào biểu thức trên, ta có: (5 – 3)³ = 2³ = 8
c. x³ + y³ – 3x² + 3xy – 3y² biết x + y = 3
x³ + y³ – 3x² + 3xy – 3y²
= x³ + y³ – 3(x² + xy – y²)
Với x + y = 3 ta có:
x³ + y³ – 3(x² + xy – y²)
= x³ + y³ – (x + y)(x² + xy – y²)
= x³ + y³ – (x³ + y³) = 0
Bài 3: Hãy chứng minh rằng giá trị của những biểu thức sau không phụ thuộc vào giá trị của biến:
a. 5x² – (2x + 1)(x – 2) – x(3x + 3) + 7
b. (3x – 1)(2x + 3) – (x – 5)(6x – 1) – 38x
c. (5x – 2)(x + 1) – (x – 3)(5x – 1) – 17(x – 2)
Hướng dẫn giải bài:
a. 5x² – (2x + 1)(x – 2) – x(3x + 3) + 7
= 5x² – 2x² + 4x – x + 2 – 3x² – 3x + 7
= ( 5x² – 2x² – 3x²) + (4x – x – 3x) + 2 + 7
= 9
Vậy: giá trị của biểu thức trên → không phụ thuộc vào giá trị của biến.
b. (3x – 1)(2x + 3) – (x – 5)(6x – 1) – 38x
= 6x² + 9x – 2x – 3 – 6x² + x + 30x + 5 – 38x
= 6x² + 7x – 3 – 6x² + 31x – 5 – 38x
= (6x² – 6x²) + (7x + 31x – 38x) – 3 – 5
= -8
Vậy: giá trị của biểu thức trên → không phụ thuộc vào giá trị của biến.
c. (5x – 2)(x + 1) – (x – 3)(5x – 1) – 17(x – 2)
= 5x² + 5x – 2x – 2 – (5x² + x – 15x – 3) – (17x – 34)
= 5x² + 3x – 2 – 5x² + 14x + 3 – 17x + 34
= (5x² – 5x²) + (3x + 14x – 17x) + (-2 + 3 + 34)
= 35
Vậy: giá trị của biểu thức trên → không phụ thuộc vào giá trị của biến.
Bài 4: Chứng minh rằng: các biểu thức sau không âm với mọi giá trị x:
a. x² – 8x + 20
b. x² – x + 1
c. 4x² – 12x + 11
Hướng dẫn giải bài:
a. x² – 8x + 20
= x² – 8x + 16 + 4
= (x – 8)² + 4
Vì (x – 8)² > 0 hoặc (x – 8)² = 0 với mọi x, nên (x – 8)² + 4 > 0
b. x² – x + 1
= x² – 2.(1/2).x + 1/4 + 3/4
= (x – 1/2)² + 3/4
Vì (x – 1/2)² > 0 hoặc (x – 1/2)² = 0 với mọi x, nên (x – 1/2)² + 3/4 > 0
c. 4x² – 12x + 11
= (2x)² – 2.2x.3 + 9 + 2
= (2x – 3)² + 2
Vì (2x – 3)² > 0 hoặc (2x – 3)² = 0 với mọi x, nên (2x – 3)² + 2 > 0
Bài 5: Phân tích những đa thức dưới đây thành nhân tử:
a. 5x² – 5xy -10x – 10y
b. a²x² – a²y² – b²x² + b²y²
c. x³ + 3x² – 16x – 48
Hướng dẫn giải bài:
a. 5x² – 5xy -10x – 10y
= 5x(x – y) – 10(x – y)
=5(x – 2)(x – y)
b. a²x² – a²y² – b²x² + b²y²
= (a² – b²)(x² – y²)
= (a – b)(a + b)(x – y)(x + y)
c. x³ + 3x² – 16x – 48
= x²(x + 3) – 16(x + 3)
= (x² – 16)(x + 3)
II. HÌNH HỌC
Bài 1: Cho ΔABC cân tại A. AM là đường cao. Gọi N là trung điểm của AC. D là điểm đối xứng của M qua N.
a) Hãy chứng minh rằng: Tứ giác ADCM là hình chữ nhật.
b) Hãy chứng minh rằng: Tứ giác ADMB là hình bình hành và BD đi qua trung điểm O của AM.
c) BD cắt AC tại I. Hãy chứng minh rằng DI = 2/3.OB
Hướng dẫn giải bài:
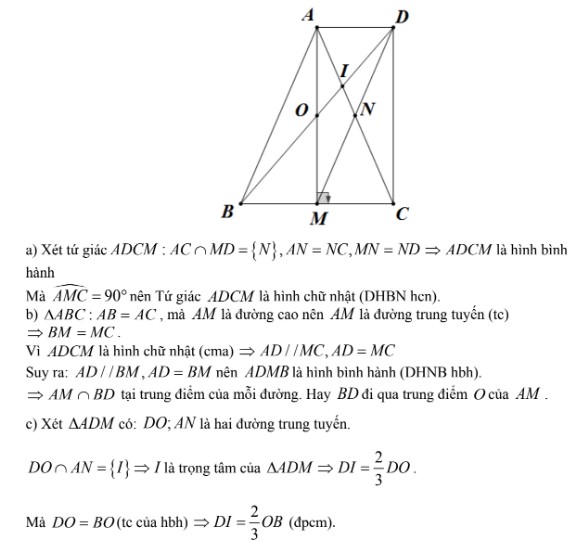
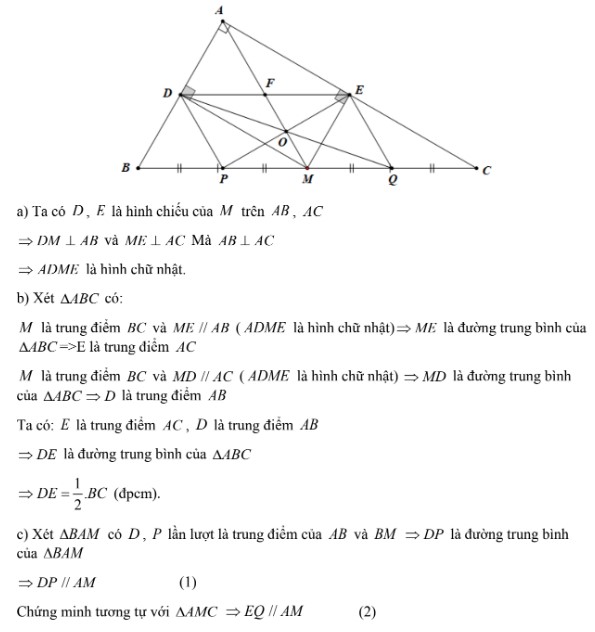
Bài 2: Cho ΔABC vuông tại A. M là trung điểm của BC. Gọi D và E lần lượt là hình chiếu của M trên đoạn AB và đoạn AC .
a) Tứ giác ADME là hình gì? Tại sao ?
b) Chứng minh rằng: DE = 1/2.BC
c) Lấy điểm Q là trung điểm của MC, điểm P là trung điểm của BM . Hãy chứng minh rằng tứ giác DPQE là hình bình hành. Từ đó chứng minh: tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM .
d) Tam giác ABC vuông ban đầu cần thêm điều kiện gì để hình bình hành DPQE là hình chữ nhật?
Hướng dẫn giải bài:

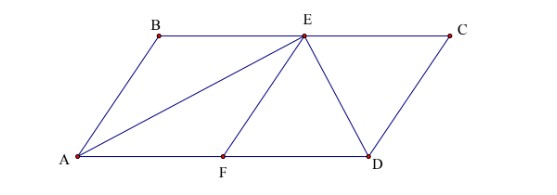
Bài 3: Cho hình bình hành ABCD có BC = 2AB và góc A bằng 60 độ .Gọi E và F theo thứ tự là trung điểm của đoạn BC và đoạn AD .
a, Tứ giác ECDF là hình gì?
b, Tứ giác ABED là hình gì? Vì sao?
c, Tính số đo góc AED.
Hướng dẫn giải bài:

Các em có thể tham khảo kiến thức liên quan tại bài viết:
Trên đây là bài viết đề cương ôn thi giữa kì 1 toán 8.Bài viết này HOCMAI đã tổng hợp rất đầy đủ kiến thức và bài tập để các em có thể an tâm đi thi. Chỉ cần các em học thuộc lòng lý thuyết và làm thêm nhiều bài hơn nữa thì bài thi giữa kì 1 sẽ trở nên thật dễ dàng. Nếu như có bất kỳ khó khăn hay thắc mắc nào trong quá trình luyện thi, các em hãy chủ động hỏi thầy cô và bạn bè nhé. Để tìm thêm những đề cương của đa dạng các môn, các em học sinh hãy truy cập hoctot.hocmai nhé!




















