Đề cương ôn thi học kì 2 toán 8 mới nhất

Bài viết dưới đây là bài Đề cương ôn thi học kì 2 toán 8 mới nhất dành cho các em học sinh khối 8. Kỳ thi cuối kỳ này sẽ tổng hợp kiến thức của toàn kỳ 2 nên các em cần khắt khe, chăm chỉ ôn luyện đấy. HOCMAI gửi em bài viết này để hỗ trợ các em ôn tập, bài viết này được biên soạn rất chi tiết và đầy đủ kiến thức lý thuyết, bài tập, dạng đề sát sườn với sách giáo khoa trên trường của các em. Chúng ta cùng vào bài thôi nhé!

A. LÝ THUYẾT – ĐỀ CƯƠNG ÔN TẬP TOÁN 8 HỌC KÌ 2

I. Ôn tập toán đại 8 học kì 2

Chương III Đại số 8 → Phương trình bậc nhất một ẩn

1) Phương trình bậc nhất một ẩn

Dạng: ax + b = 0 (với a, b là các số cho trước và với a ≠ 0)

2) Hai quy tắc để biến đổi phương trình

– Quy tắc chuyển vế:

Nếu a = b ⇒ a + c = b + c

Nếu a + c = b + c ⇒ a = b

Nếu a = b ⇒ b = a

Khi một số hạng tử từ vế này được chuyển sang vế bên kia trong một đẳng thức thì ta cần phải đổi dấu của số hạng ấy: dấu “+” trở thành dấu “-” và ngược lại dấu “-” trở thành dấu “+”.

– Quy tắc nhân với một số

3) Phương trình tích

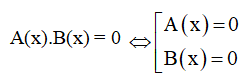
4) Cách để giải phương trình chứa ẩn ở dưới mẫu số.

Bước 1 → Tìm ra điều kiện xác định của phương trình.

Bước 2 → Quy đồng mẫu số ở hai vế của phương trình rồi sau đó khử mẫu.

Bước 3 → Giải phương trình vừa nhận được ở bước 2 trên.

Bước 4 → Đưa ra kết luận. Trong những giá trị ẩn vừa tìm được ở trên bước 3, những giá trị mà thỏa mãn được ĐKXĐ thì chính là nghiệm của phương trình này.

5) Giải bài toán bằng phương pháp lập phương trình.

Bước 1 → Lập phương trình.

– Chọn ra ẩn số và đặt ra điều kiện thích hợp cho ẩn số đó.

– Biểu diễn những đại lượng chưa biết theo ẩn và những đại lượng đã biết.

– Lập phương trình biểu thị ra mối quan hệ giữa những đại lượng ấy.

Bước 2 → Giải phương trình.

Bước 3 → Trả lời: Kiểm tra xem trong những nghiệm của phương trình ấy, nghiệm nào thì thỏa mãn được điều kiện của ẩn, nghiệm nào không thỏa mãn, rồi đưa ra kết luận.

Chương IV Đại số 8 → Bất phương trình bậc nhất một ẩn

1) Liên hệ giữa thứ tự và phép tính (Phép cộng và phép nhân)

Với ba số a, c và b bất kì, có:

+) Nếu có a ≤ b thì a + c ≤ b + c

+) Nếu có a < b thì a + c < b + c

+) Nếu có a ≤ b và c > 0 thì ac ≤ bc

+) Nếu có a < b và c > 0 thì ac < bc

+) Nếu có a ≤ b và c < 0 thì ac ≤ bc

+) Nếu có a < b và c < 0 thì ac > bc.

2) Bất phương trình bậc nhất một ẩn

Dạng: ax + b < 0 (hoặc ax + b > 0; ax + b ≤ 0; hoặc ax + b ≥ 0)

Trong đó a, b là những số đã cho và giá trị a ≠ 0.

3) Tập nghiệm và cách biểu diễn tập nghiệm của bất phương trình trên trục số

Bất phương trình – Tập nghiệm của bất phương trình – Biểu diễn tập nghiệm đó ở trên trục số

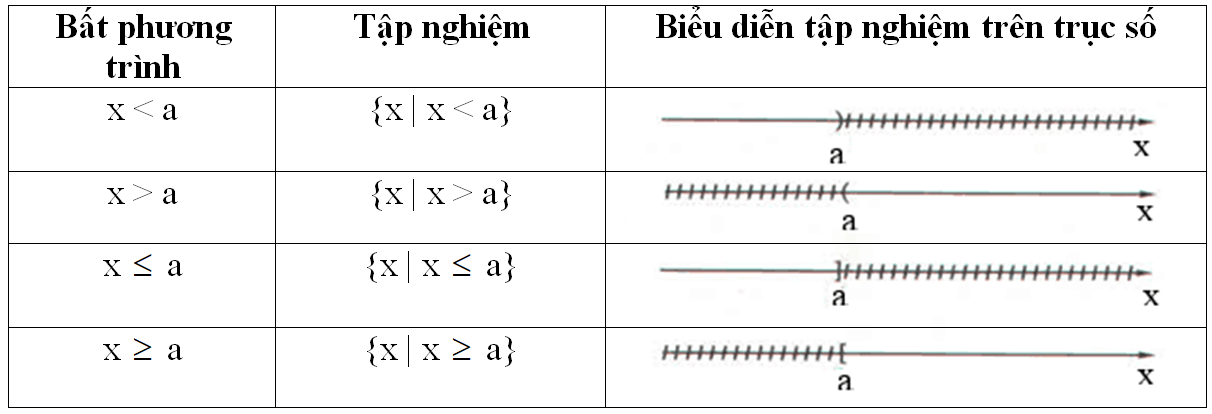
4) Quy tắc chuyển vế:

Khi chuyển vế của một hạng tử từ vế này sang vế bên kia của một bất phương trình thì cần phải đổi dấu của hạng tử đó.

5) Quy tắc nhân

Khi nhân cả hai vế của một bất phương trình với cùng một số có giá trị khác 0, ta phải:

– Giữ nguyên chiều của bất đẳng thức nếu số đó là số dương.

– Đổi chiều của bất đẳng thức nếu số đó là số âm.

6) Trong phương trình chứa dấu giá trị tuyệt đối

– Phải áp dụng định lý của giá trị tuyệt đối.

– Giải phương trình mà không chứa dấu giá trị tuyệt đối.

– Chọn ra nghiệm thích hợp ở trong trường hợp đang xét tới.

– Tính chất: 

II. Ôn tập toán hình 8 học kì 2

Chương III Hình học 8 → Tam giác đồng dạng

1) Đoạn thẳng tỉ lệ: Cặp đoạn thẳng CD và AB mà tỉ lệ với cặp đoạn thẳng C’D’ và A’B’ khi và chỉ khi:

2) Một vài tính chất của tỉ lệ thức:

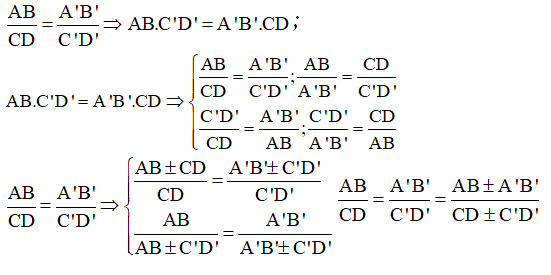
3) Định lí TaLet ở trong tam giác:

Nếu như một đường thẳng giao với hai cạnh của một tam giác và đồng thời song song với cạnh còn lại của tam giác thì nó sẽ định ra trên hai cạnh đó những đoạn thẳng tỷ lệ tương ứng.

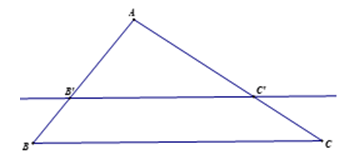
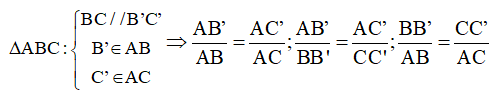
4) Định lí đảo của định lí TaLet:

Nếu có một đường thẳng giao với hai cạnh của một tam giác và định ra ở trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ thì ta có đường thẳng đó song song với cạnh còn lại của tam giác.

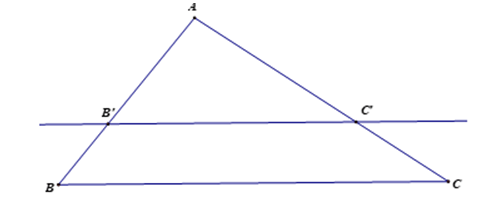
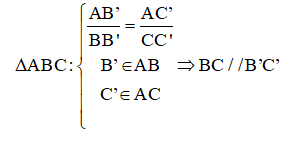
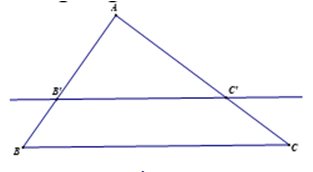
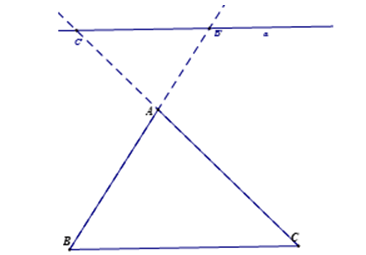
5) Hệ quả của định lí TaLet:

Nếu một đường thẳng giao với hai cạnh của một tam giác và song song với cạnh thứ ba thì nó sẽ tạo thành một tam giác mới và ba cạnh của tam giác và ba cạnh của tam giác đã cho tương ứng tỷ lệ với nhau.

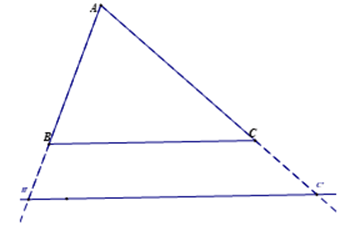
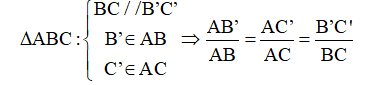
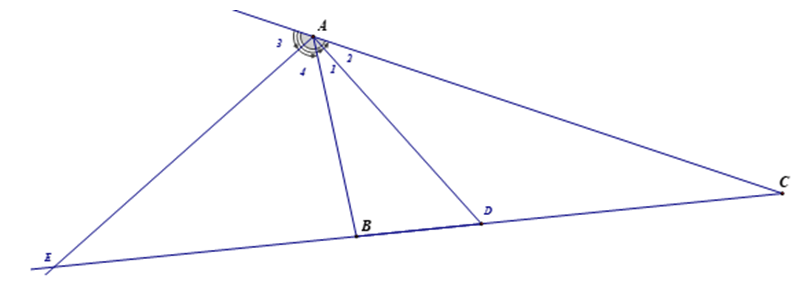
6) Tính chất đường phân giác trong tam giác:

Trong một tam giác, đường phân giác của một góc chia cạnh đối diện góc ấy thành hai đoạn thẳng có tỉ lệ tương ứng với 2 cạnh kề với hai đoạn ấy.

7) Hai tam giác đồng dạng:

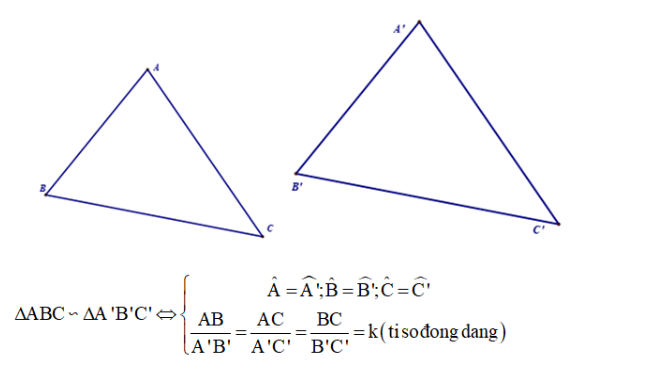
8) Tính chất của hai tam giác đồng dạng

Gọi p, p’, S, S’, h, h’ lần lượt là chu vi, diện tích và chiều cao của 2 tam giác đồng dạng với nhau là: ABC và A’B’C’.

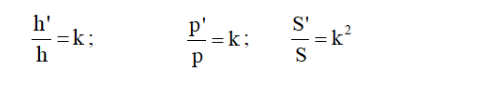
9) Những trường hợp đồng dạng của tam giác thường

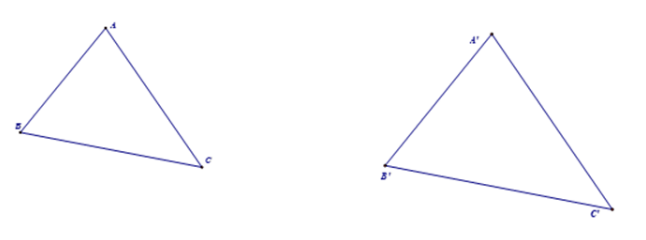
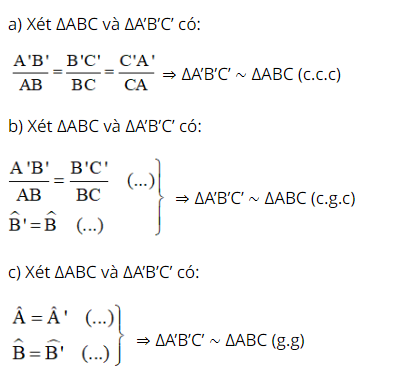
10) Những cách chứng minh đồng dạng của hai tam giác vuông:

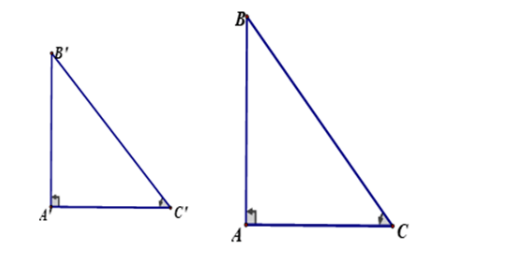
Trường hợp 1 → Nếu cho hai tam giác vuông có một góc nhọn bằng nhau thì hai tam giác đó đồng dạng.

Trường hợp 2 → Nếu có hai cạnh góc vuông của tam giác vuông này tỉ lệ tương ứng với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

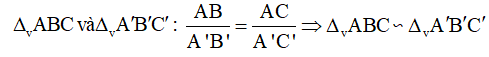
Trường hợp 3 → Nếu có cạnh huyền và cạnh góc vuông của tam giác vuông này tỉ lệ tương ứng với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng nhau.

Chương IV Hình học 8 → Hình lăng trụ đứng và hình chóp đều

I. HÌNH LĂNG TRỤ ĐỨNG

1) Hình hộp chữ nhật: là hình hộp có 6 mặt là những hình chữ nhật (có 8 đỉnh, 6 mặt, 12 cạnh)

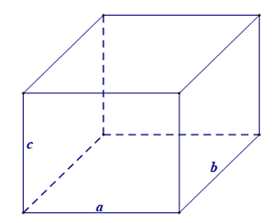
Diện tích xung quanh:

Sxq = 2(a + b)c

Diện tích toàn phần:

Stp= 2(ab + ac + bc)

Thể tích là: V = abc. Trong đó a, b là hai cạnh đáy, c là chiều cao

2) Hình lập phương: là một hình hộp chữ nhật có sáu mặt là những hình vuông.

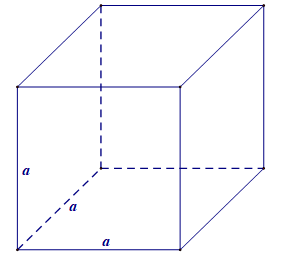
Diện tích xung quanh: Sxq = 4a²

Diện tích toàn phần: Stp = 6a²

Thể tích: V = a³

Trong đó có: a là cạnh của hình lập phương.

3) Hình lăng trụ đứng:

Hình lăng trụ đứng là hình học có những mặt bên là những hình chữ nhật (có diện tích có thẻ không bằng nhau), hai đáy là hai đa giác song song bằng nhau.

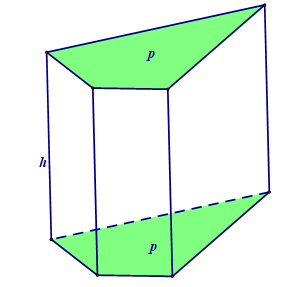
Diện tích xung quanh: Sxq = 2p.h

(p: nửa chu vi đáy, h: chiều cao)

Diện tích toàn phần: Stp = Sxq + 2Sđ

Thể tích: V = S.h (S là diện tích đáy)

II. HÌNH CHÓP ĐỀU

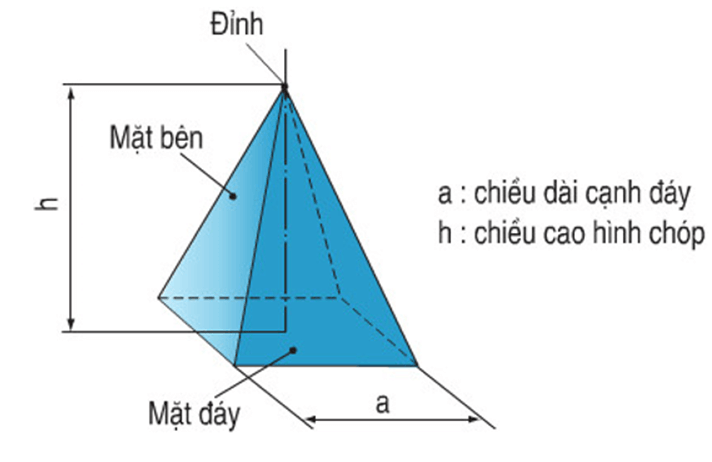
1) Hình chóp

– Hình chóp là hình học có mặt đáy là một đa giác, những mặt bên là những tam giác có cùng chung một đỉnh. Đỉnh này gọi là đỉnh của hình chóp

– Đường thẳng mà đi qua đỉnh chóp và vuông góc với mặt phẳng ở đáy thì được gọi là đường cao của hình chóp.

– Hình chóp mà có đáy là một tam giác được gọi là hình chóp tam giác.

– Hình chóp mà có đáy là một tứ giác được gọi là hình chóp tứ giác.

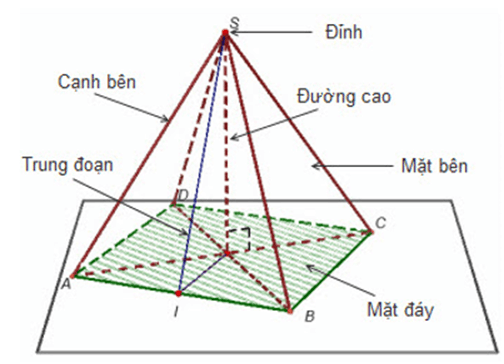
2) Hình chóp đều

– Hình chóp đều là hình chóp mà có mặt đáy là một hình đa giác đều, có mặt bên là những tam giác cân & bằng nhau có cùng chung một đỉnh.

Xét hình chóp đều S.ABCD dưới đây:

– H là chân của đường cao và đồng thời là tâm của đường tròn đi qua tất cả các đỉnh của mặt đáy.

– Đường cao được kẻ từ đỉnh S của mỗi mặt bên của hình chóp đều thì được gọi là trung đoạn của hình chóp ấy.

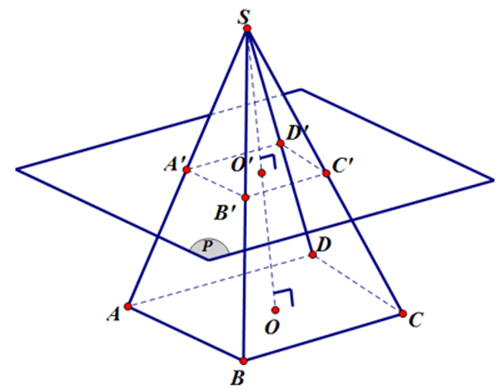
3) Hình chóp cụt đều

Cắt một hình chóp đều bằng một mặt phẳng song song với mặt phẳng đáy. Phần hình nằm giữa mặt phẳng đáy và mặt phẳng đó là một hình chóp cụt đều.

III. THỂ TÍCH, DIỆN TÍCH XUNG QUANH CỦA HÌNH CHÓP ĐỀU – HÌNH CHÓP CỤT ĐỀU.

Công thức để tính thể tích và diện tích:

– Kí hiệu là: p và p’ là nửa chu vi của các đáy.

– h là: chiều cao; và d là: trung đoạn.

– Sxq là: diện tích xung quanh

– Stp là: diện tích toàn phần

– B và B’ là: diện tích các đáy

– V là: thể tích.

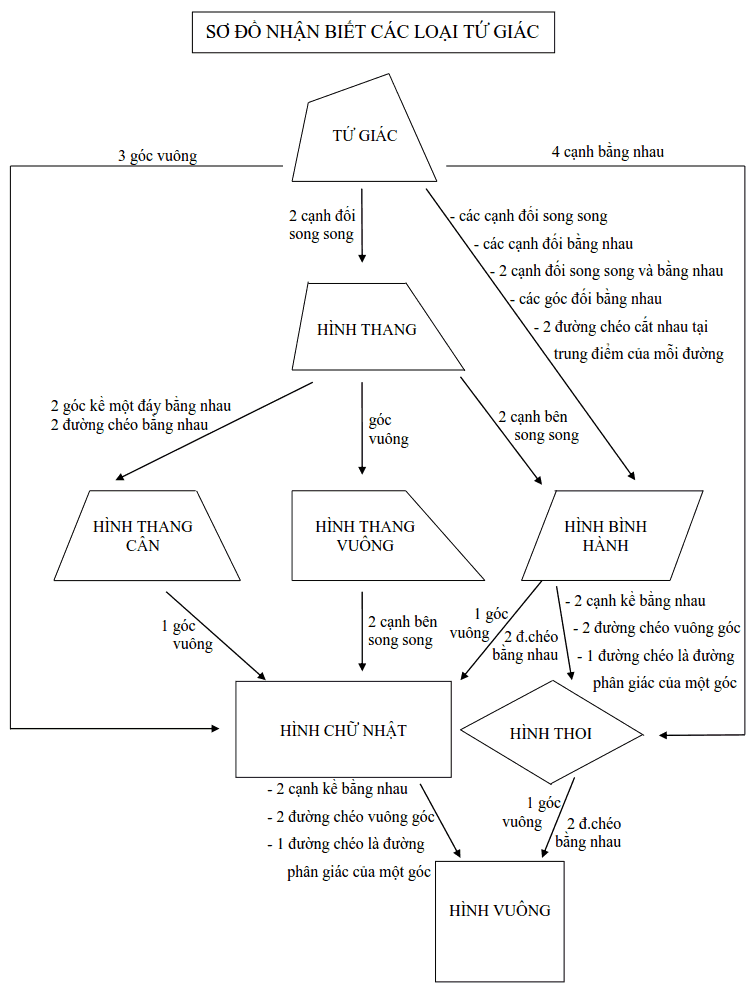
Sơ đồ nhận biết các loại tứ giác

B. DẠNG BÀI TẬP – ĐỀ CƯƠNG ÔN TẬP TOÁN 8 HỌC KÌ 2

I. PHẦN ĐẠI SỐ – TOÁN 8

A. Phương trình

Bài 1. Giải phương trình

a) 2x + 6 = 0

b) 4x + 20 = 0

c) 2(x+1) = 5x – 7

d) 2x – 3 = 0

e) 3x – 1 = x + 3

f) 15 – 7x = 9 – 3x

g) x – 3 = 18

h) 2x + 1 = 15 – 5x

i) 3x – 2 = 2x + 5

k) –4x + 8 = 0

l) 2x + 3 = 0

m) 4x + 5 = 3x

Bài 2: Giải phương trình

a) (x – 6)(x² – 4) = 0               b. (2x + 5)(4x² – 9) = 0                  c. (x – 2)²(x – 9) = 0

d) x² = 2x                                e. x² – 2x + 1 = 4                          f. (x² + 1)(x – 1) = 0

g) 4x² + 4x + 1 = 0                  h. x² – 5x + 6 = 0                           i. 2x² + 3x + 1 = 0

Bài 3. Giải các phương trình sau

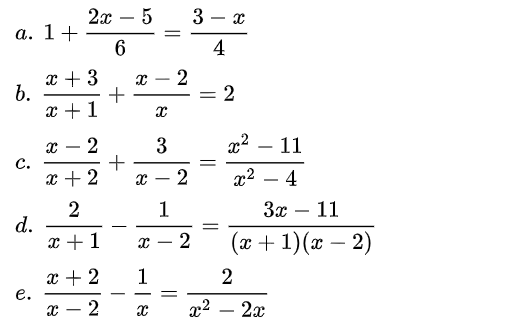
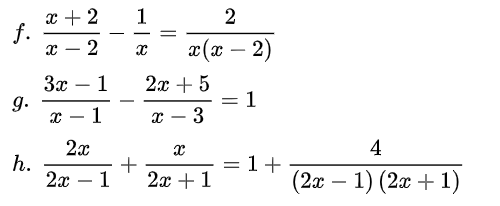
Bài 4. Giải phương trình:

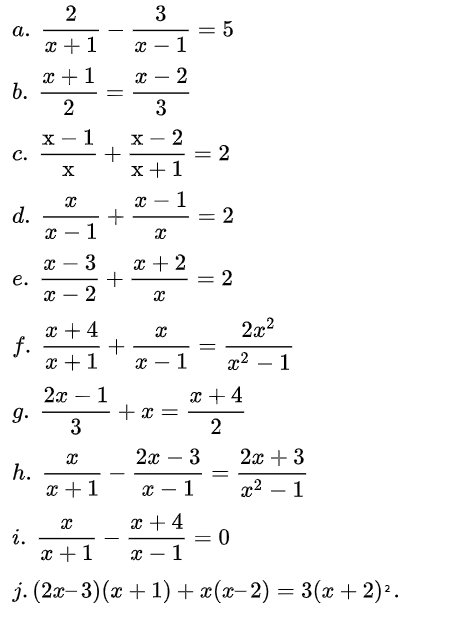
Bài 5. Giải các phương trình sau:

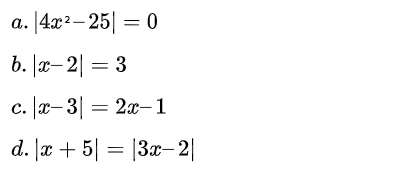
B. Bất phương trình

1) Cho a > b hãy chứng minh rằng: 5 – 2a < 5 – 2b

2) Giải những bất phương trình dưới sau đó biểu diễn tập hợp nghiệm ở trên trục số:

a) –4 + 2x < 0.

b) 2x – 3 ≥ 0

c) 2x + 5 ≤ 7

d) –2x – 1 < 5

e) 3x + 4 > 2x +3

f) 4x – 8 ≥ 3(3x – 1) – 2x + 1

d) 3x – (7x + 2) > 5x + 4

g) 3x – (7x + 2) > 5x + 4

h) 2x + 3(x – 2) < 5x – (2x – 4)

i)5x – (10x – 3) > 9 – 2x

k) x(x – 2) – (x + 1)(x + 2) < 12.

l) (2x – 3)(x + 4) < 2(x – 2)² + 2.

C. Giải bài toán bằng phương pháp lập phương trình

1) Tổng số học sinh của hai lớp 8C và 8D là 78 em. Nếu như chuyển 2 em từ lớp 8C qua lớp 8D thì số học sinh của hai lớp lúc này là bằng nhau. Tính số học sinh ban đầu của mỗi lớp.

2) Có 15 quyển vở bao gồm hai loại: loại I có giá 2000 đồng một quyển, loại II có giá 1500 đồng một quyển. Số tiền để mua được 15 quyển vở là 26000 đồng. Hỏi rằng có mấy quyển vở mỗi loại?

3) Hai thùng dầu C và D có tổng tất cả 100 lít. Nếu chuyển từ thùng C sang thùng D 18 lít thì số lượng dầu ở hai thùng là bằng nhau. Tính số lượng dầu lúc đầu ở mỗi thùng.

4) Tổng có 90 quyển chia làm hai chồng sách. Nếu ta chuyển từ chồng thứ nhất sang chồng thứ hai 10 quyển thì số sách ở chồng thứ hai sẽ gấp đôi chồng thứ nhất. Tính số sách ở mỗi chồng lúc khi ban đầu.

5) Một khu vườn hình chữ nhật có chu vi là khoảng 82m. Chiều dài hơn chiều rộng là khoảng 11m. Hãy tính diện tích khu vườn.

6) Một người đi bằng xe đạp xuất phát từ địa điểm A và đến địa điểm B với vận tốc là 15km/h và sau đó quay trở về từ vị trí B đến vị trí A với vận tốc là 12km/h. Cả lần đi lẫn lần về mất khoảng 4 giờ 30 phút. Hãy tìm chiều dài quãng đường.

7) Vào lúc 7 giờ, một chiếc ca nô xuôi dòng từ điểm A đến điểm B cách nhau 36km rồi ngay lập tức quay trở về bên điểm A lúc 11 giờ 30 phút. Hãy tìm vận tốc của ca nô khi xuôi dòng. Biết rằng vận tốc dòng nước chảy là 6km/h.

8) Một chiếc ca nô xuôi dòng từ bến đỗ A đến bến đỗ B mất 4 giờ, và ngược dòng từ bến đỗ B đến bến đỗ A mất 5h. Hãy tìm khoảng cách ở giữa hai bến, biết vận tốc của dòng nước này là 2km/h.

9) Một người đi xe đạp từ điểm A đến điểm B với vận tốc trung bình là 12km/h. Khi đi về từ điểm B đến điểm A, người đó đã đi với vận tốc trung bình là 10 km/h, nên thời gian lúc về nhiều hơn thời gian lúc đi là 15 phút. Hãy tìm độ dài của quãng đường AB.

10) Một người đi xe máy từ điểm A đến điểm B với vận tốc là 30 km/h. Đến điểm B người đó làm việc trong khoảng một giờ rồi quay trở về A với vận tốc là 24 km/h. Biết quãng thời gian tổng cộng là hết 5 giờ 30 phút. Hãy tính quãng đường AB.

11) Hiệu của hai số là bằng 50. Số này thì gấp ba lần số kia. Hãy tìm hai số đó.

12) Một bạn học sinh đi bộ đi học từ nhà cho đến trường với vận tốc trung bình là 4 km/h. Sau khi đi được 2 phần 3 (2/3) quãng đường bạn ấy đã tăng vận tốc đi lên là 5 km/h. Tính quãng đường đi từ nhà đến trường của bạn học sinh ấy, biết rằng quãng thời gian để bạn ấy đi từ nhà đến được trường là 28 phút.

13) Một chiếc xe ô tô đi từ điểm A đến điểm B là hết 3 giờ 12 phút. Nếu vận tốc của xe tăng thêm 10 km/h thì sẽ đến điểm B sớm hơn 32 phút. Hãy tính vận tốc ban đầu của xe và quãng đường AB.

14) Một người đi từ điểm A đến điểm B, nếu như đi bằng xe máy thì sẽ mất khoảng thời gian là 3 giờ 30 phút, còn nếu đi bằng ô tô thì sẽ mất khoảng thời gian là 2 giờ 30 phút. Hãy tính quãng đường AB, biết rằng vận tốc của ô tô lớn hơn vận tốc của xe máy là 20 km/h.

II. PHẦN HÌNH HỌC – TOÁN 8

Câu 1. Cho tam giác ABC vuông góc tại điểm A. Cạnh AB = 15cm, cạnh AC = 20cm. Vẽ tia Ax//BC, tia By vuông góc với cạnh BC tại điểm B, tia Ax giao tia By tại điểm D.

a) Chứng minh rằng ΔABC và ΔDAB động dạng với nhau

b) Tính DA, BC, DB.

c) AB giao CD tại điểm I. Tính diện tích của ΔBIC

Câu 2. Cho tam giác ABC như hình dưới, có đoạn AD là phân giác trong của góc CAB. Tìm x ở trong hình vẽ sau.

Câu 3. Cho một tam giác ABC vuông tại góc A có AC = 8cm; AB = 6 cm. Ở trên một nửa mặt phẳng bờ AC không có điểm B vẽ ra tia Ax song song với đoạn BC. Từ điểm C vẽ đoạn CD vuông góc với tia Ax tại điểm D.

a) Chứng minh hai tam giác ADC và tam giác CAB đồng dạng với nhau.

b) Tính DC.

c) Đoạn BD giao đoạn AC tại điểm I. Hãy tính diện tích của tam giác BIC.

Câu 4. Cho hình thang ABCD (có AB // CD) có góc DAB và góc DBC bằng nhau và AB = 5cm, AD = 3cm, BC = 4cm.

a) Chứng minh tam giác CBD và tam giác DAB đồng dạng với nhau.

b) Tính độ dài của 2 đoạn DB, DC.

c) Hãy tính diện tích của hình thang ABCD, biết rằng diện tích của tam giác ABD bằng 5cm².

Câu 5. Cho tam giác ABC vuông tại đỉnh A, có đường cao AD.

a) Tìm độ dài AH. Biết rằng AB = 6cm và AC = 8cm.

b) Chứng minh rằng: ΔABC và ΔDBA đồng dạng với nhau.

c) Chứng minh rằng: AB² = BC.BD.

Câu 6. Cho một hình chữ nhật có cạnh AB = 8cm; cạnh BC = 6cm.Vẽ một đường cao AH trong tam giác ADB.

a) Chứng minh rằng ΔAHB và ΔBCD đồng dạng với nhau.

b) Chứng minh ràng: AD² = DH.DB

c) Tính độ dài của hai đoạn thẳng DH và AH

Câu 7. Cho ΔABC vuông tại đỉnh A và có đường cao AH. Cho biết độ dài AB = 15cm, độ dài AH = 12cm.

a) Chứng minh rằng ΔAHB và ΔCHA đồng dạng với nhau.

b) Tính độ dài của đoạn thẳng HC; HB; AC.

c) Trên cạnh AC hãy lấy điểm E sao cho có CE = 5 cm; trên cạnh BC hãy lấy điểm F sao cho có CF = 4 cm. Chứng minh rằng ΔCEF vuông.

d) Chứng minh rằng: CE.CB = CF.CA.

Câu 8. Cho tam giác ABC có cạnh AB = 6cm, cạnh AC = 8 cm. Trên tia đối của cạnh AB lấy điểm D sao cho có: 3AD = AB. Kẻ đoạn DH vuông góc với cạnh BC.

a) Hãy chứng minh rằng: tam giác ABC và tam giác HBD đồng dạng với nhau.

b) Tính HB, BC, HD, HC

c) Gọi điểm K là giao điểm của đoạn DH và đoạn AC. Tính tỉ số diện tích giữa ΔAKD và ΔABC.

Câu 9. Cho ΔABC vuông tại đỉnh A có đoạn AB = 9cm; đoạn BC = 15cm. Lấy điểm M thuộc cạnh BC sao cho độ dài CM = 4cm, vẽ tia Mx vuông góc với đoạn BC và cắt AC tại điểm N.

a) Chứng minh ΔCMN và ΔCAB đồng dạng với nhau, suy ra được: CM.AB = MN.CA.

b) Tính MN.

c) Tính tỉ số giữa diện tích ΔCMN với diện tích ΔCAB.

Câu 10. Cho tam giác ABC vuông tại đỉnh A, có đoạn AB = 3cm, đoạn AC = 5cm, đường phân giác AD. Đường vuông góc với đoạn DC giao cạnh AC ở điểm E.

a) Chứng minh rằng tam giác CED và tam giác CBA đồng dạng với nhau.

b) Tính ra độ dài đoạn thẳng BC, đoạn thẳng BD

c) Tính độ dài AD

d) Tính diện tích của tam giác ABC và diện tích của tứ giác ABDE

Câu 11. Cho tam giác ABC cân tại đỉnh A. Vẽ đường cao BH và đường cao CK (H nằm trên AC, K nằm trên AB)

a) Chứng minh tam giác CAB đồng dạng với ΔCHB. Tính tỉ số đồng dạng.

b) Chứng minh KH // BC

c) Cho biết AB = AC = b, BC = a. Tính độ dài của đoạn thẳng HK theo b và a.

C. ĐỀ THI HỌC KÌ 2 TOÁN 8 (CÓ ĐÁP ÁN)

Trên đây là bài viết Đề cương ôn thi học kì 2 toán 8 mới nhất dành cho các em học sinh khối 8, đang chuẩn bị bước vào kỳ thi cuối kỳ đầy thử thách. Các em tham khảo bài viết, tìm thêm nhiều dạng đề nữa luyện tập nhé. Chúc các em đạt được điểm thật cao nhé!