Hình nón là một loại hình học không gian các em học sinh sẽ bắt đầu làm quen từ lớp 9. Những về hình học không gian nói chung không phải là dễ dàng đối với các em. Nếu không nắm rõ kiến thức và khái niệm về hình nón, đến khi làm bài tập các em sẽ không thể hiểu được. Sau đây, sẽ là một vài bài tập hình nón được HOCMAI tổng hợp, các em tham khảo nhé!
I. Lý thuyết cơ bản về hình nón
1. Khái niệm về hình nón
Hình nón (hay còn gọi là khối nón, khối tròn xoay) hiểu đơn nhất là hình được tạo ra khi quay một tam giác vuông một vòng quanh một cạnh góc vuông cố định.
Hình minh họa:
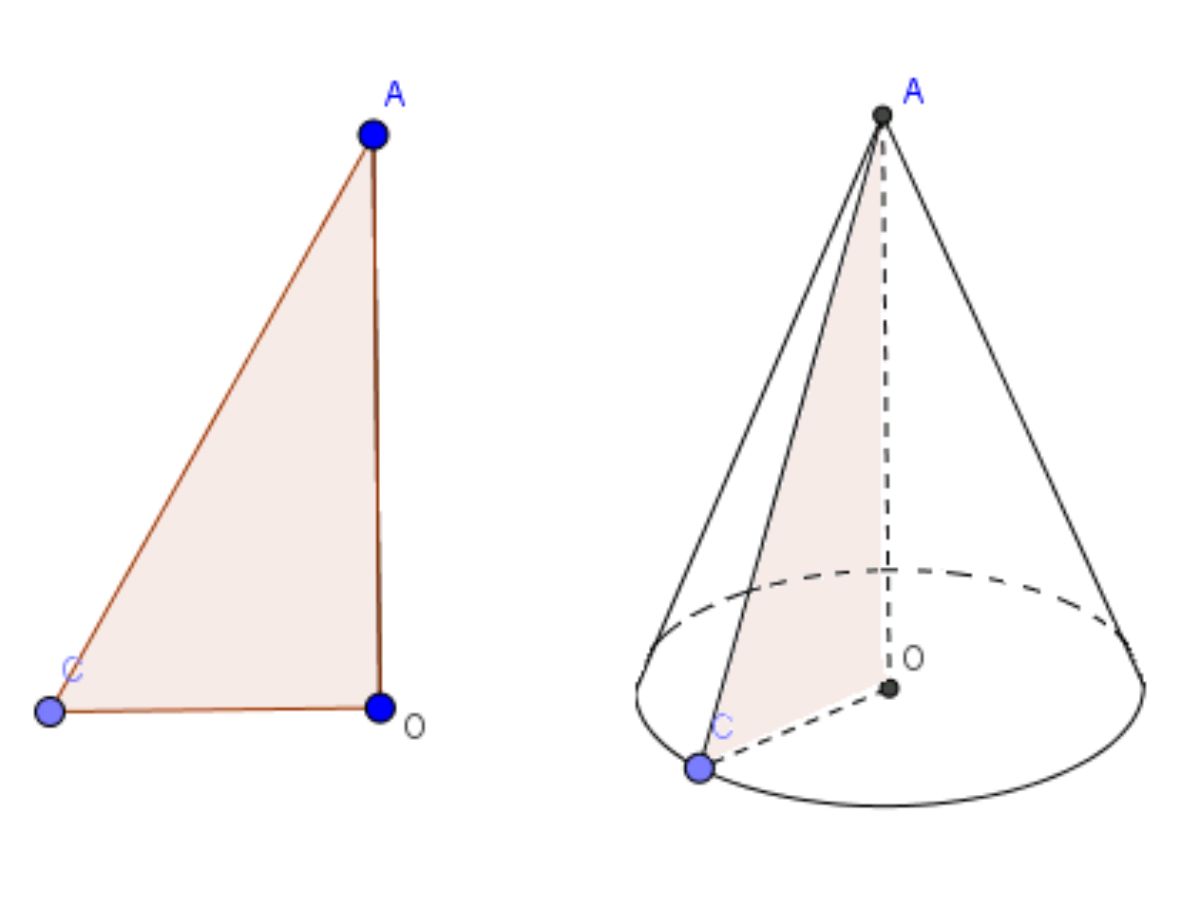
Để hiểu rõ chi tiết kiến thức chi tiết về hình nón, các em có thể tham khảo Hình nón là gì?
2. Công thức hình nón
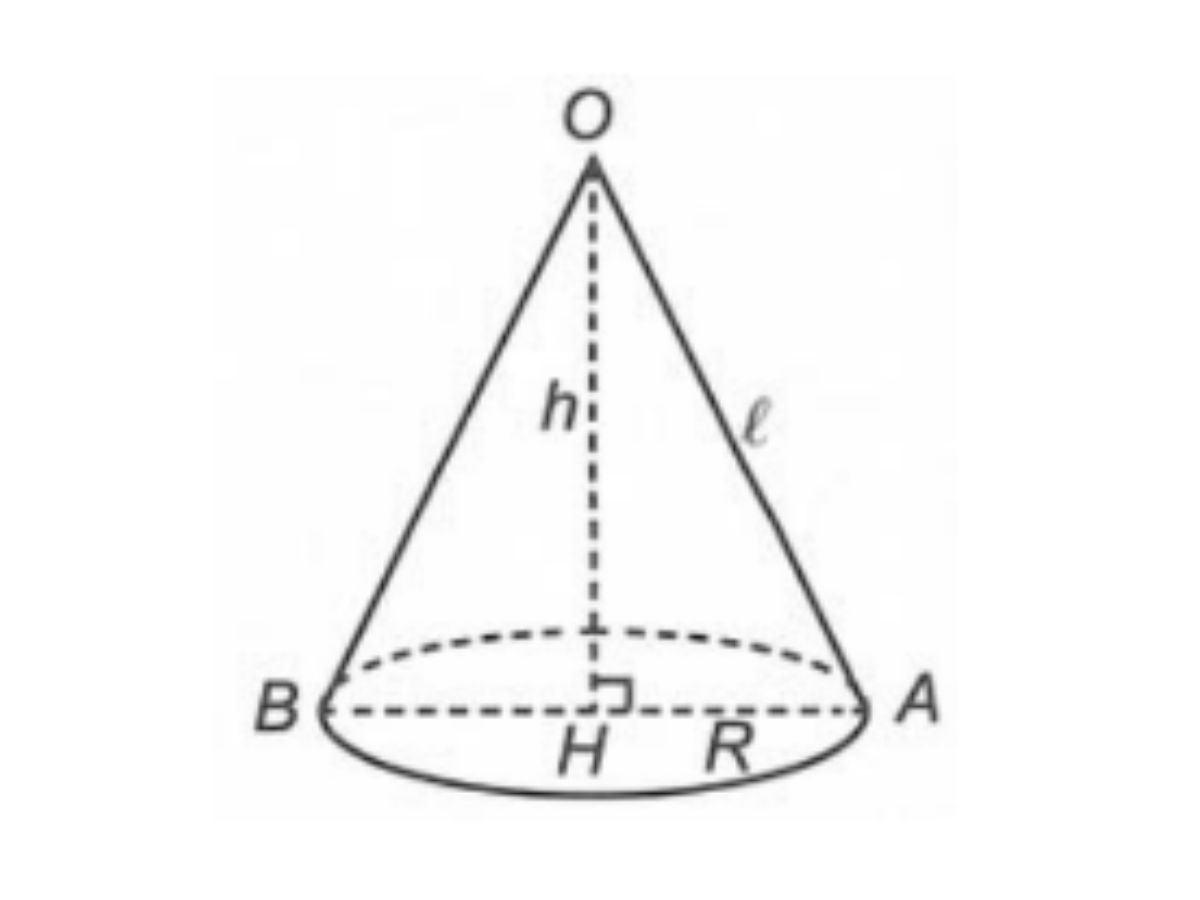
Đường cao: h
Bán kính đáy: r
Đường sinh: l
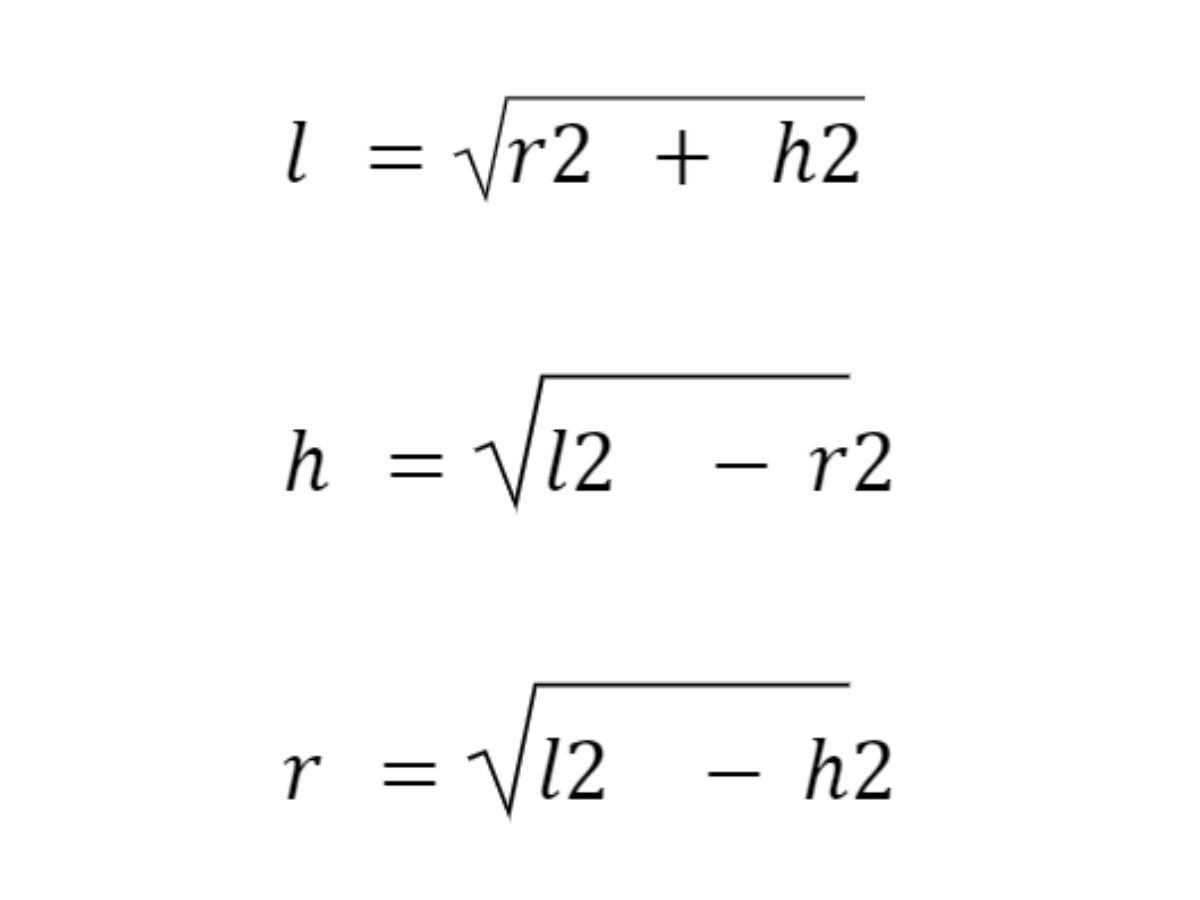
Diện tích xung quanh hình nón
SXQ = Π.R.L
Trong đó:
- Sxq: diện tích xung quanh
- π: hằng số Pi, với Pi 3,14
- r: bán kính đáy hình nón
- l: đường sinh hình nón (SB trong hình minh họa là đường sinh)
Diện tích toàn phần hình nón
STP = SXQ + SĐ = Π.R.L + Π.R^2
Trong đó:
- Stp: diện tích toàn phần
- Sxq: diện tích xung quanh
- Sđ: diện tích đáy
- Π: hằng số Pi, với Pi3,14
- r: bán kính đáy hình nón
- l: đường sinh hình nón
Thể tích hình nón
V= 1/3.Π.R^2.H
Trong đó:
- V là thể tích hình nón
- π là hằng số Pi, với Pi xấp xỉ bằng 3,14
- r là bán kính đáy hình nón
- h là đường cao hình nón
II. Bài tập về hình nón
Bài 1:Tính diện tích xung quanh của khối nón có thiết diện qua trục là tam giác vuông cân diện tích bằng 2?
- S = 2√2π
- S = 4π
- S = 2π
- S = 4√2π
Hướng dẫn giải:
Tam giác OAB vuông cân, diện tích tam giác OAB bằng 2
1/2 OA^2 = 2
OA = OB = 2
AB = √(2^2 +2^2) = 2√2
h = R = AB/2 = √2
Suy ra Sxq = 2√2π
Vậy đáp án đúng là: A
Bài 2: Hình nón có đường sinh l = 2a và hợp với góc đáy bằng 60 độ. Hình nón có diện tích toàn phần bằng bao nhiêu?
- 4πa^2
- 3πa^2
- 2πa^2
- πa^2

Hướng dẫn giải:
Theo giả thiết:
SA = 1 = 2a vào góc SAO = 60 độ
Suy ra: R = OA = SA.cos60 = a
Stp = πRl + πR^2 = 3πa^2
Vậy đáp án đúng là: B
Bài 3: Tính diện tích xung quanh của một hình nón, biết rằng hình nón đỉnh S có bán kính đáy R = a√2, góc có đỉnh bằng 60 độ.
- 4πa^2
- 3πa^2
- 2πa^2
- πa^2
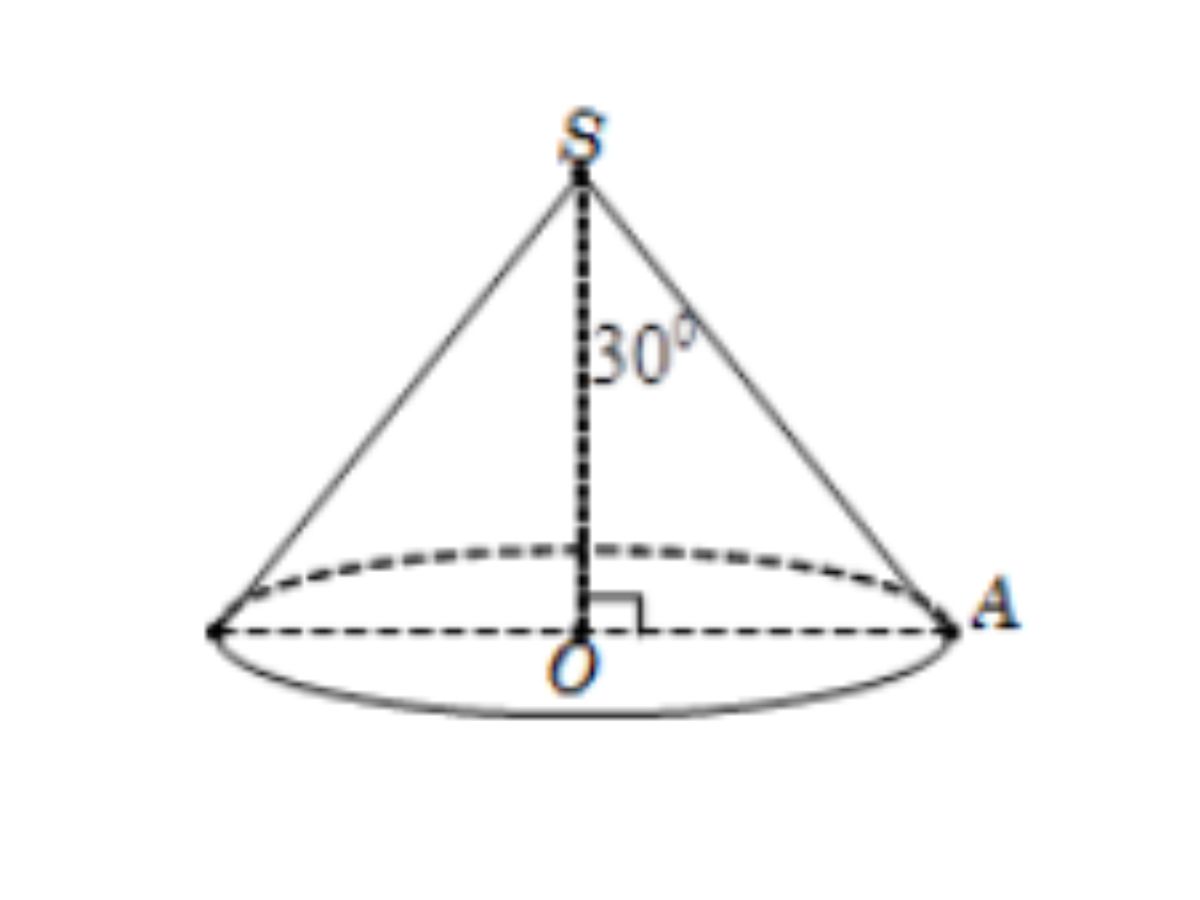
Hướng dẫn giải:
Theo giả thiết:
OA = a√2 vào góc OSA = 30 độ
Suy ra, độ dài đường sinh là:
L = SA = OA/sin30 = 2a√2
Vậy diện tích xung quanh bằng:
Sxq = πRl = 4πa^2
Vậy đáp án đúng là: A
Bài 4: Trong không gian, cho tam giác ABC vuông tại A, AB = a và AC = a√3. Tam giác ABC quay quanh trục AB sẽ tạo ra một hình nón. Tính đường sinh l của hình nón đó.
- 1 = a
- 1 = a√2
- 1 = a√3
- 1 = 2a
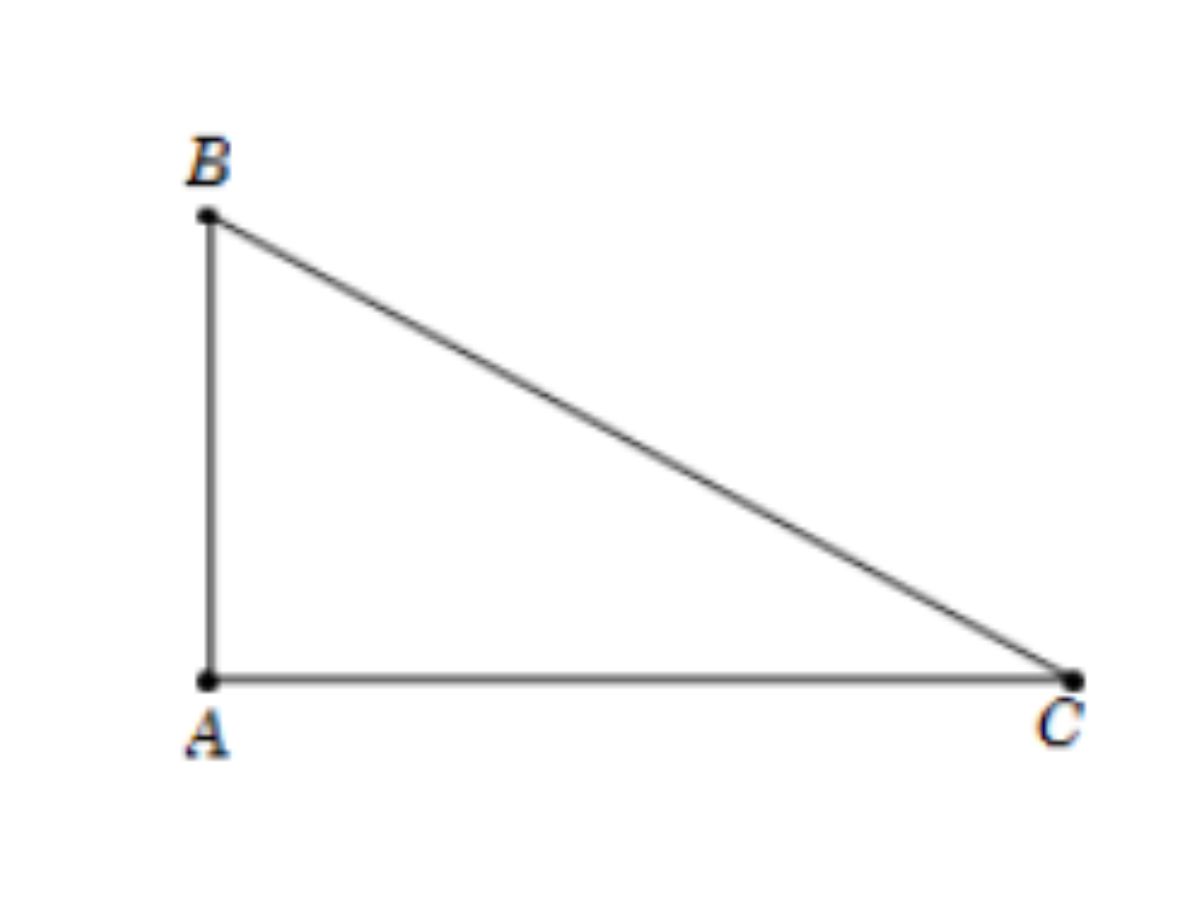
Hướng dẫn giải:
Từ giả thiết ta có hình nón có đỉnh B, tâm đường tròn đáy là A, bán kính đáy là AC = a√3 và chiều cao hình nón là AB = a
Suy ra độ dài đường sinh của hình nón là:
1 = BC = √(AB^2 + AC ^2) = 2a
Vậy đáp án đúng là: D
Bài 5: Cạnh bên của một hình nón bằng 2a. Thiết diện qua trục của nó là một tam giác cân có góc ở đỉnh bằng 120 độ. Tính Stp của hình nón.
- π(3 + √3)
- 2πa^2(3 + √3)
- 6πa^2
- πa^2(3 + 2√3)
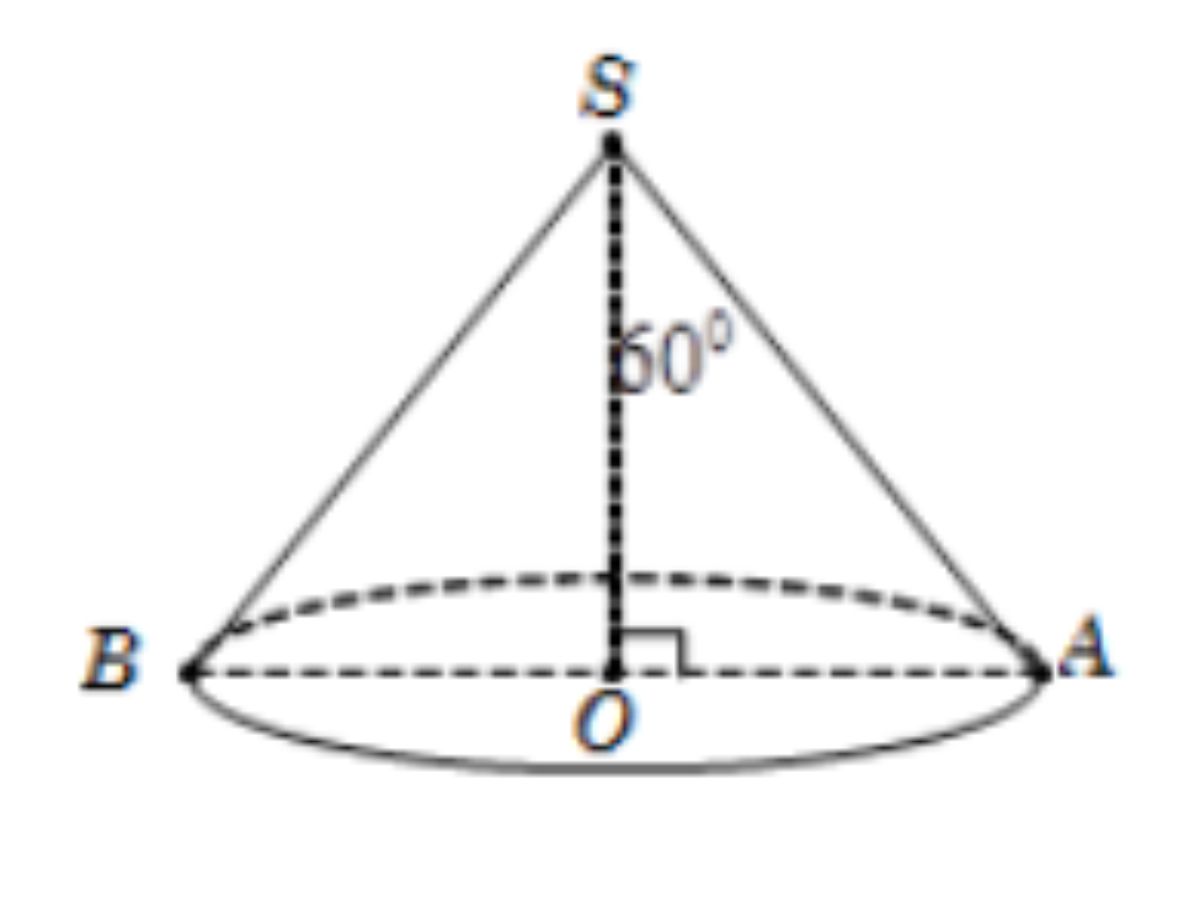
Hướng dẫn giải:
Ta đặt: Đỉnh S, tâm của đáy là O, thiết diện qua trục là SAB. Theo giả thiết, ta có SA = 2a và góc ASO = 60 độ.
Vì tam giác SAO vuông tại O nên ta có:
OA = SA.sin60 = a√3
Vậy diện tích toàn phần:
Stp = πRl + πR^2 = πOA.SA + πOA^2 = πa^2(3 + 2√3)
Vậy đáp án đúng là: D
Bài 6: Cho mặt cầu tâm O, bán kính R = a. Cho một hình nón có đỉnh là S ở trên mặt cầu, đáy là đường tròn tương giao của mặt cầu đó với mặt phẳng vuông góc với đường thẳng SO tại H sao cho đoạn SH = 3a/2. Đường sinh l của hình nón dài bao nhiêu?
- 1 = a
- 1 = a√2
- 1 = a√3
- 1 = 2a
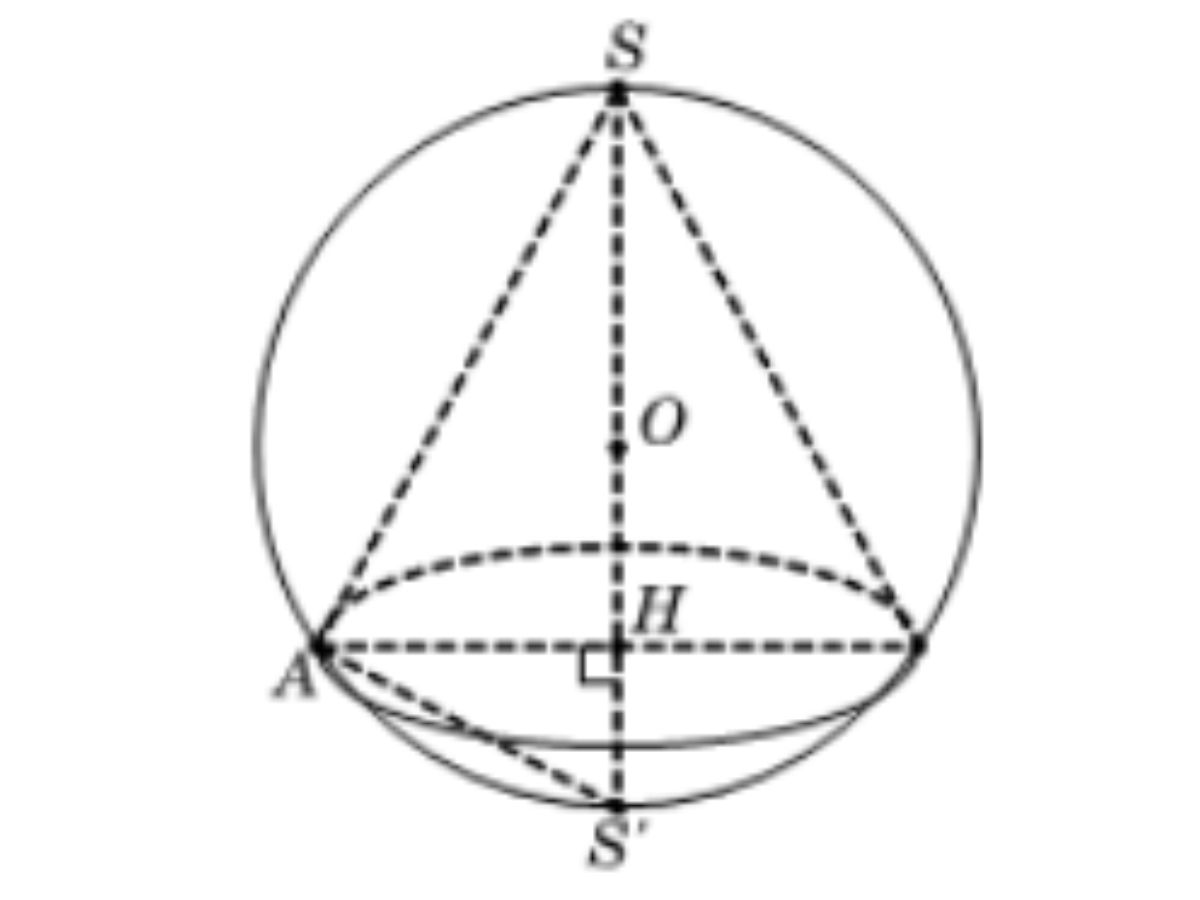
Hướng dẫn giải:
Gọi điểm đối xứng của S qua tâm O là S’, điểm bất kỳ trên đường tròn đáy của hình nón là A.
Tam giác SAS’ có góc SAS’ bằng 90 độ và đường cao AH nên: SA^2 = SH.SS’
Suy ra SA = a√3
Vậy đáp án đúng là: C
Bài 7: Cho hình nón có đỉnh S, đường cao SO = h, đường sinh SA. Cho hình chóp nội tiếp hình nón, có đỉnh S và đáy là hình vuông ABCD cạnh a. Tính tan của nửa góc ở đỉnh của hình nón.
- (h√2)/2a
- (a√2)/2h
- (a√2)/h
- (h√2)/a
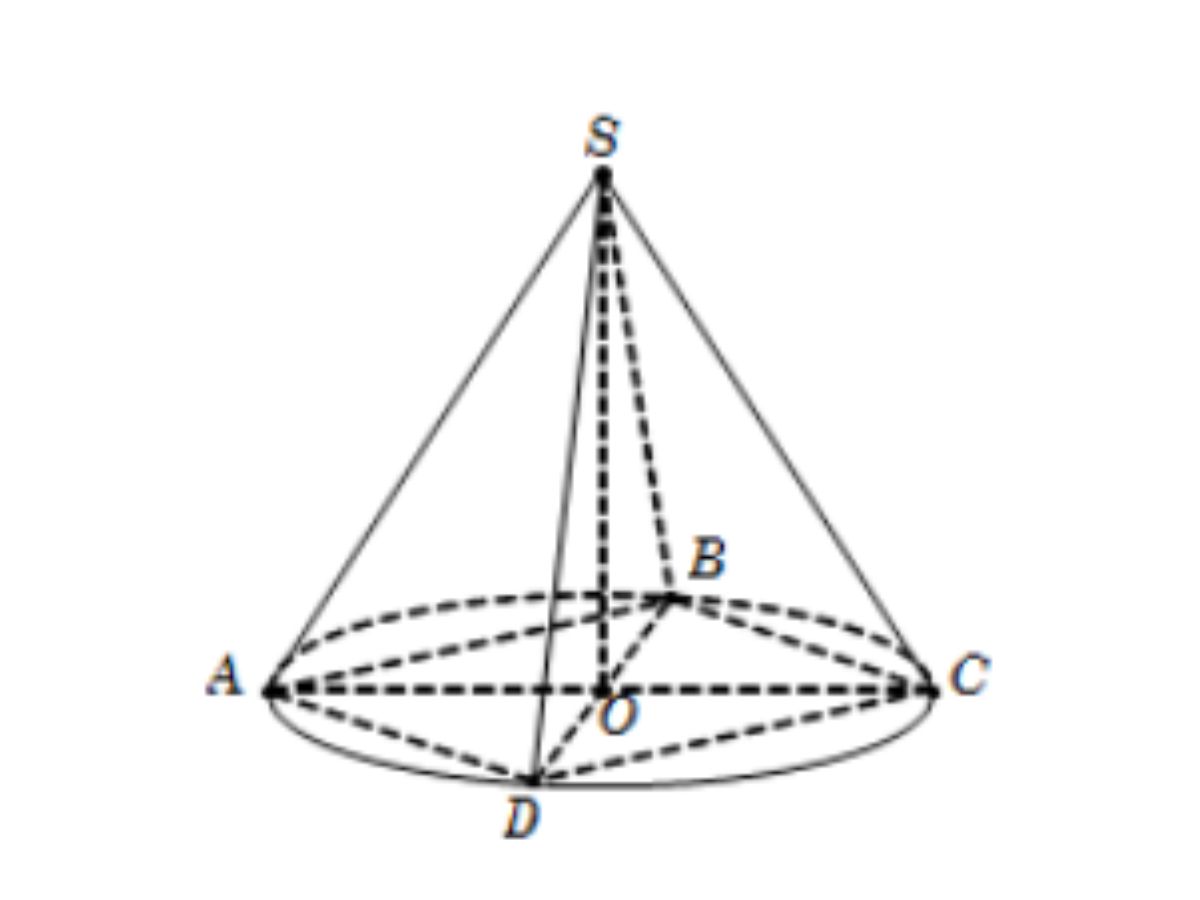
Hướng dẫn giải:
Nửa góc ở đỉnh của hình nón là góc ASO, hình vuông ABCD cạnh a.
Suy ra OA = (a√2)/2
tanASO = OA/SO = (a√2)/2h
Vậy đáp án đúng là B
Bài 8:
Đặt một hình nón vào một hình lập phương (cạnh của hình lập phương bằng 1) (hình 93). Tính:
- a) Bán kính đáy của hình nón.
- b) Độ dài đường sinh.
Hướng dẫn giải:

Vậy độ dài bán kính đáy hình nón bằng 1/2 và độ dài đường sinh là √5/2
Một số kiến thức về hình học không gian khác mà các em có thể tham khảo:
Vậy là đã kết thúc chuỗi bài tập hình nón rồi, các em học sinh đã nhớ được hết công thức của hình nón và làm bài tập nhuần nhuyễn chưa nhỉ? HOCMAI mong rằng các em không ngừng nỗ lực trong học tập để không phụ lòng bố mẹ và thầy cô nhé. Để tham khảo thêm kiến thức bổ ích, các em có thể truy cập hoctot.hocmai.vn





















